если размер препятствия меньше чем длина волны то
Если размер препятствия меньше чем длина волны то
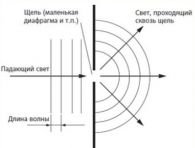
Мы ежедневно сталкиваемся с дифракцией радиоволн, слушая радиопередачи и пользуясь сотовым телефоном. Дифракция приводит к огибанию электромагнитными волнами препятствий и проникновению их в область геометрической тени. Из-за дифракции тень от препятствия с прямым краем не бывает идеально резкой: при освещении непрозрачных экранов источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдаются чередующиеся светлые и темные дифракционные полосы (рис. 3.1). Если на пути параллельного светового пучка расположено круглое препятствие, например, диск, шарик, круглое отверстие в непрозрачном экране, то на экране, расположенном на большом расстоянии от препятствия, появляется дифракционная картина в виде чередующихся светлых и темных колец.
Дифракция волн существенно зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию.
Наиболее отчетливо дифракция обнаруживается в тех случаях, когда размер огибаемых препятствий соизмерим с длиной волны. Поэтому легко наблюдается дифракция звуковых, сейсмических и радиоволн, для которых длина волны лежит в пределах от нескольких метров до нескольких километров. Значительно труднее наблюдать дифракцию электромагнитных волн оптического диапазона, длины которых лежат в пределах 
Явление дифракции нагляднее всего демонстрируется с помощью волн на поверхности воды. Если размер отверстия или препятствия заметно меньше длины волны, то волна с ним не взаимодействует. Этим обусловлено то, что в шторм волны не проникают в бухту с узким входом. Морские волны длиннее, чем вход в бухту, и не замечают этого входа. Толщина стволов деревьев, стоящих в воде, меньше длины волны, и волны не взаимодействуют с ними (рис. 3.2).
А если размеры препятствия много больше длины волны, то волны за него не проникают, создается область тени: световая тень (рис. 3.3), звуковая тень, ограничения при передаче телевизионного сигнала, невозмущенная поверхность воды за большим валуном (рис. 3.4).
Из-за малости длины волны дифракционные явления в оптике наблюдать сложнее, чем в механике, но их проявления более многообразны и красочны.
Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, называют дифракцией волн.
В строгой постановке дифракционные задачи, ввиду их сложности, допускают аналитические решения лишь в простейших идеализированных случаях. В оптике значительно большее значение имеют приближенные методы решения дифракционных задач, основанные на принципе Гюйгенса в обобщенной формулировке Френеля.
Если размер препятствия меньше чем длина волны то
Нередко волна встречает на своем пути небольшие (по сравнению с длиной волны) препятствия, которые она способна огибать.
Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними.
Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней.
За камнем волны распространяются так, как если бы его не было совсем.
Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (наприер, большого камня) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны.
Вы можете слышать сигнал машины за углом дома, когда самой машины не видно.
В лесу деревья заслоняют ваших товарищей.
Чтобы их не потерять или не потеряться самому, вы начинаете кричать.
Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей.
Отклонение от прямолинейного распространения волн, или огибание волнами препятствий — называется дифракцией.
Дифракция присуща любому волновому процессу, так же как и интерференция.
При дифракции происходит искривление волновых поверхностей у краев препятствий.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
Явление дифракции волн на поверхности воды можно наблюдать, если, например, поставить на пути волн экран с узкой щелью, размеры которой меньше длины волны.
В этом опыте хорошо бывает видно, что за экраном распространяется круговая волна, как если бы в отверстии экрана находилось колеблющееся тело — источник волн.
Согласно принципу Гюйгенса так и должно быть.
Вторичные источники в узкой щели располагаются столь близко друг к другу, что их можно рассматривать как один точечный источник.
Если же размеры щели велики по сравнению с длиной волны, то картина распространения волн за экраном совершенно иная.
Волна проходит сквозь щель, почти не меняя своей формы.
По краям можно заметить искривления волновой поверхности, в результате чего волна частично проникает и в пространство за экраном.
Принцип Гюйгенса позволяет понять, почему происходит дифракция.
Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
Помогите решить тест по физике срочно.
1. Явление зависимости показателя преломления от цвета световой волны, называют…
А. дисперсией Б. интерференцией В. Дифракцией Г. Поляризацией
2. Определите, что будет наблюдаться в точке А при интерференции света, если разность хода равна 2мкм, а длина волны 780нм. Чему равна k?
А. k = 2.6,min Б. k = 3,max В. k = 2, min Г. k = 2.6, max
3. Если размер препятствия меньше, чем длина волны, то…
А. волна проходит без изменения Б. форма волны и длина волны изменяются
В. Форма волны изменяется, а длина волны – нет Г. Форма не изменяется, а длина-да
4. При прохождении стеклянной призмы белый свет…
А. остается без изменений Б. разлагается на спектр
5. Дифракционная решетка имеет период 1/100. Определить длину волны, если угол отклонения для второго максимума составляет 60.
А. 823нм Б. 500нм В. 523нм Г. 698нм
6. При дисперсии света наиболее отклоняются…
А. фиолетовые лучи Б. зеленые лучи В. желтые лучи Г. Красные лучи
8. При сложении волн в пространстве, наблюдается…
А. сплошная цветная полоса Б. сплошная черная полоса
В. чередование цветных и черных полос
9. Сложную структуру имеет…
А. белый свет Б. красный свет В. зеленый свет Г. Фиолетовый свет
10. Дифракционную картину для световых волн можно получить, если…
А. взять две лампы накаливания Б. разделить источник света на два
В. разделить волну на две
11. Самым первым описал интерференцию на тонких пленках…
А. Гюйгенс Б. Френель В. Максвелл Г. Юнг Д. Ньютон
1. Человек ростом 2м стоит около столба с фонарем, висящего на высоте 5м. При этом он отбрасывает тень длиной 1,2 м. На какое расстояние удалится человек от столба, если длина его тени стала 2м
2. Угол падения луча на поверхность масла 600, а угол преломления 360. Найдите показатель преломления масла
Если размер препятствия меньше чем длина волны то
Часто волна встречает на своем пути небольшие (по сравнению с ее длиной) препятствия. Соотношение между длиной волны и размером препятствий определяет в основном поведение волны.
Волны способны огибать края препятствий. Когда размеры препятствий малы, волны, огибая края препятствий, смыкаются за ними. Так, морские волны свободно огибают выступающий из воды камень, если его размеры меньше длины волны или сравнимы с ней. За камнем волны распространяются так, как если бы его не было совсем (маленькие камни на рис. 127). Точно так же волна от брошенного в пруд камня огибает торчащий из воды прутик. Только за препятствием большого по сравнению с длиной волны размера (большой камень на рис. 127) образуется «тень»: волны за него не проникают.
Способностью огибать препятствия обладают и звуковые волны. Вы можете слышать сигнал машины за углом дома, когда самой машины не видно. В лесу деревья заслоняют ваших товарищей. Чтобы их не потерять, вы начинаете кричать. Звуковые волны в отличие от света свободно огибают стволы деревьев и доносят ваш голос до товарищей. Отклонение от прямолинейного распространения волн, огибание волнами препятствий, называется дифракцией. Дифракция присуща любому волновому процессу в той же мере, как и интерференция. При дифракции происходит искривление волновых поверхностей у краев препятствий.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней.
ДИФРАКЦИЯ СВЕТА
Если свет представляет собой волновой процесс, то, кроме интерференции, должна наблюдаться и дифракция света. Ведь дифракция — огибание волнами препятствий — присуща любому волновому движению. Но наблюдать дифракцию света нелегко. Дело в том, что волны заметным образом огибают препятствия, размеры которых сравнимы с длиной волны, а длина световой волны очень мала.
Пропуская тонкий пучок света через маленькое отверстие, можно наблюдать нарушение закона прямолинейного распространения света. Светлое пятно против отверстия будет большего размера, чем это следует ожидать при прямолинейном распространении света.
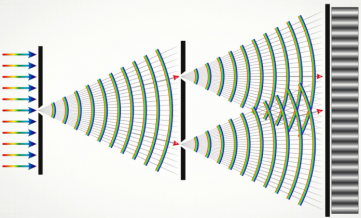
Опыт Юнга. В 1802 г. Юнг, открывший интерференцию света, поставил классический опыт по дифракции (рис. 203). В непрозрачной ширме он проколол булавкой два маленьких отверстия В и С на небольшом расстоянии друг от друга.
Эти отверстия освещались узким световым пучком, прошедшим в свою очередь через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, решила успех опыта. Интерферируют только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции из отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции световых волн на экране появлялись чередующиеся светлые и темные полосы. Закрывая одно из отверстий, Юнг обнаруживал, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые Юнгом были измерены длины волн, соответствующие световым лучам разного цвета, причем весьма точно.
Теория Френеля. Исследование дифракции получило свое завершение в работах Френеля. Френель не только более детально исследовал различные случаи дифракции на опыте, но и построил количественную теорию дифракции, позволяющую в принципе рассчитать дифракционную картину, возникающую при огибании светом любых препятствий. Им же было впервые объяснено прямолинейное распространение света в однородной среде на основе волновой теории.
Этих успехов Френель добился, объединив принцип Гюйгенса с идеей интерференции вторичных волн. Об этом кратко уже упоминалось в четвертой главе.
Для того чтобы вычислить амплитуду световой волны в любой точке пространства, надо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке пространства.
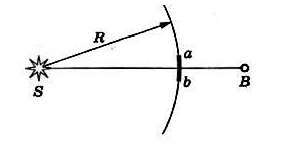
Такого рода расчеты позволили понять, каким образом свет от точечного источника S, испускающего сферические волны, достигает произвольной точки пространства В (рис. 204).
Если рассмотреть вторичные источники на сферической волновой поверхности радиусе R. то результат интерференции вторичных волн от этих источников в точке В оказывается таким, как если бы лишь вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, испущенные источниками, расположенными на остальной части поверхности, гасят друг друга в(результате интерференции. Поэтому все происходит так, как если бы свет распространялся лишь вдоль прямой SB, т. е. прямолинейно.
Одновременно Френель рассмотрел количественно дифракцию на различного рода препятствиях.
Любопытный случай произошел на заседании Французской Академии наук в 1818 г. Один из ученых, присутствовавших на заседании, обратил внимание на то, что теории Френеля вытекают факты, явно противоречащие здравому смыслу. При определенных размерах отверстия и определенных расстояниях от отверстия до источника света и экрана в центре светлого пятна должно находиться темное пятнышко. За маленьким непрозрачным диском, наоборот, должно находиться светлое пятно в центре тени. Каково же было удивление ученых, когда поставленные эксперименты доказали, что так и есть на самом деле.
Дифракционные картины от различных препятствий. Из-за того, что длина световой волны очень мала, угол отклонения света от направления прямолинейного распространения невелик. Поэтому для отчетливого наблюдения дифракции (в частности, в тех случаях, о которых только что говорилось) расстояние между препятствием, которое огибается светом, и экраном должно быть велико.
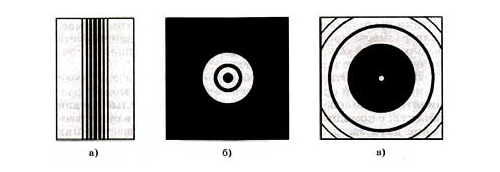
На рисунке 205 показано, как выглядят на фотографиях дифракционные картины от различных препятствий: а) тонкой проволочки; б) круглого отверстия; в) круглого экрана.
Зоны Френеля для трехсантиметровой волны
Зонная пластинка для трехсантиметровых волн
Дифракция света
теория по физике 🧲 оптика
Дифракция — явление, присущее всем волновым процессам подобно интерференции. Чтобы лучше понять, в чем заключается явление дифракции света, сначала рассмотрим дифракцию механических волн.
Дифракция механических волн
Иногда на пути волны встречаются препятствия разных размеров. Если препятствия небольшие, волны легко их огибают и смыкаются за ними. Поэтому морские волны свободно огибают выглядывающие из воды камни и распространяются за ними так, как если бы их не было совсем. Если размер препятствия больше длины волны, за ним образуется «тень» — область, в которую волны проникнуть не могут.
На рисунке ниже видно, что за мелкими камнями волны распространяются так же, как если бы их не было. Но за большой глыбой поверхность воды спокойная — волны в эту область не проникают.
Внимание! Малыми препятствиями будем считать те, размеры которых намного меньше длины распространяющейся волны или сравнимы с ней.
Способность волн огибать препятствия является следствием отклонения распространения волн от их прямолинейного распространения. Такой способностью обладают не только волны на поверхности воды, но и звуковые волны. Вы услышите, как сигналит автомобиль за домом, который стоит между ним и вами препятствием именно благодаря дифракции. Звуковая волна обогнет дом и продолжит распространяться за ним. По этой же причине в лесу так далеко распространяется клик «Ау!» — деревья для звуковой волны не являются серьезным препятствием, и она их легко огибает.
Дифракция — явление отклонения от прямолинейного распространения волн.
Дифракция волн проявляется особенно отчетливо в случаях, когда размеры препятствий меньше длины волны или сравнимы с ней. Это явление встречается в природе, но его также можно вызвать искусственно. К примеру, дифракцию волн на поверхности воды можно наблюдать, налив воду в ванночку и поставив на пути возбуждаемых волн искусственное препятствие.
Если на пути распространения волн поставить экран с узкой щелью, размеры которой меньше длины волны, то увидим, что за ней начинает распространяться круговая волна. Такая же волна получилась, если бы в щели экрана находилось колеблющееся тело — источник волн.
Если же на пути распространения волны поставить экран с широкой щелью, за ним будет распространяться волна почти такой же формы. Волновая поверхность в этом случае искривляется только по краям щели.
Понять, почему появляется явление дифракции волн, помогает принцип Гюйгенса. Согласно ему, каждая точка волновой поверхности является источником вторичных волн. Вторичные волны, испускаемые участками среды, проникают за края препятствия, расположенного на пути распространения волны.
Дифракция световых волн
Если свет — это волна, то ему тоже должно быть присуще явление дифракции. Однако наблюдать дифракцию света сложно. Ведь дифракцию можно наблюдать тогда, когда препятствие сравнимо с длиной волны или меньше ее. А длина световой волны очень мала. Поэтому чтобы наблюдать дифракцию света, нужны очень малые препятствия.
Дифракция света на узкой щели
Наблюдать отклонение от прямолинейного распространения света можно, если пропустить пучок световых волн через узкую щель. При этом светлое пятно на экране будет больше, чем сама щель. Это возможно только в случае, если свет отклоняется от своего прямолинейного распространения.
Опыт Юнга
В 1802 г. Т. Юнг, который открыл интерференцию света, поставил классический опыт по наблюдению дифракции. В непрозрачной ширме он проколол булавкой два небольших отверстия В и С на малом расстоянии друг от друга. Эти отверстия он осветил узким световым пучком, прошедшим через малое отверстие А в другой ширме. Именно эта деталь, до которой очень трудно было додуматься в то время, определила успех эксперимента. Интерферируют ведь только когерентные волны. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия А вызвала в отверстиях В и С образование когерентных источников световых волн. Вследствие дифракции от отверстий В и С выходили два световых конуса, которые частично перекрывались. В результате интерференции этих двух световых волн на экране появлялись картина, состоящая из чередующихся светлых и темных полос.
Закрыв одно из отверстий, Юнг обнаружил, что интерференционные полосы исчезали. Именно с помощью этого опыта впервые ученый измерил длины волн, соответствующие световым лучам разного цвета. И ему удалось сделать это с высокой точностью.
Принцип Гюйгенса — Френеля
Исследование дифракции завершил французский ученый О. Френель. Он занимался детальным исследованием различных случаев дифракции, что позволило ему разработать количественную теорию дифракции. Она помогла физику получить точные расчеты дифракционной картины, которая возникала при огибании светом различных препятствий. Френелю также удалось впервые объяснить, почему в однородной среде свет распространяется прямолинейно.
Успех Френеля объясняется тем, что он стал первым, кто решил объединить принцип Гюйгенса с идеей интерференции вторичных волн. В результате зародилась теория, которая получила название принципа Гюйгенса — Френеля:
Волновая поверхность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции.
Чтобы вычислить амплитуду световой волны в любой точке пространства, необходимо мысленно окружить источник света замкнутой поверхностью. Интерференция волн от вторичных источников, расположенных на этой поверхности, определяет амплитуду колебаний в рассматриваемой точке пространства. Такие расчеты дали объяснение тому, как свет от точечного источника S, являющегося источником сферических волн, достигает любой точки В пространства.
Если рассмотреть вторичные источники на сферической волновой поверхности радиусом R, то результат сложения вторичных волн от этих источников в точке В оказывается таким, как если бы только вторичные источники на малом сферическом сегменте ab посылали свет в точку В. Вторичные волны, распространяющие от источников, расположенных на остальной части поверхности, гасят друг друга в результате сложения. Поэтому все происходит так, как если бы свет распространялся вдоль прямой SB, т. е. прямолинейно. Эта теория Френеля доказала закон прямолинейного распространения света в однородной среде и позволила рассмотреть дифракцию с количественной точки зрения.
Внимание! Закон прямолинейного распространения света и другие законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны.
Дифракционные картины от различных препятствий
Расчеты Френеля получили экспериментальное подтверждение. Из-за малой длины световой волны угол ее отклонения от прямолинейного направления распространения небольшой. Поэтому наблюдать дифракцию можно только при использовании очень маленьких препятствий. Другой вариант наблюдения этого явления — расположение экрана вдали от препятствия.
Так, чтобы наблюдать дифракцию при расстоянии между экраном и препятствием в 1 м, размеры этого препятствия должны составлять сотые доли миллиметра. Если расстояние от препятствия до экрана увеличить до нескольких сотен метров, то размеры препятствия могут быть несколько сантиметров. Если расстояние между экраном и препятствием будет составлять несколько километров, дифракцию можно будет наблюдать при размерах препятствия в несколько метров.
Дифракционная картина — картина на экране, полученная в результате интерференции вторичных световых волн.
Подобную картину вы уже видели на картинке, иллюстрирующей опыт Юнга. Так, дифракционная картина от двух малых щелей — это чередующиеся темные и светлые полосы. Если использовать другие препятствия, картина будет меняться. На рисунке ниже схематично показаны дифракционные картины от различных препятствий: а — от тонкой проволочки; б — от круглого отверстия; в — от круглого экрана.
Вместо тени проволочка оставляет на экране светлые и темные полосы. В центре дифракционной картины, полученного от отверстия, появляется темное пятно, окруженное светлыми и темными кольцами. В центре тени, образованной круглым экраном, видно светлое пятнышко, а сама тень окружена темными кольцами. Если изменять диаметр отверстия, в центре дифракционной картины можно получить как светлое, так и темное пятно, окруженное либо темными, либо светлыми кольцами соответственно.
Дифракционная решетка
Дифракционная решетка — оптический прибор, принцип действия которого основан на явлении дифракции.
Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками. Ее изготавливают путем нанесения на стекло штрихов. Их число может доходить до нескольких тысяч на 1 мм. Общее их число часто превышает 100 тысяч. Решетку также можно получить из металла, на котором чередуются участки, отражающие и рассеивающие свет.
Период дифракционной решетки равен сумме ширины прозрачных щелей и ширины непрозрачных промежутков:
Внимание! Обычно изготавливают дифракционные решетки с периодом в 10 мкм.
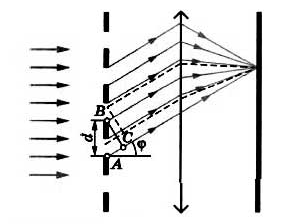
Пусть на дифракционную решетку с периодом d падает плоская монохроматическая волна, длина волны которой составляет λ.
При этом вторичные источники, расположенные в щелях решетки, создают световые волны, распространяющиеся по всем направлениям. Найдем условие, при котором идущие от щелей волны усиливают друг друга (складываются). Для этого рассмотрим волны, распространяющиеся в направлении под углом φ к дифракционной решетке.
Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке вмещается целое число длин волн, то волны от всех щелей при сложении будут усиливать друг друга. Из треугольника АВС найдем длину катета АС:
При этом максимумы будут наблюдаться под углом φ в соответствии с условием:
где величина k = 0, 1, 2, … определяет порядок спектра.
Нужно учитывать, что при выполнении условия друг друга усиливают как волны, распространяющиеся от нижних краев щелей, так и волны, распространяющиеся от всех других точек щелей. Каждой точке в первой щели соответствует точка во второй щели, находящаяся на расстоянии d от первой точки. Поэтому разность хода испущенных этими точками вторичных волн равна kλ, и эти волны взаимно усиливаются.
Рассмотрим следующий случай. За решеткой поместим собирающую линзу, а за ней — экран на фокусном расстоянии от линзы. Линза фокусирует лучи, идущие параллельно, в одной точке (в фокусе). В этой точке волны складываются и взаимно усиливаются. Углы φ, удовлетворяющие условию, определяют положение так главных максимумов на экране (соответствующих 1, 2 и т.д. порядку).
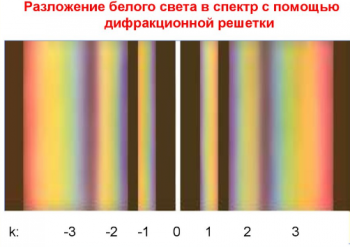
Наряду с картиной, получаемой в результате дифракции света, в случае дифракционной решетки наблюдается дифракционная картина и от отдельных щелей. Интенсивности максимумов в ней меньше интенсивности главных максимумов. Так как положение максимумов (кроме центрального, соответствующего k = 0) зависит от длины волны, то решетка разлагает белый свет в спектр. Чем больше λ, тем дальше от центрального максимума располагается тот или иной максимум, соответствующий данной длине волны.
Каждому значению k соответствует свой порядок спектра. Между максимумами расположены минимумы освещенности. Чем больше число щелей, тем более резко очерчены максимумы и тем более широкими минимумами они разделены.
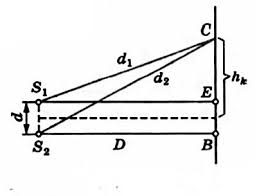
Пример №1. В опыте Юнга по дифракции расстояние между щелями равно d = 7∙10 –4 м. Расстояние от двойной щели до экрана равно D = 2 м. При освещении прибора зеленым светом расстояние между соседними светлыми дифракционными полосами оказалось равным ∆h = 16∙10 –2 м. Вычислите длину волны.
В некоторой точке С экрана будет наблюдаться максимум освещенности при выполнении условия:
где величина k = 0, 1, 2, … — целые числа.
Применим теорему Пифагора к треугольникам S1CE и SsCB:
Вычитая из первого равенства второе, получаем:
d 2 2 − d 2 1 = 2 h k d
( d 2 + d 1 ) ( d 2 − d 1 ) = 2 h k d
Так как расстояние между щелями много меньше расстояния между ними и экраном, то можем считать, что:
Отсюда можем найти расстояние k-той светлой полосы от центра экрана:
Расстояние между соседними полосами равно:
На плоскую непрозрачную пластину с узкими параллельными щелями падает по нормали плоская монохроматическая волна из красной части видимого спектра. За пластиной на параллельном ей экране наблюдается интерференционная картина, содержащая большое число полос. При переходе на монохроматический свет из синей части видимого спектра
а) расстояние между интерференционными полосами увеличится
б) расстояние между интерференционными полосами уменьшится
в) расстояние между интерференционными полосами не изменится
г) интерференционная картина станет невидимой для глаза
Алгоритм решения
Решение
Зависимость расстояния между интерференционными полосами от частоты световых лучей удалось установить экспериментально. Было выяснено, что чем выше частота, тем меньше расстояние между ними. Частота света из синего части спектра больше частоты из красной части спектра. Поэтому при переходе из красной части спектра в синюю часть расстояние между полосами интерференционной картины уменьшится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В прозрачном сосуде, заполненном водой, находится дифракционная решётка. Решётка освещается лучом света лазерной указки, падающим перпендикулярно её поверхности через боковую стенку сосуда. Как изменятся частота световой волны, длина волны, падающей на решётку, и угол между падающим лучом и первым дифракционным максимумом при удалении воды из сосуда?
Для каждой величины определите соответствующий характер изменения:
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Когда воды в сосуде не станет, изменится оптическая плотность среды — ею будет воздух, имеющий абсолютный показатель преломления 1 (у воды он равен 1,33).
Частота световой волны — величина постоянная. Она не меняется при изменении любых величин.
Длина световой волны меняется с учетом оптической плотности среды. Она определяется формулой:
В оптически более плотной среде скорость распространения волны уменьшается. Но когда их сосуда была удалена вода, оптическая плотность уменьшилась, значит, скорость волны увеличилась. Так как частота волны — постоянная, а длина волны прямо пропорциональна ее скорости, то при увеличении скорости длина волны тоже увеличится.
В оптически более плотной среде волны отклоняются от прямолинейного распространения сильнее в сторону нормали. Поэтому при удалении воды, когда оптическая среда станет менее плотной, лучи отклонятся от нормали. В этом случае угол между нормалью к решётке и первым дифракционным максимумом увеличится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Дифракционная решётка с периодом 10 –5 м расположена параллельно экрану на расстоянии 0,75 м от него. На решётку по нормали к ней падает пучок света с длиной волны 0,4 мкм. Какого порядка максимум в спектре будет наблюдаться на экране на расстоянии 3 см от центра дифракционной картины? Считать sina ≈ tga.