если уровень значимости 5 ный чему будет равен уровень вероятности

Доверительные вероятности и уровни значимости.

По выборочным характеристикам можно построить интервал, в котором с той или иной вероятностью находится генеральный параметр. Вероятности, признанные достаточными для уверенного суждения о генеральных параметрах на основании выборочных показателей, называют доверительными.

Понятие о доверительных вероятностях вытекает из принципа, что маловероятные события считаются практически невозможными, а события, вероятность которых близка к единице, принимают за почти достоверные. Обычно в качестве доверительных используют вероятности Р₁ = 0.95, Р₂ = 0.99, Р₃ = 0.999. Определенным значениям вероятностей соответствуют уровни значимости, под которыми понимают разность α = 1–Р. Вероятности 0.95 соответствует уровень значимости α₁= 0.05 (5%), вероятности 0.99 – α₂ = 0.01 (1%), вероятности 0.999 – α₃ = 0.001 (0.1%).

Это означает, что при оценке генеральных параметров по выборочным показателям существует риск ошибиться в первом случае 1 раз на 20 испытаний, т.е. в 5% случаев; во втором – 1 раз на 100 испытаний, т.е. в 1% случаев; в третьем – 1 раз на 1000 испытаний, т.е. в 0.1% случаев. Таким образом, уровень значимости обозначает вероятность получения случайного отклонения от установленных с определенной вероятностью результатов. Вероятности, принятые как доверительные, определяют доверительный интервал между ними. На них можно основывать оценку той или иной величины и те границы, в которых она может находиться при разных вероятностях.

Для различных вероятностей доверительные интервалы будут следующими:

— Р₁ = 0.95 интервал – 1.96σ до + 1.96σ (рис. 5)

— Р₂ = 0.99 интервал – 2.58σ до + 2.58σ

— Р₃ = 0.999 интервал – 3.03σ до + 3.03σ

Доверительным вероятностям соответствуют следующие величины нормированных отклонений:

— вероятности Р₁ = 0.95 соответствует t₁ = 1.96σ

— вероятности Р₂ = 0.99 соответствует t₂ = 2.58σ

— вероятности Р₃ = 0.999 соответствует t₃ = 3.03σ

Выбор того или иного порога доверительной вероятности осуществляют исходя из важности события. Уровень значимости в таком случае – эта та вероятность, которой решено пренебрегать в данной исследовании или явлении.

Средняя ошибка (m), или ошибка репрезентативности.

Выборочные характеристика, как правило, не совпадают по абсолютной величине с соответствующими генеральными параметрами. Величину отклонения выборочного показателя от его генерального параметра называют статистической ошибкой, или ошибкой репрезентативности. Статистические ошибки присущи только выборочным характеристикам, они возникают в процессе отбора вариант из генеральной совокупности.

Средняя ошибка вычисляется по формуле:

(5) ,

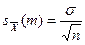
где σ – среднее квадратическое отклонение,

n – количество измерений (объем выборки).

Выражается в тех же единицах измерения, что и .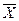

Величина средней ошибки обратно пропорциональна численности выборочной совокупности. Чем больше размеры выборки, тем меньше средняя ошибка, а следовательно, меньше расхождение между значениями признаков в выборочных и генеральной совокупностях.

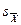
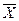
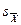
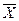
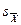
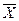
Среднюю ошибку выборки можно использовать для оценки генеральной средней согласно закону нормального распределения. Так, в пределах ±1 находится 68.3% всех выборочных средних арифметических , в пределах ±2 – 95.5% всех выборочных средних , в пределах ±3 – 99.7% всех выборочных средних .

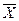
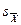
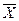
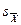
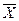
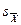
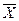
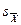
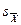
Поэтому, зная среднюю арифметическую выборки и среднюю ошибку выборки , можно с определенной степенью вероятности судить о пределах, в которых заключены возможные величины выборочных средних. Средняя арифметическая выборки с учетом средней ошибки записывают с виде ± , либо ±2 , либо ±3 в зависимости от значений лимитов (Х_max и Х_min). Лимиты при нормальной распределении не должны отклоняться за пределы 3 .

Источник

Б) ССВУ (SWOT-анализ)

40. Что означает: «часть объектов генеральной совокупности, включенных в обследование для характеристики совокупности по нужным признакам»?

б) выборка;*

в) определенное множество;

41. Какие этапы научного планирования выделяются при проведении исследований?

а) планирование, проведение эксперимента, формулирование выводов;

б) планирование, закладка эксперимента, накопление первичных данных, математический анализ с последующим формулированием выводов и предложений производству;*

в) проведение исследований, математическая обработка полученных данных;

г) планирование, накопление первичных данных, формулирование выводов и предложений производству.

42. Какие методы предназначены для накопления первичных данных об объектах исследования?

а) наблюдение и дисперсионный анализ;

б) эксперимент и вариационный анализ;

в) наблюдение и эксперимент;*

г) вариационный анализ и дисперсионный анализ.

43. Какой из методов научного исследования подразумевает «искусственное создание разных условий для исследуемых растений с целью определения наиболее эффективных в процессе учетов и наблюдений»?

в) эксперимент;*

44. Что называют вариантами опыта?

а) обработку почвы и удобрения;

б) определенная разновидность исследуемого фактора, от которого надеются получать лучшие результаты;*

в) повторения в опыте;

г) разновидности опытов.

45. Что такое схема эксперимента?

а) размещение вариантов и повторений на опытном участке;

б) перечень опытных и контрольных вариантов, включаемых в эксперимент для проверки гипотезы;*

в) чертеж, на котором размещены границы эксперимента;

г) перечень методов исследования, которые планируется проводить в эксперименте.

46. В каких опытах изучается влияние нескольких факторов?

б) многофакторных;*

47. Что означает: «научное предположение, истинное значение которого является неопределенным «?

г) гипотеза.*

48. Что означает: «целенаправленное сосредоточение внимания исследователя на явлениях эксперимента или природы, их количественная и качественная регистрация»?

б) наблюдение;*

в) статистический анализ;

49. Что означает «воспроизводимость результатов опыта»?

а) при повторе опыта в идентичных условиях и при аналогичных методиках должны получить аналогичные результаты;*

б) результаты опыта должны быть такими же и в других почвенно-климатических зонах;

в) в следующем году исследований результаты опыта должны повториться;

г) что даже при изменении условий опыта и методик исследования результаты опыта должны подтвердиться.

50. Если уровень значимости 5%-ный, чему будет равен уровень вероятности?

б) 95 %;*

51. Как расшифровывается НСР:

а) наибольший существенный результат;

б) head certain point;

в) наибольшая средняя разница;

г) наименьшая существенная разность.*

52. Какая разновидность ошибок приводит к завышению или занижению результатов исследований под действием определенных факторов (закономерных изменений плодородия почвы и др.)?

а) систематические;*

53. Как называются ошибки, возникающие при просчетах в процессе работы?

в) грубые;*

54. По какой формуле находится стандартное отклонение?

а) ;

б) ;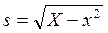

в) ;*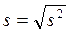

г) .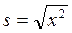

55. По какой формуле находят погрешность выборочной средней?

а) ;*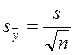

б) ;

в) ;

г) .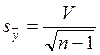

56. Какая проявляется форма корреляции, когда при увеличении одних признаков соответственно увеличиваются другие признаки?

б) прямолинейная;*

57. Когда исследуется связь между двумя признаками, то это корреляция?

а) простая;*

58. Степень и особенности изменения одного из признаков (Х) на единицу другого (Y) – это.

г) регрессия.*

59. Модель – это:

а) иерархическая система принципов системного анализа;

Источник

Уровни статистической значимости

Результаты математической обработки данных почти любым методом в конечном итоге оцениваются по уровню статистической значимости полученного результата. Это может быть уровень значимости коэффициента корреляции (Пирсона, Спирмена), уровень значимости различий по результатам сравнения выборок по тому или иному статистическому критерию (Стьюдента, Манна-Уитни, Вилкоксона, Хи-квадрат) и т.п. — вне зависимости от используемого метода, уровни значимости оцениваются одинаково.

Уровень статистической значимости обозначается латинской буквой p. Традиционно выделяют три уровня статистической значимости результатов математической обработки данных:

Кроме того, иногда в результатах исследований выделяют и описывают также близкие к статистически значимым результаты (p≈0,05). Сюда можно отнести такие показатели статистической значимости, как 0,06, 0,07, 0,08 и 0,09. Они свидетельствуют о наличии тенденции к существованию соответствующей закономерности.

Что касается показателей статистической значимости величиной от 0,1 и выше — они говорят о том, что полученный результат не является статистически значимым. Например, если речь идет о сравнении выборок, то подобный показатель свидетельствует об отсутствии статистически значимых различий между сравниваемыми выборками.

По сути уровень статистической значимости отражает вероятность ошибки в выявлении закономерности. Поэтому чем меньше величина показателя p, тем ниже вероятность ошибки, тем более статистически значимым является полученный результат.

Источник

Как выбрать уровень статистической значимости для AB-теста и как интерпретировать результат

Регистрация по номеру телефона

Вы работаете над повышением количества регистраций, внимательно рассматриваете этапы прихода новых пользователей, замечаете, что многие отваливаются на этапе ввода своего email и решаете попробовать заменить email на номер телефона. Пусть это не совсем общепринято и требует отправки небесплатной смски, но сегодняшние пользователи не очень любят электронную почту и часто регистрируются прямо с телефона.

Планирование эксперимента

Допустим, мы спланировали эксперимент с любым из обычных калькуляторов оценки требуемого количества пользователей, всё сделали аккуратно, выбрали одностороннюю гипотезу (нас интересуют только улучшения) и.. какой же уровень статистической значимости выбрать?

Что результаты значат на самом деле

Если телефонные регистрации ничуть не лучше, в некоторых тестах они всё равно будут случайно выигрывать.

P-value AB-теста как раз и показывает, насколько редкое событие мы наблюдаем, если бы предложение вводить номер телефона на самом деле (на длительном периоде времени) ничего не улучшало, а возможно даже и ухудшало.

Представьте себе, что в такой печальной ситуации мы провели бы не один, а сотню одинаковых AB-тестов: каждый по те же пять недель, каждый по 10000 посетителей на вариант. В большинстве таких ста тестов телефонный вариант принесёт меньше регистраций, чем email-вариант или столько же, как и email-вариант. Однако в части тестов телефонный вариант может принести немного больше регистраций.

Наблюдаемое p-value 0.07 как раз и означает, что если телефонный вариант на самом деле ничуть не лучше email’ового, то оказаться впереди email’ового столь сильно или ещё сильнее, чем мы наблюдаем, он смог бы в семи тестах из ста.

Выбор уровня статистической значимости показывает, насколько редкой должна быть наблюдаемая разница в конверсиях между телефонным и email’овым вариантами, чтобы мы всё же признали такую разницу слабо объяснимой случайной флуктуацией и решили переключиться на телефонные номера.

Стоимость ошибочного выигрыша

Ключевой момент интерпретации состоит в том, что даже если мы всё проводим аккуратно, без технических и логических ошибок, то наши AB-тесты всё равно время от времени обязательно будут «подтверждать» ложные гипотезы. Если мы будем принимать решения на основании тестов, то периодически будем ошибаться. Мы лишь можем ограничить количество ошибок, выбирая тот или иной уровень статистической значимости.

В общем-то пользу от теста и стоимость возможных ошибок при том или ином уровне значимости можно прикинуть с помощью очень простых расчётов. В примере ниже мы подсчитываем результат в новых пользователях, но не намного более сложным образом можно оценивать ожидаемые результаты и в деньгах.

Пользуясь нашими знаниями предметной области и историей предыдущих улучшений предположим, что удачный переход на телефонные регистрации повысит конверсию процентов на 5, а если мы ошибочно перейдём на телефонные регистрации, то возможно и половина посетителей не сможет или не захочет регистрироваться (откуда именно берём такие допущения расскажем ниже).

Среднее количество регистраций в неделю

Насколько больше пользователей может приносить телефонная регистрация по сравнению с емейловой

Насколько меньше пользователей может приносить телефонная-регистрация в случае ошибки

Если всё отлично, то год работы с смс-регистрацией принесёт дополнительно пользователей

Если ошибочно внедрили смс-регистрации, то за год недосчитаемся пользователей

52 * 2000 * 50% = 52000

Выбранный граничный уровень значимоcти

Если бы не проводили никаких улучшений, то за год появилось бы пользователей

Если бы проводили подобные эксперименты постоянно и принимали решения с таким же уровнем значимости, то за год средний эксперимент мог бы принести дополнительно пользователей

Пользы от среднего подобного эксперимента в процентах роста аудитории

Выбор уровня статистической значимости

Откуда же до начала эксперимента подставлять в такую таблицу ожидаемую пользу от справедливо выигравшего теста (5% в нашем примере) и возможный вред в случае ошибки (50% в нашем примере)? Лучше всего, конечно, опираться на историю подобных изменений. Если это далеко не первый эксперимент с улучшением воронки регистраций, и большинство из предыдущих увеличивало конверсию на пару процентов, то вряд ли даже очень значительная идея улучшит сильнее, чем на 5-10%.

Если истории подобных внедрений нет или она незначительна, то я не знаю метода лучше, чем экспертные оценки и страхи. Всё же вряд ли аж половина потенциальных пользователей не регистрируется, потому что не хотят / не могут вводить email, а телефон с радостью ввели бы. В лучшем случае миграция на номер телефона подтянет долю регистрирующихся с 7.7% может быть до 8% (улучшение на 5%). А вот если мы ошибаемся и пользователи на самом деле вообще не хотят доверять нам номер телефона, то можно/страшно потерять и половину регистраций.

Что же, если вся предыдущая команда сервиса была уволена вчера, мы очень мало знаем, о рынке и потенциальных пользователях, то действительно, наши идеи могут иметь мало смысла и неплохо бы проверять идеи улучшений построже.

Культура постоянных небольших экспериментов к сожалению может отвлекать от придумывания действительно прорывных идей, но может принести очень немаленькую пользу, оптимизируя существующие решения.

Можно наблюдать и после принятия решений

Было бы здорово даже в случае выигравшего эксперимента понаблюдать за пользователями более долговременно. Например, если по результатам наших пяти недель регистрация по номеру телефона выиграла, мы можем включить её для 95% анонимных посетителей. Оставшимся пяти процентам можно предлагать по прежнему email и сравнить результаты различных вариантов не через пять, а через 25 недель.

Проверяйте идеи, имеющие смысл

К счастью или к сожалению, но статистические исследования не избавляют от необходимости думать. Понимание рынка и его стандартов, пользователей и истории сервиса позволяет формулировать гипотезы, имеющие больший шанс улучшить ситуацию.

Некоторые изменения имеет смысл проводить, даже если мы не можем подтвердить положительный эффект

Как же подходить к выбору уровня значимости и анализу результатов?

Конечно же интерпретируйте результаты завершившихся тестов с помощью калькулятора, который правильно формулирует результаты. Например, с помощью productab.com, сделанным вашим покорным слугой

Прикиньте стоимость ошибок экспериментов разного рода именно для вашего сервиса и выберите несколько стандартных или не очень стандартных правил. Например, вида:

«Эксперименты с возможной потерей клиентов тестируем с уровнем значимости 95%»

«Просто обычные небольшие улучшения тестируем с уровнем значимости 90%»

«Мелочи, вроде текстов и цветов в местах не касающихся оплаты товара, тестируем c 80%-тной значимостью и если калькулятор рекомендует длину эксперимента больше недели, то пропускаем тестирование совсем»

Ну и конечно, набирайте больше опыта, узнавайте пользователей лучше, чтобы инвестировать в эксперименты, которые на самом деле могут что-то улучшить. Возможно в эксперименты, меняющие весь процесс использования сервиса радикально. Например, что если в нашем воображаемом сервисе вообще отказаться от регистрации и принимать оплату от любого незарегистрированного посетителя, у которого есть банковская карта?

Благодарности

А как вы интерпретируете результаты AB-теста?

Насколько масштабный у вас продукт, как вы проводите тесты и выбираете уровень статистической значимости? Автор будет очень благодарен за советы по более понятной интерпретации результатов теста.

Источник

Взаимосвязь понятий «уровень значимости», достоверность и ошибка первого рода

При работе со статистическим отчетом, научной статьей или диссертацией Вы постоянно сталкиваетесь таким термином, как уровень значимости или альфа (ошибка первого рода), чаще всего этот уровень задается относительно 5% или вероятности р=о,05. Решение о достоверности различий или «статистически значимых различиях» принимается относительно этого порогового значения. В данной статье мы предлагаем читателю разобраться в том, почему так важен этот уровень и что он значит в практическом смысле.

Определение (словарь Дж. М. Ласта):

ОШИБКА ТИПА I (ERROR TYPE I; син. alpha-error — ошибка альфа)

ошибочное отклонение нулевой гипотезы, т.е. утверждение о том, что различия существуют, тогда как их нет.

Немного о смысле уровня значимости и достовернности различий

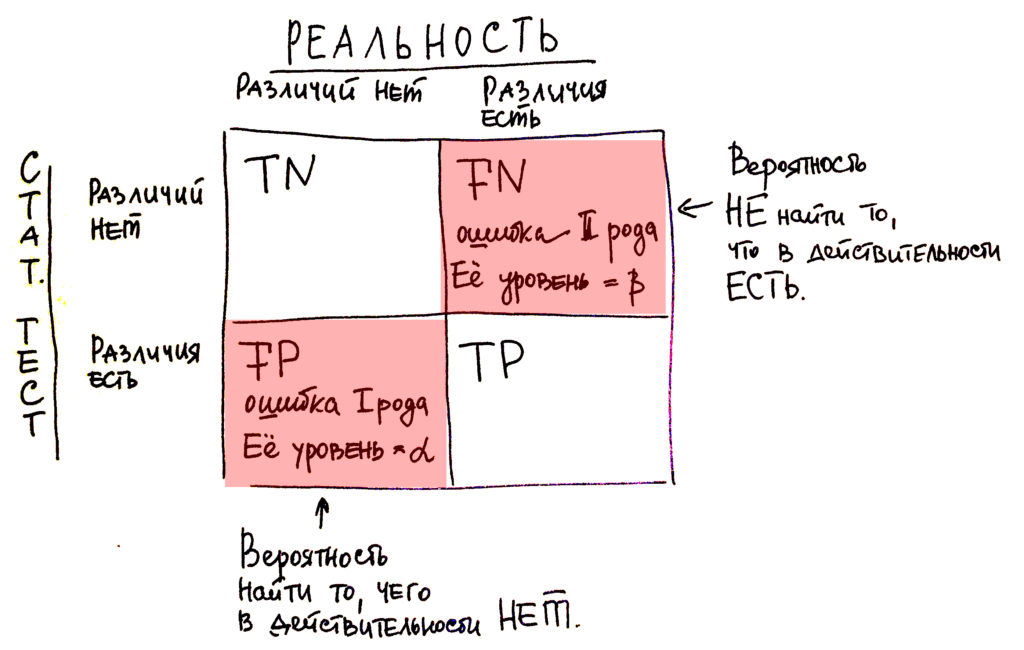
Для понимания темы статистических ошибок мы перейдем к простейшей матрице соотношения статистики (что она нам говорит по результатам статистических тестов) и реальности. Так вот, предположим, что статистика нам говорит о существовании связей, о существовании различий. В реальности же они также существуют, тогда мы считаем этот результат правильным положительным или truth positive (ТР). Например, статистика нам говорит об отсутствии связей, об отсутствии различий, а в реальности же они действительно существуют. Такая ситуация называется ложноотрицательной или false-negative (FN). Соответственно существуют ситуации, когда статистика нам говорит о существовании каких-то определенных взаимосвязей или о существовании различий, которые в реальности не существуют. Тогда это называется ложноположительной или false-positive (FP). И последний случай касается отсутствия по данным статистических тестов того, чего в действительности не существует, различий в действительности нет. И эта ситуация именуется как truth negative (TN) или ложноотрицательный результат.

Рисунок 1. Матрица соотношения реальность-результаты статистического теста. TN (true negative) — верноотрицательный, FN (false negative) — ложноотрицательный, FP (false positive) — ложноположительный, TP (true positive) — верно позитивный.

Так вот, как видно из этой матрицы, у нас существуют 2 ситуации, в которых мы можем ошибаться: это false-positive и truth negative. Это как раз два типа ошибок, о которых я говорил в начале этого блока: о ложноотрицательной ошибке и ложноположительной. Что на самом деле это значит?

Что в какой-то ситуации мы можем пересмотреть, а в какой-то – недосмотреть.

Пересмотреть, то есть найти то, чего в действительности нет, это является false-positive – это ошибка первого рода.

Или недосмотреть, то есть упустить то, что в действительности существует в реальности, но по данным статистических тестов мы чего-то не находим – это ложноотрицательный результат или ошибка второго рода.

Давайте нанесем те термины, которые, возможно, вы уже слышали – «уровень достоверности», «достоверные различия». Что это за слово такое «достоверность»? Оно относится как раз к ошибке первого рода и обозначается буквой α. Вы наверняка знаете обозначение уровня в р=0,05. Уровень достоверности в 0,05 как раз является критическим значением для результатов большинства статистических тестов ( 5 %). Мы делаем вывод относительно этих 5 %. Что в практическом смысле это значит? Что в 95 % мы находим различия, которые действительно существуют, и в 5 % даем себе возможность переобнаружить то, чего в действительности не существует в реальности.

Что касается ошибки второго рода, то здесь это уже не 5 %. И мы задаем либо 20, либо 10 %, что-то в этом диапазоне, это ошибка в 0,2; в 0,1. И как раз мы подходим к следующему чрезвычайно важному статистическому понятию как «мощность исследования». Мощность исследования это: (1 – β), где β это ошибка второго рода. Если стандартный уровень ошибки это 0,2 и 0,1, то мы получаем, что мощность исследования в норме составляет 0,8 или 0,9 (чаще, конечно, 0,8).

NB! по уровню значимости

Уровень значимости, то есть ошибки первого рода составляет чаще всего относительно уровня в 5 %, это уровень той ошибки, при которой мы даем возможность себе «перенайти» то, что в действительности не существует. В ошибке второго рода мы даем себе определенный люфт до 20 % не обнаружить того, что в действительности существует, то есть когда статистические тесты нам скажут, что чего-то нет, а в реальности эти различия существуют.

Источник