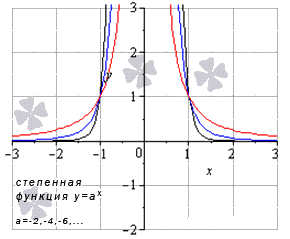
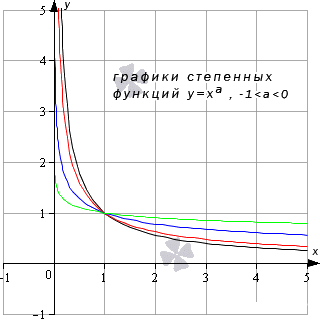
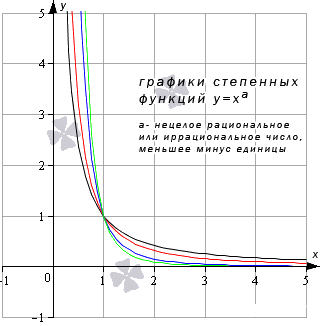
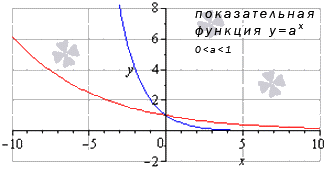
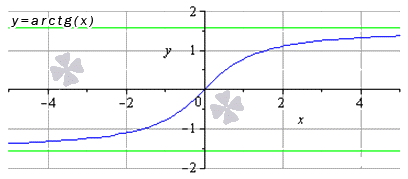
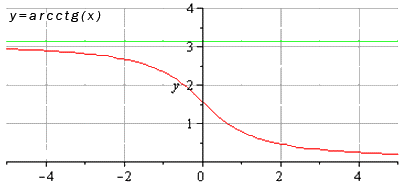
к чему стремится тангенс
Непосредственное вычисление пределов, таблица пределов функций
Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.
Значение предела в точке непрерывности определено значением функции в этой точке.
При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.
Произвести вычисление предела функции lim x → 5 a r c t g 3 5 · x
Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x 0 = 5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что
lim x → 5 a r c t g 3 5 · x = a r c t g 3 5 · 5 = a r c t g 3 = π 3
Для упрощения выражений применяют свойства пределов:
Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.
Таблица пределов функции
Для упрощения и решения пределов используется данная таблица основных пределов.
Функция корень n-ой степени
Для любых x 0 из опрелеления
lim x → x 0 x n = x 0 n
Функция корень n-ой степени
lim x → x 0 x n = x 0 n
Показательная функия
Для любых x 0 из области опреления lim x → x 0 a x = a x 0
Показательная функия
Для любых знвчений x 0 из област опредения lim x → x 0 a x = a x 0
Логарифмическая функция
Для любых x 0 из области опрелеления lim x → x 0 log a x = log a x 0
Логарифмическая функция
Для любых x 0 из области опрелеления
lim x → x 0 log a x = log a x 0
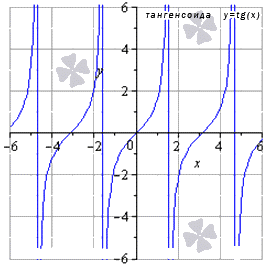
lim x → ∞ t g x не существует
Для любых x 0 из области опрелеления
lim x → x 0 t g x = t g x 0
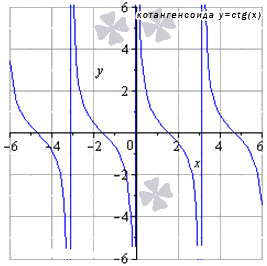
lim x → ∞ c t g x не существует
Для любых x 0 из области опрелеления
lim x → x 0 с t g x = с t g x 0
Обратные тригонометрические функции
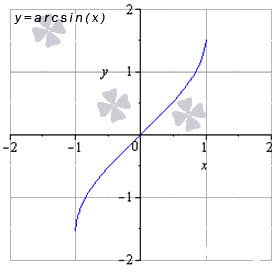
Для любых x 0 из области опрелеления
lim x → x 0 a r c sin x = a r c sin x 0
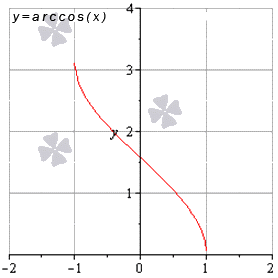
Для любых x 0 из области опрелеления
lim x → x 0 a r c c i s x = a r c cos x 0
Обратные тригонометрические функции
Для любых x 0 из области опрелеления
lim x → x 0 a r c t g x = a r c t g x 0
Для любых x 0 из области опрелеления
lim x → x 0 a r c c t g x = a r c c t g x 0
По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что
Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.
Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.
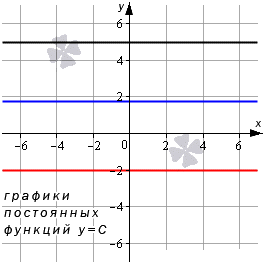
Предел константы
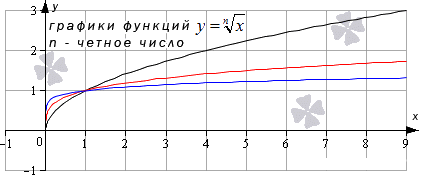
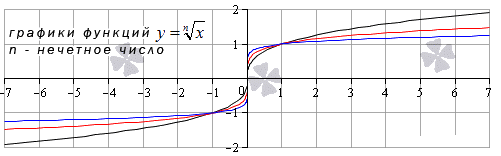
Предел функции корень n-ой степени
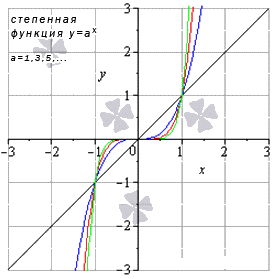
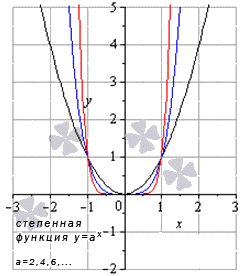
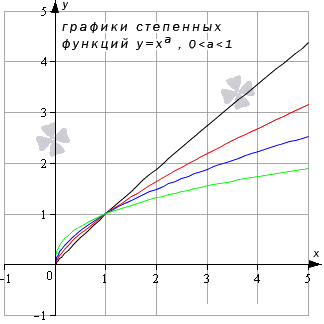
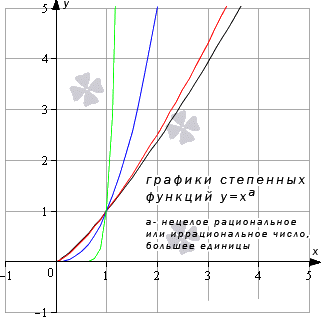
Предел степенной функции
Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.
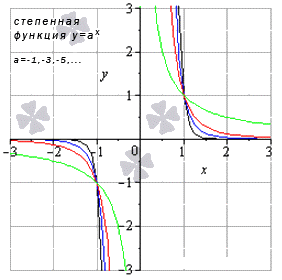
Предел показательной функции
Предел логарифмической функции
Предел тригонометрических функций
Предел обратных тригонометрических функций
Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.
Пределы с тригонометрическими функциями
Существует множество различных пределов тригонометрических функций. На помощь могут прийти основные методы вычисления:
Рассмотрим примеры подробного решения тригонометрических пределов для разбора каждого способа. Стоит отметить, что все методы можно комбинировать в одной задаче между собой для ускорения процесса вычисления.
Подставляем получившиеся преобразования, чтобы применить формулу первого замечательного предела.
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Обратим внимание на корень в числителе. От него нужно избавиться путём умножения и деления на сопряженное к нему число (отличающееся знаком между слагаемыми).
Видим, что в знаменателе появился синус, а это значит, что можно избавиться от него с помощью первого замечательного предела. Как в предыдущем примере одновременно умножаем и делим на аргумент синуса.
Подставляем преобразование синуса, чтобы применить замечательный предел.
Берем производные числителя и знаменателя дроби, стоящей в показателе экспоненты.
Подставляем полученное выражение под знак предела и пременяем свойство предела для показательной функции.
Итак, в пределе неопределенность ноль делить на ноль. Выполним замены на эквивалентные функции.
Подставляем в предел и получаем готовый ответ.
Первый замечательный предел
Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.
Формула
Для применения формулы необходимо, чтобы были соблюдены два условия:
Следствия
Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.
Примеры решений
Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей
В статье: «Первый замечательный предел, примеры решения» было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.
Примеры решения пределов тригонометрических функций с ответами
Простое объяснение принципов решения пределов тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения пределов тригонометрических функций
Для тригонометрических функций существует много разных пределов, но как правило, все они вычисляются, опираясь на первый замечательный предел и его следствия.
Первый замечательный предел выглядит следующим образом:
Главным следствием первого замечательного предела считают:
Также следствиями являются:
Нужна помощь в написании работы?
Примеры решения пределов тригонометрических функций
Задание
Найти предел функции:
Решение
Заменим значение х на число, к которому стремится функция:
Так как мы пришли на неопределённость вида 0/0, преобразуем синус так, чтобы он стал вида первого замечательного предела:
Мы знаем, что первый замечательный предел равен единице, следовательно
Таким образом найдём предел функции:
Задание
Найти предел функции:
Решение
При замене х на число, к которому он стремится, снова получаем неопределённость
Данную задачу можно решить, применив правило Лопиталя.
Найдём производные числителя и знаменателя функции и решим задачу:
Задание
Найти предел функции:
Решение
При подстановке нуля получим неопределённость типа 0/0:
Преобразуем функцию и упростим её:
Вынесем константу ½ за лимит и, пользуюсь свойством первого замечательного предела, найдём передел данной функции:
Задание
Найти предел функции:
Решение
Если заменить x на число, придём к неопределённости 0/0:
Для решения данного примера применим правило Лопиталя и заменим х на число в производных:
Задание
Вычислить предел функции:
Решение
Для решения данного примера воспользуемся свойством разности косинусов:
Вынесем минус за лимит, дабы не потерять и продолжим решение. Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:
Снова вынесем константы за лимит и получим вид первого замечательного предела, с помощью которого приходим к искомому решению:
Задание
Вычислить предел функции:
Решение
При подстановке х снова получаем неопределённость
Значит будем искать передел путём приведения к виду первого замечательного предела.
Представим тангенс в виде частного синуса х и косинуса х
Приведём к общему знаменателю и разделим выражение на множители следующим образом:
Мы видим первый замечательный предел, а значит, можем упростить до:
Далее снова приведём числитель к общему знаменателю:
Вновь разделим на множители и подставим значение х во второй косинус:
Таким образом нам остаётся разобраться с первым числителем. Поменяем местами 1 и косинус и вынесем минус за лимит.
Далее воспользуемся формулой понижения степени и найдём решение:
Задание
Вычислить предел функции:
Решение
При простом вычислении получаем неопределённость
Следовательно, будем вычислять предел, опираясь на правило первого замечательного предела. Приведём тангенс к виду частного синуса и косинуса:
Разделим пример на множители.
Приведём синусы к виду первого замечательного предела и получим ответ:
Задание
Найти предел функции:
Решение
При подставлении числа на место х приходим к неопределённости типа 0/0:
Преобразуем tg, приведем выражение к общему знаменателю cos x, вынесем общий множитель – sin x за скобку:
Используя следствие из первого замечательного предела, преобразим выражение и избавимся от тангенса.
Затем вновь приведем функцию к следствию первого замечательного предела и найдем ответ:
Задание
Найти предел функции:
Решение
При подстановке числа видим неопределённость.
Следовательно, искать предел будем, опираясь на правило первого замечательного предела. Для этого заменим переменную, которая будет стремиться к нулю:
Подставим в функцию:
Опираясь на свойства тригонометрии, заменим тангенс.
Зная, что предел косинуса нуля = 1, преобразуем пример и приведём к виду первого замечательного предела.
Найдём ответ.
Задание
Вычислить предел функции:
Решение
Здесь так же получим неопределённость:
Значит, введём новую переменную t:
Подставим получившиеся значения в пример и найдём предел:
Что такое предел функции
В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.
Определение предела функции
Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.
Запись предела:
Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):
Читается как “предел функции при икс, стремящемся к единице”.
x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).
Решение пределов
С заданным числом
Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):
Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).
С бесконечностью
В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:
Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:
Другой более сложный пример
Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.
Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.
С неопределенностью (икс стремится к бесконечности)
В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.
Пример: давайте вычислим предел ниже.
Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:
Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:
1. Находим x в старшей степени для числителя (в нашем случае – это два).
2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).
3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.
4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.
С неопределенностью (икс стремится к конкретному числу)
И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.
В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.
Пример: Найдем предел функции ниже.
1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.
2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
Знаменатель () изначально является простым.
3. Получаем вот такой видоизмененный предел:
4. Дробь можно сократить на ():
5. Остается только подставить число 1 в выражение, получившееся под пределом: