какова вероятность что монета упадет на ребро

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Теория вероятностей: ребро монетки

Последний раз редактировалось Лукомор 30.01.2017, 05:38, всего редактировалось 1 раз.

Последний раз редактировалось Shtorm 30.01.2017, 13:41, всего редактировалось 6 раз(а).

Вроде говорят, что 1 к 6000

Конечно, зависит от монеты.

Интересно увидеть их расчёт.

Это при изменении соотношения от до ?

Там, в книге, рисунок есть, поясняющий это действо.
Как я понял, если нормаль к горизонтальной поверхности пола через центр тяжести монеты проходит через ребро монеты, то монета встанет на ребро, а если через одну из сторон, то она упадет на сторону.

По поводу липкого пола ничего сказать не могу, на этом нигде не акцентируется внимание.

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Теория вероятностей: ребро монетки

И вот у меня вопрос к участникам форума: для равновероятного выпадения, нужно сделать чтобы площадь боковой поверхности была равна площади основания? Или чтобы площадь вертикального сечения цилиндра (в сечении прямоугольник) была равна площади основания цилиндра?
Итак вопрос: насколько верно я излагаю студентам это дело? И как бы Вы на моём месте поступили? Или как поступаете на моём месте?

Последний раз редактировалось Ether 30.01.2017, 01:32, всего редактировалось 1 раз.

Как мне кажется, для правильной двугранной монеты вероятность выпадения грани не будет зависеть от области изменения внешних условий при достаточной величине этой области.
Равновероятность выпадения граней толстой «трехгранной» монеты будет зависеть не только от её толщины, но и от внешних условий. Т.е. при изменении области внешних условий вероятность выпадения круглой грани и ребра для одной и той же «толстой» монеты может различаться, при том, что вероятность выпадения одной круглой грани будет равна вероятности выпадения другой круглой грани.

Заслуженный участник

Shtorm
Вот ещё один ответ можно добавить насчёт реальной монеты: пусть даже мы решили, как точно определить, что значит «встала на ребро» (а также «зависла в воздухе», «раздвоилась», «превратилась в горшок с петунией» и т. д.), а ещё лучше — точно определили себе, что значит, что она приземлилась на одну или вторую сторону, ведь это-то нам и надо. Тогда мы можем рассматривать только случаи, когда она приземлилась на одну из этих сторон, а когда встала на ребро — перекидывать. Тут вот как раз сегодня в другой теме поминали то, что условная вероятность — это обычная вероятность в «усечённом» вероятностном пространстве, и — не важно, какое у нас там было пространство, моделирующее капризную монету с выкрутасами — мы всегда сможем себе откусить от него пространство, моделирующее хорошую, приземляющуюся только двумя способами.

Про вероятность выпадения ребром в липком случае: даже если монета застревает накрепко и ничуть не наклоняется, всё ещё более-менее просто и зависит от того, считаем ли мы равномерно распределённой на сфере нормаль к монете или, скажем, угол между ней и горизонтом, и после этого ещё считать и считать. Почему вы решили, что достаточно сравнить площади?

Последний раз редактировалось Ether 30.01.2017, 01:43, всего редактировалось 5 раз(а).

Ну, для достаточно толстой монеты или цилиндра количество специсходов может быть достаточно существенным, и может быть хочется рассмотреть именно такую монету или цилиндр. С точки зрения теории и обоснования моделей это может быть интересным. Почему нет?

Заслуженный участник

Последний раз редактировалось Ether 30.01.2017, 01:51, всего редактировалось 1 раз.

Например необходимо построить физическую модель падения монеты, максимально приближенную к реальности. Для этого рассчитанные по физической модели вероятности должны будут соответствовать экспериментальным.
Задача непростая, но вполне может иметь место быть.

Последний раз редактировалось Shtorm 30.01.2017, 01:56, всего редактировалось 2 раз(а).

Хорошо. Забудем про монету. Подбрасываем цилиндрик. Как здесь быть?

Поддерживаю!

Заслуженный участник

Последний раз редактировалось Shtorm 30.01.2017, 02:02, всего редактировалось 2 раз(а).

Последний раз редактировалось Ether 30.01.2017, 02:21, всего редактировалось 3 раз(а).

Это идеальный симметричный случай, при котором существует равновероятность выпадения граней независимо от области в которой изменяются случайным образом внешние условия, при её достаточной величине. Можно рассматривать его как монету с ребром нулевой толщины.

При появлении асимметрии в геометрии монеты равновероятность выпадения граней будет уже зависеть не только от геометрии монеты, но и от области в которой изменяются внешние условия.

Заслуженный участник

Вроде говорят, что 1 к 6000

Конечно, зависит от монеты.

Заслуженный участник

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник

Как посчитать вероятность того, что подброшенная монетка упадёт на ребро и останется в состоянии покоя?

Вероятность, что первое касание поверхности будет = 33,33(3)%
Вероятность, что монета останется в таком положении = 50%.

Данные получены исходя из теории вероятности. Данные расчёты весьма поверхностны и применимы к абсолютным условиям (идеальным). Чтобы более точно подсчитать вероятности вам необходимо учесть все факторы, состав, свойства монеты и разумеется физические явления, воздействующие на монету, при условиях окружающей среды, в которой вычисляется данная вероятность.

предположи, что монета встаёт на ребро, когда в момент касания поверхности строго перпендикулярна ей (пренебрегая отскоком). в остальных случаях падает на бок. исходя из толщины монеты, оцени число возможных улов касания монетой поверхности из которых 1 соответствует успеху. я бы оценил такую вероятность как 1/(R*pi/d)=d/(pi*R), d-толщина монеты, R-диаметр монеты.

П. С. с отскоком все сложнее.

0. Кинетическая энергия будет настолько высокой, что монета обязательно отскочит. А по условию монету нельзя подбросить на полвысоты или несколько высот самой монеты (когда её кинетическая энергия позволит ей после падения остаться неподвижной). Она даже при падении с половины своей высоты не останется неподвижной. Она немного подскочит. Бросок (т. е. сам опыт с подкидыванием монеты) возможен только на высоты в десятки высот монеты. А падение с такой высоты означает, что кинетическая энергия отбросит ударившуюся о поверхность монету.

Ещё, монеты в современном мире, чаще делают с рёбрышками, которые получаются путём обжима металлического кругляшка, т. е. рёбра будут не плоские, а будто бы скруглённые. Площадки для устойчивого стояния на ребре монеты нет и в помине. И даже, если монета без рёбер, то, всё равно, нет возможности её мгновенно остановить. Она всё равно отскочит.

Во всех современных монетах толщина настолько маленькая, что даже монеты без рёбер нелегко установить, — они будут падать. Короче, даже прямых рук мало. Тута шансов нет даже при установке вручную, а уж при броске-то и, подавно, шансы равны нулю.

Итого:
мешают следующие вещи:
• сам бросок как таковой;
• кинетическая энергия, задающая отскок и опрокидывающая по новой неизвестной траектории монетку;
• толщина монетки, которая не позволит ей остаться в равновесном положении;
• круглость монетки, которая помешает ей не укатиться, под воздействием реакции опоры после столкновения;
• скруглённые рёбра, не дающие надёжной опоры.

Да и вообще, даже если подбросить наковальню, даже она подскочит. Потому что есть реакция опоры. С какой силой ударят по опоре, с той же силой она вернёт силу удара упавшему на неё предмету, а потому произойдёт отскок.

14:06 26.10.2016

Источник

Исследовательский проект по физике: бросок монетки

Стандартный пример, который приводится в начале изучения теории вероятностей, – это бросок двухсторонней монетки. Утверждается, что события «монета упала решкой вверх» и «монета упала орлом вверх» равновероятны из-за симметрии. Мне стало интересно, как получить такой результат, используя более строгие физические рассуждения. К тому же, исследуя динамику броска, можно ответить и на другие вопросы:

Любое исследование начинается с построения физической модели и этот случай – не исключение. Будем считать, что монета имеет форму цилиндра и состоит из однородного материала (важно, что толщиной монеты мы не пренебрегаем). В начальный момент времени монета находится на высоте h над неупругой поверхностью, имеет вертикально направленную скорость и произвольно вращается. Далее делаем существенное упрощение: монета падает на поверхность без отскока.

Для того чтобы определить, на какую сторону упадет монетка, я решил посмотреть, как от времени зависит вектор нормали, проведенной к плоскости верхней грани. Например, если в момент падения вектор направлен вверх, мы получаем событие «монета упала верхней гранью вверх». Далее я связал изменение направления нормали с вектором угловой скорости, а угловую скорость выразил через момент импульса. Из-за того, что монета имеет цилиндрическую форму, тензор инерции устроен так, что нормаль просто вращается вокруг вектора момента импульса с постоянной угловой скоростью.

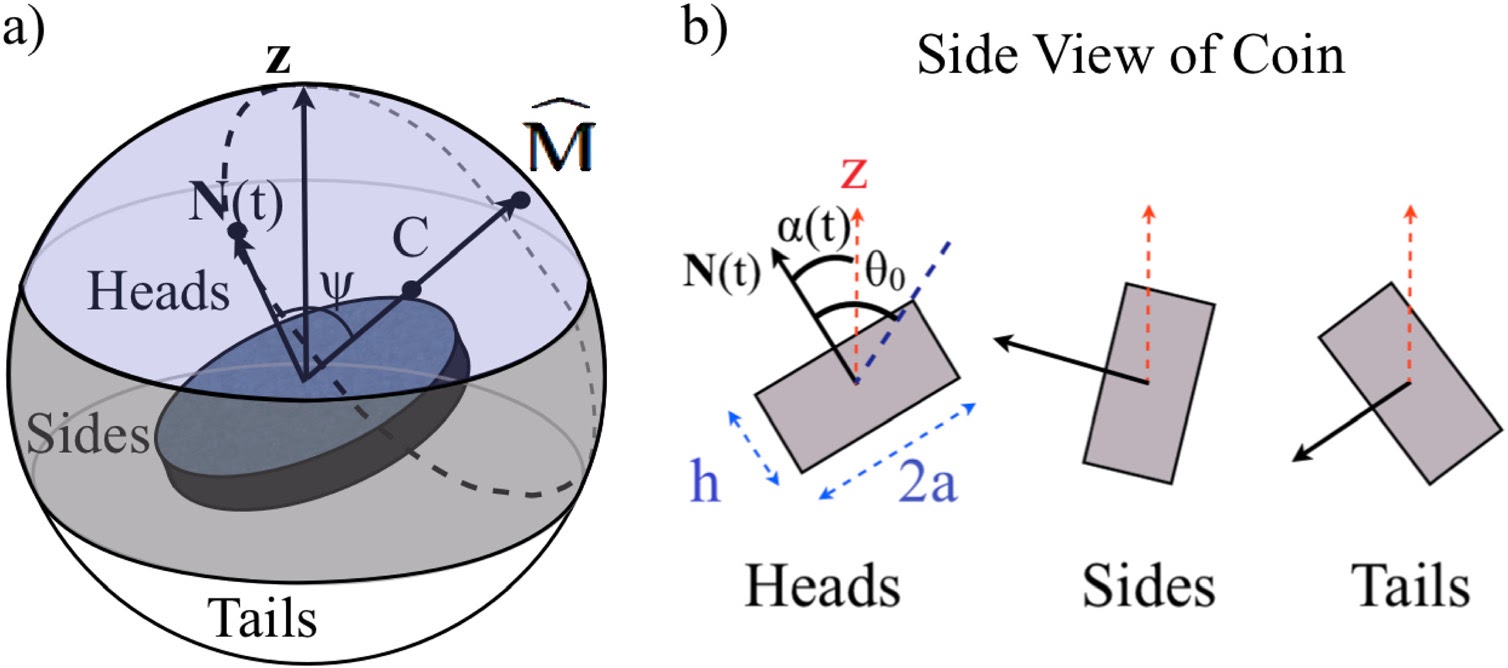
Пунктиром на рисунке (a) показано, как вектор нормали N вращается вокруг вектора момента импульса M. Заметим, что окружность, которую описывает вектор N, проходит через «северный полюс» сферы, потому что в начальный момент времени вектор N направлен вверх.

На рисунке (б) показано, как направление вектора N влияет на исход броска.

Уже с полученными явными математическими формулами для P(ζ, ψ) я принялся отвечать на поставленные вопросы. Взглянув на формулы, я пришел к достаточно неожиданным выводам: если ψ = π/2 (момент импульса лежит в плоскости монетки), то выпадение верхней и нижней стороны монетки равновероятно, но при ψ ≠ π/2 выпадение верхней стороны становится более вероятным. Это значит, что если во время броска немного подкрутить монету вокруг вертикальной оси, то на монете чаще будет выпадать та же сторона, что и была направлена вверх в начале броска. При этом вращение при таком броске визуально ничем не отличается от обычного броска. Именно в этом и заключается секрет фокуса.

Далее, исследуя зависимости вероятностей от толщины, я принял угол ψ равным π/2 и построил график этой зависимости:

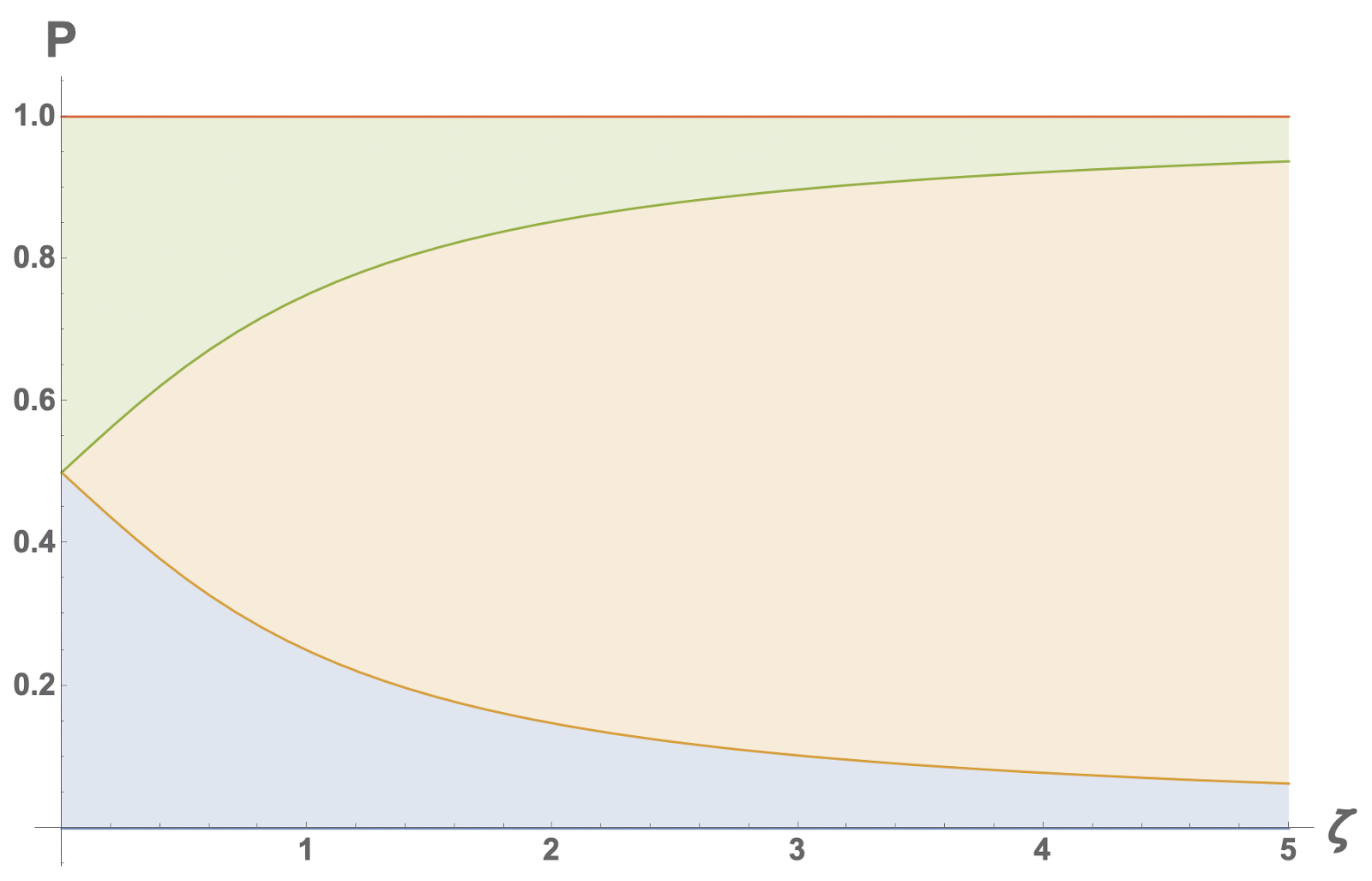
На графике синим цветом заливки обозначена вероятность события «падение решкой вверх», оранжевым – «падение на бок», и зелёным – «падение орлом вверх» (для фиксированного ζ толщина полоски определенного цвета равна вероятности).

В ходе подготовки доклада на реферативный семинар у меня получилось разобраться в физике броска, явно выразить вероятности через начальные условия и ответить на поставленные вопросы:

Я считаю, что посещение реферативных семинаров действительно полезно. На них мы не просто разбираем интересные физические сюжеты и осваиваем новые приёмы решения задач. Мы готовимся к научной работе: учимся искать материал по теме, вникать в статьи и обсуждать их с коллегами.

Источник

Толстая монета

Задача

Подбрасывая монетку, мы ожидаем, что выпадет или орел, или решка. Впрочем, иногда случается, что монетка падает и на ребро. Это, например, произошло, когда судья определял право розыгрыша мяча перед началом футбольного матча между сборными Колумбии и Парагвая на Кубке Америки 2016 года. Но там, очевидно, монетка застряла в траве.

В задачах по теории вероятности такие случаи не рассматривают, считая, что у математической монетки есть только две стороны, на которые она падает с равной вероятностью.

Давайте исправим эту несправедливость и дадим ребру монеты равные «права» с орлом и решкой: какой толщины должна быть монета, чтобы она выпадала и на стороны, и на ребро с одинаковой вероятностью 1/3?

Примечание. Для определенности считайте, что монета — это прямой круговой цилиндр с равномерно распределенной массой и что она падает на ровную поверхность без подскоков, как бы замирая на мгновение сразу после касания, после чего спокойно опускается на одну из двух сторон или на ребро в зависимости от своего положения при касании с поверхностью.

Подсказка

Рассмотрим монету в то мгновение, на которое она замирает, впервые коснувшись стола. Ребро мы тоже будем дальше называть стороной, то есть монетку считаем трехсторонней. В момент касания дальнейшая судьба монетки определяется только тем, как она расположена относительно вертикально направленной силы тяжести: она упадет на ту сторону, которую первой пересечет вектор силы тяжести (или его продолжение), идущий из центра масс монетки.

Поскольку подброс случайный, то и положение монетки в момент касания случайно. Значит, если взглянуть на эту ситуацию с точки зрения монетки (то есть считать, что она не двигается, а это весь мир вертится вокруг нее), то в момент касания направление вектора силы тяжести может быть любым и все направления равновероятны. То есть на сфере, которую образуют все возможные положения этого вектора, возникают три области, соответствующие сторонам монетки. А вероятности выпадения пропорциональны площадям этих областей. Осталось только понять, как они устроены, и посчитать площади.

Решение

Будем считать, что сфера из подсказки описана вокруг монетки (которую мы считаем цилиндром), — это чуть-чуть упростит дальнейшие рассуждения (такое допущение ни на что не влияет, потому что мы рассматриваем подобные сферы и все рассуждения про соотношения площадей и размеров от этого не страдают). Тогда на сфере возникают три области: две «шапки», соответствующие сторонам монетки, и полоса между ними, соответствующая ребру (рис. 1, слева). Чтобы у ребра была такая же вероятность выпадения, как у двух других сторон, нужно, чтобы площади всех трех областей были равны.

Рис. 1. Вид на монетку и описанную вокруг нее сферу сбоку. Если вектор силы тяжести попадает в верхнюю или нижнюю шапки, то монетка упадет на сторону. Если этот вектор попадает в пояс посередине, то монетка встанет на ребро

То есть задача свелась к вычислению площади сферической полосы, «зажатой» между двух плоскостей. Ее можно считать по-разному, но мы сейчас используем замечательное свойство сферы: оказывается, площадь такой полосы зависит только от расстояния между плоскостями (то есть не зависит от их положения относительно сферы). Из этого сразу следует, что толщина монетки должна быть равной трети диаметра сферы.

Послесловие

Возможно, у вас при решении получался ответ, в котором толщина монетки была в корень из 3 раз меньше ее диаметра. Скорее всего, вы считали вероятности, исходя из длин дуг окружности, описанной вокруг прямоугольника (сечения монетки плоскостью, проходящей через ее центр перпендикулярно боковой стороне монетки). Если так, то вы совершенно правильно посчитали.

Рис. 2. «Плоская» модель вращения монетки

Ваш ответ отличается от полученного выше, но это не значит, что он неправильный. Дело здесь не в подсчете, а в выборе модели того, как ведет себя монетка при броске. В решении было принято, что она может вращаться как угодно, и поэтому при приземлении может располагаться любым способом относительно поверхности. А вот если рассматривать вращение монетки только в одной плоскости, то и получается, что возможные направления вектора силы тяжести составляют окружность, а условие на равенство вероятностей означает, что ребро монетки должно быть видно из ее центра под углом 60°.

Разные модели приводят к разным вероятностным пространствам — это нормально. Мне кажется, что в данном случае поведение монетки лучше описывается именно моделью из решения. Некоторым подкреплением здесь служит байка о том, что Джон фон Нейман, которому задали вопрос этой задачи, когда он садился в такси, сообщил таксисту свой адрес и сразу же ответил. Причем, ровно так, как в решении. Правда это или нет — не знаю, но эта байка сопровождает задачу о «толстой» монете уже давно. Например, она приводится в прекрасной книжке Ф. Мостеллера «Пятьдесят занимательных вероятностных задач с решениями».

Что касается трюка в решении, благодаря которому не пришлось площадь поверхности сферического слоя, то этот факт — площадь слоя поверхности сферы между двумя параллельными плоскостями зависит только от расстояния между плоскостями (и не зависит от их положения относительно сферы) — можно установить разными способами. Например, можно «в лоб» найти эту площадь — найдя соответствующий интеграл. Или можно провести более «геометрическое» рассуждение (см. Spherical Surfaces and Hat Boxes). Кстати, оказывается, что площадь такого сферического слоя равна площади слоя, который эти же плоскости высекают на поверхности цилиндра, описанного вокруг данной сферы. Видимо, поэтому этот факт в англоязычной литературе называют «Теоремой о шляпных коробках» (Hat-Box Theorem).

Этот трюк, например, позволяет относительно просто решить следующую непростую задачку. Привожу ее формулировку ниже, а решение примерно через неделю появится в комментариях к этой задаче.

На плоскости нарисован круг радиуса 1. Имеется набор полосок бумаги бесконечной длины с параллельными краями. Полоски могут быть разной толщины, известно лишь, что их суммарная толщина меньше 1. Существует ли набор полосок с такими свойствами, которым можно покрыть полностью данный круг?

Источник