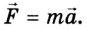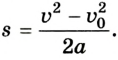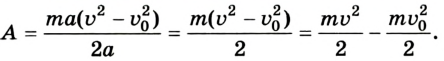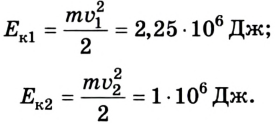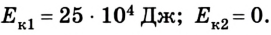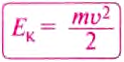кинетическая энергия измеряется в тех же единицах что и

Содержание:

Кинетическая энергия:

Иногда значение работы можно найти, не используя понятия силы и перемещения, на основании характеристики изменения энергии тела.

Рассмотрим тело массой m, на которое действует сила F. Направление действия силы совпадает с направлением перемещения. Работа, которую выполняет эта сила,

A = Fs.
Согласно второму закону механики Ньютона значение силы

Как известно, модуль перемещения равен:

Поэтому

Как известно, выражение 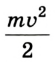называется кинетической энергией. Следовательно, для расчета работы достаточно определить только массу тела и его начальную и конечную скорости, т. е. знать изменение кинетической энергии тела. Такой метод удобен, поскольку им можно пользоваться даже в случае переменной силы и произвольной траектории.

Физическая величина, описывающая состояние движущегося тела и изменение которой определяет работу, называется кинетической энергией.

Для измерения энергии, как и работы, используется единица джоуль (Дж), названная в честь английского ученого Д. Джоуля.

Кинетической энергией обладает тело, движущееся в данной системе отсчета с определенной скоростью: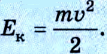
Скорость тела, измеренная в разных системах отсчета, будет иметь разное значение, т. е. она является относительной величиной. Поэтому кинетическая энергия тела постоянной массы тоже величина относительная и в разных системах отсчета имеет разное значение.

Рассмотрим, например, два железнодорожных вагона, массы которых составляют по 2 • 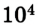кг, движущиеся в одном направлении со скоростями 15 м/с и 10 м/с относительно железнодорожного полотна, причем первый догоняет второго. Их кинетическая энергия соответственно будет:

Следовательно, при расчетах в разных инерциальных системах отсчета следует учитывать, что кинетическая энергия в случае перехода из одной системы в другую будет изменяться.

Что такое кинетическая энергия

Кинетической энергией обладает ветер, её используют для сообщения движения ветряным двигателям. Движущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их вращаться. На рисунке 175, а изображена ветряная мельница, в которой за счёт энергии ветра мелют зерно. Современные довольно мощные ветряные двигатели (рис. 175, б) используют для того, чтобы вырабатывать электроэнергию, качать из скважин воду и подавать её в водонапорные башни.

Движущаяся вода или нагретый пар, вращая турбины электростанции, теряет часть своей кинетической энергии и выполняет работу. Самолёт, летящий высоко в небе, кроме потенциальной обладает и кинетическуй энергией. Если тело находится в состоянии покоя, т. е. его скорость относительно Земли равна нулю, то и его кинетическая энергия относительно Земли будет равна нулю.

Опытами установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия. Выявленная зависимость математически выражается такой формулой:

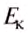
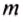
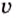
где — кинетическая энергия тела; — масса тела; — скорость движения тела.

Определение кинетической энергии

Наблюдения явлений природы показывают, что работа может выполняться при движении тел. Так, движущийся тепловоз, стыкуясь с вагоном, перемещает его на некоторое расстояние. Выполняется работа и в том случае, когда брошенный камень разбивает лед. Выстреленная из ружья пуля пробивает доску и т. п. Если потенциальной энергией обладают тела, на которые действует сила, то в упомянутых выше случаях работа выполняется потому, что они осуществляли перемещение, двигались.

Какой энергией обладают движущиеся тела

Энергию движущегося тела называют кинетической энергией.

Кинетическая энергия является физической величиной ее значение можно рассчитывать. Для этого необходимо знать, от каких физических величин она зависит.

Как рассчитывают кинетическую энергию

Поставим желоб под некоторым углом к поверхности стола. На некотором расстоянии от его нижнего конца поставим брусок. На средней части желоба разместим маленький стальной шарик и отпустим его. Скатившись по желобу, шарик ударится о брусок и переместит его на некоторое расстояние. Отметим расстояние, на которое сместился брусок.

Поместим шарик в верхней части желоба и отпустим его. В этом случае, скатившись желобом к основе, шарик приобрел большую скорость, чем раньше. Ударившись в брусок, он переместит его на большее расстояние, чем в предыдущем опыте, соответственно выполнив большую работу.

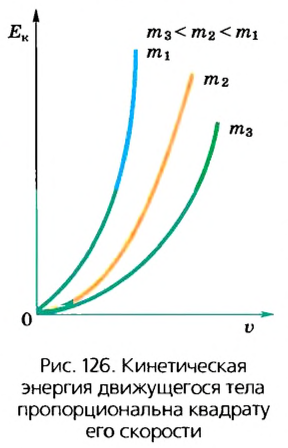
Таким образом, кинетическая энергия тела зависит от его скорости. Эта зависимость нелинейная, что заметно на графике зависимости кинетической энергии тела от его скорости. График имеет вид кривой линии (рис. 126).

Кинетическая энергия тела относительна

Последствия столкновения автомобилей в случае их движения навстречу друг другу будут всегда более ощутимы, чем тогда, когда один автомобиль догоняет другой.

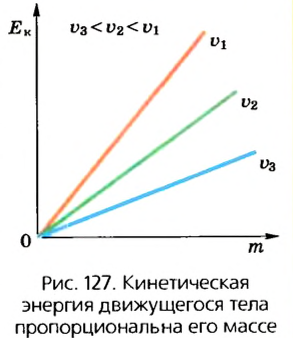
Кинетическая энергия зависит и от массы тела. Если повторим предыдущие опыты с шариком большей массы, то увидим, что перемещения бруска в этом случае будет большим. Эта зависимость линейная, поэтому можно сказать, что кинетическая энергия тела пропорциональна его массе (рис. 127).

Как рассчитать кинетическую энергию

Чтобы рассчитать кинетическую энергию, используют формулу:

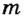
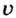
где — масса тела; — скорость тела.

Кинетическая энергия разных физических тел используется для выполнения механической работы. Так, опытные водители автомобилей время от времени отсоединяют двигатель от колес, выключая сцепление, и этим экономят топливо. Работа по преодолению сил трения выполняется за счет кинетической энергии автомобиля. Конструкторы работают над моделью городского автобуса, который начинает движение за счет энергии раскрученного во время стоянки большого маховика. Это дает возможность существенно уменьшить выбросы вредных газов в атмосферу и экономить топливо.

В южных областях Украины, в частности на Крымском полуострове, используют ветряные электростанции, которые работают за счет кинетической энергии потоков воздуха — ветра (рис. 128).

Кинетическая энергия тела

Рассмотрим движение тела массой т под действием нескольких сил, например движение санок (см. рис. 124). Предположим также, что сила натяжения веревок постоянна, а следовательно, постоянной будет и результирующая сила 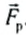. Она совпадает по направлению с перемещением тела или противоположна ему. Эта сила, естественно, вызывает ускорение санок, т. е. изменяет их скорость. Кроме того, она совершает работу. Следовательно, между работой результирующей силы и изменением скорости санок должна существовать связь.

Рассмотрим случай, когда проекция результирующей силы на направление движения положительна, т. е. санки движутся равноускоренно с ускорением а, которое находится из второго закона Ньютона:
(1)

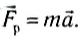
Работа результирующей силы:
A = F_p△r, (2)
где △r— модуль перемещения тела за некоторый промежуток времени. Подставим выражение (1) в (2). В результате получим:
A = ma△r. (3)

При равноускоренном одномерном движении модуль перемещения △r и изменение скорости связаны соотношением:
(4)
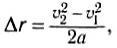
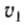
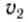
где и — начальная и конечная скорости тела, которое совершило перемещение △r с ускорением а.

Соотношение (3) с учетом (4) примет вид:
(5)

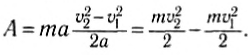
Полученная формула связывает работу результирующей силы, действующей на тело, с изменением величины 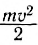. Эта величина называется кинетической энергией тела и обычно обозначается К.
Кинетическая энергия тела — это энергия движения. Она равна половине произведения массы тела на квадрат его скорости:
(6)

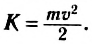
Тогда формула (5) примет вид:
(7)

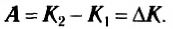
Итак, работа результирующей силы, действующей на тело, равна изменению кинетической энергии тела. Как вы уже знаете, изменение какой-то величины равно разности конечного значения и начального. Из формулы (7) очевидно следует, что кинетическая энергия выражается в тех же единицах, что и работа, т. е. в СИ в джоулях.

Когда результирующая сила действует по направлению движения тела и, следовательно, совершает положительную работу, то K₂>K₁. Это означает, что кинетическая энергия тела увеличивается. Понятно, что, если результирующая сила направлена в сторону, противоположную движению, она совершает отрицательную работу, и кинетическая энергия тела уменьшается. Следует отметить, что, хотя мы получили формулу (7) для частного случая равноускоренного и прямолинейного движения, она справедлива и в случае изменяющейся во времени результирующей силы. Поэтому формулу (7) часто называют теоремой о кинетической энергии.

Итак, любое движущееся тело (рис. 127, 128) обладает кинетической энергией. Поскольку скорость тела зависит от выбора инерциальной системы отсчета, то и кинетическая энергия также зависит от выбора системы отсчета. Очевидно, что, как и работа, кинетическая энергия является скалярной физической величиной. Она не зависит от направления движения тела, а определяется его массой и квадратом скорости.

Главные выводы:

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Кинетическая энергия – формула, единица измерения, определение и примеры кратко

Если система может совершить работу, то говорят, что она обладает энергией. Энергия — важная характеристика системы. Она не может исчезать и появляться, но имеет несколько видов и может переходить из одного вида в другой. Одним из таких видов является кинетическая энергия. В статье дадим определение этого понятия, выведем формулу кинетической энергии.

Формула кинетической энергии

Совершение работы в механике означает, что некоторая сила действует на материальную точку и перемещает ее. Согласно второму закону Ньютона материальная точка при этом получает некоторое ускорение, и ее скорость меняется.

Рис. 1. Второй закон Ньютона.

Из этой формулы видно, что работа, произведенная силой, равна разности двух величин, формулы которых различаются только скоростью. То есть эти величины характеризуют способность материальной точки совершать работу при изменении скорости, а значит, являются выражением энергии.

Кинетическая энергия тела имеет те же единицы измерения, что и работа, — Джоуль (Дж).

Рис. 2. Кинетическая энергия.

Свойства кинетической энергии

Если выписать в таблицу значения кинетической энергии движущейся материальной точки в разные моменты и работу, совершенную силой при этом, можно доказать теорему об изменении кинетической энергии.

Изменение кинетической энергии материальной точки за некоторое время равно работе, совершенной за это время силой, действующей на точку.

Таким образом, если работа силы положительна, то кинетическая энергия тела увеличивается, а если отрицательна — то уменьшается. Энергия, которой обладает движущаяся материальная точка, равна работе, которую надо совершить, чтобы разогнать ее от нуля до имеющейся скорости.

Важным свойством кинетической энергии является ее относительность. Действительно, скорость — величина, зависящая от системы отсчета. Следовательно, можно сделать вывод, что и кинетическая энергия в разных системах отсчета будет различной. К примеру, для внешнего наблюдателя движущийся автомобиль имеет большую кинетическую энергию, а для пассажира этого автомобиля его энергия равна нулю.

Если в системе имеется несколько независимых движущихся тел, то полная кинетическая энергия системы равна сумме кинетических энергий составляющих.

Рис. 3. Кинетическая энергия системы тел.

Еще одним свойством кинетической энергии является независимость от ее причины и источника. Движущееся тело будет обладать равной кинетической энергией независимо от того, что послужило причиной движения — то ли гравитационные силы, то ли силы упругости пружины, то ли внутренняя энергия топлива. Кинетическая энергия тела всегда будет зависеть только от его массы и скорости.

Что мы узнали?

Кинетическая энергия материальной точки — это величина, равная половине произведения массы точки на квадрат ее скорости. Изменение кинетической энергии материальной точки за некоторое время равно работе, совершенной за это время силой, действующей на точку.

Источник

Формула кинетической энергии

Определение и формула кинетической энергии

Кинетическую энергию тела определяют при помощи работы, которая совершается телом при его торможении от начальной скорости, до скорости, равной нулю.

Кинетическая энергия тела – мера механического движения тела. Она зависит от относительной скорости тел.

Встречаются следующие обозначения кинетической энергии: E_k,W_k,T.

Работу, которую производят над телом (A’) можно связать с изменением его кинетической энергии:

Кинетическая энергия материальной точки и тела

Кинетическая энергия материальной точки равна:

где m – масса материальной точки, p – импульс материальной точки, v – скорость ее движения. Кинетическая энергия является скалярной физической величиной.

Если тело нельзя принять за материальную точку, то его кинетическая энергия рассчитывается как сумма кинетических энергий всех материальных точек, которые составляют исследуемое тело:

В том случае, если тело (отличное от материальной точки) движется поступательно, то его кинетическую энергию можно рассчитать, применяя формулу (2), в которой все параметры отнесены к телу в целом.

При вращении тело вокруг неподвижной оси его кинетическую энергию можно вычислить, применяя формулу:

Если твердое тело совершает вращение относительно неподвижной точки (например, точки O), то его кинетическую энергию находят как:

Единицы измерения кинетической энергии

Основной единицей измерения кинетической энергии (как и любого другого вида энергии) в системе СИ служит:

в системе СГС –[E_k]= эрг.

При этом: 1 дж= 10 7 эрг.

Теорема Кенига

Для самого общего случая при расчете кинетической энергии применяют теорему Кенига. В соответствии с которой, кинетическая энергия совокупности материальных точек есть сумма кинетической энергии поступательного перемещения системы со скоростью центра масс (v_c) и кинетической энергии (E’_k) системы при ее относительном движении к поступательному перемещению системы отсчета. При этом начало системы отсчета связывают с центром масс системы. Математически данную теорему можно записать как:

Так, если рассматривать твердое тело, то его кинетическую энергию можно представить как:

Примеры решения задач

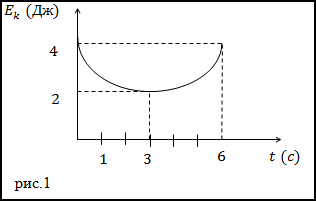
Задание. Какова работа, которая производится над телом за t=3 c (с начала отсчета времени), при силовом взаимодействии, если изменение кинетической энергии исследуемого тела задано графиком (рис.1)?

Решение. По определению изменение кинетической энергии равно работе (A’), которая производится над телом при силовом взаимодействии, то есть можно записать, что:

Исследуя график, приведенный на рис.1 мы видим, что за время t=3 c кинетическая энергия тела изменяется от 4 Дж до 2 Дж, следовательно:

Ответ. A’=-2 Дж.

Формула кинетической энергии не по зубам? Тебе ответит эксперт через 10 минут!

Решение. В качестве основы для решения задачи используем формулу, определяющую кинетическую энергию материальной точки:

Но по условию задачи:

Следовательно, можно приравнять правые части выражений (2.1) и (2.2), и получить:

Из второго закона Ньютона нам известно, что сила, действующая на частицу, будет равна:

При этом нормальное ускорение частицы (a_n), перемещающейся по окружности найдем как:

Тангенциальную составляющую ускорения (a_т)используя определение тангенциального ускорения, определение скорости ($v=\frac$) и выражение v(s) (2.3) вычислим как:

Используем выражения: (2.5), (2.6), (2.7), окончательно получаем для модуля силы:

Источник

Кинетическая энергия

Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек. Часто выделяют кинетическую энергию поступательного и вращательного движения.

Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением.

Содержание

История

Впервые понятие кинетической энергии было введено в трудах Г. Лейбница, посвященных понятию «живой силы»

Физический смысл

Рассмотрим систему, состоящую из одной частицы, и запишем второй закон Ньютона:

— есть результирующая всех сил, действующих на тело. Скалярно умножим уравнение на перемещение частицы . Учитывая, что , Получим:

Если система замкнута, то есть , то , а величина

остаётся постоянной. Эта величина называется кинетической энергией частицы. Если система изолирована, то кинетическая энергия является интегралом движения.

Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения:

— масса тела

— скорость центра масс тела

— момент инерции тела

— угловая скорость тела.

Физический смысл работы

Работа всех сил, действующих на частицу, идёт на приращение кинетической энергии частицы:

Релятивизм

При скоростях, близких к скорости света, кинетическая энергия любого объекта равна

— масса объекта;

— скорость движения объекта в инерциальной системе отсчета;

— скорость света в вакууме ( — энергия покоя).

Данную формулу можно переписать в следующем виде:

При малых скоростях () последнее соотношение переходит в обычную формулу .

Соотношение кинетической и внутренней энергии

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров), то тело неподвижно как единое целое, и можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — Постоянная Больцмана.

См. также

Полезное

Смотреть что такое «Кинетическая энергия» в других словарях:

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, энергия, которой обладает движущийся предмет. Получает ее, начав двигаться. Зависит от массы ( ) предмета и его скорости (v), согласно равенству: К. э. = 1/2mv2. При ударе преобразуется в другую форму энергии, такую как… … Научно-технический энциклопедический словарь

Кинетическая энергия — КИНЕТИЧЕСКАЯ ЭНЕРГИЯ, механическая энергия системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2 от mv2. В сумме с… … Иллюстрированный энциклопедический словарь

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механич. системы, зависящая от скоростей её точек. К. э. Т матер. точки равна: T=mv2/2, где m масса этой точки, v её скорость. К. э. механич. системы равна сумме К. э. всех её точек: T=Smkv2k/2. Выражение К. э. системы можно ещё… … Физическая энциклопедия

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — энергия механической системы, зависящая от скоростей движения составляющих ее частей. В классической механике кинетическая энергия материальной точки массы m, движущейся со скоростью v, равна 1/2mv2 … Большой Энциклопедический словарь

кинетическая энергия — ▲ энергия ↑ скорость, масса (материи) < > потенциальная энергия кинетическая энергия энергия, определяемая скоростью тела и его массой. механическая энергия. маховик … Идеографический словарь русского языка

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (энергия движения) запас энергии движущегося тела, превращающийся в другой вид энергии при прекращении движения. Напр. К. Э. пули, попадающей в мишень, превращается в теплоту. При поступательном движении тела его К. Э. равна половине произведения … Морской словарь

кинетическая энергия — Энергия, которой обладает движущееся тело; определяется как половина произведения массы на квадрат скорости. Для жидкости обычно говорят о плотности кинетической энергии мере количества энергии движения, которой обладает единица объема жидкости.… … Справочник технического переводчика

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — (см.) механического движения тела или системы тел, зависящая от скоростей их точек. К. э. поступательно движущегося тела равна половине произведения массы тела на квадрат его скорости: К э. системы тел равна сумме К. э. всех тел системы … Большая политехническая энциклопедия

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ — сила в движении, действующая сила движения; в отличие от потенциальной энергии силы в покое. Полный словарь иностранных слов, вошедших в употребление в русском языке. Попов М., 1907 … Словарь иностранных слов русского языка

Источник