книга дьяченко чего на свете не бывает

Чего на свете не бывает? Занимательные игры для детей от 3 до 6 лет

Оглавление

Игры для детей 3 лет

Игры для детей 4–5 лет

Игры для детей 6 лет

Предисловие

«Поиграй со мной!» – как часто слышим мы эту просьбу от своих детей. И сколько радости они получают, когда мы, преодолевая усталость и отодвигая домашние дела, соглашаемся хоть на несколько минут побыть больным или пассажиром, учеником или серым волком. Скажем прямо, чаще всего, играя с ребенком, мы следуем за его желанием: он сам рассказывает нам, что надо делать. А мы, если уж решили доставить ему удовольствие, послушно выполняем все требования.

Однако игра – это не только удовольствие и радость для ребенка, что само по себе очень важно. С ее помощью можно развивать внимание, память, мышление, воображение малыша, т.е. те качества, которые необходимы для дальнейшей жизни. Играя, ребенок может приобретать новые знания, умения, навыки, развивать способности, подчас не догадываясь об этом. Родители порой сами предлагают ребенку поиграть в школу, чтобы закрепить навыки чтения; в магазин, чтобы проверить умение считать и т. д.

В нашей книге представлены игры, направленные на умственное развитие ребенка-дошкольника. Их можно разделить на относительно самостоятельные группы. Это игры, развивающие восприятие, внимание, память, мышление и творческие способности. Особая группа игр поможет подготовить ребенка к школе. Для детей каждой возрастной группы (от 3 до 6 лет) предлагаются все эти виды игр.

Игры, направленные на развитие восприятия, формируют у ребенка умение анализировать предметы по таким признакам, как цвет, форма и величина. К концу дошкольного возраста дети могут свободно ориентироваться в 7 цветах спектра, различать их оттенки по насыщенности и цветовому тону. Они должны знать основные геометрические формы (круг, овал, квадрат, прямоугольник и треугольник), уметь подбирать по образцу или по названию предметы определенной формы. Знание такого признака предмета, как величина, выражается в том, что ребенок может расположить 8–10 палочек, кружков или других одинаковых предметов разной величины в порядке ее убывания или возрастания, назвать основные градации величины предметов по 3 измерениям (длина, ширина, высота). Следующая группа игр направлена на развитие внимания. Предлагаемые игры формируют у ребенка умение сосредоточиваться на определенных сторонах и явлениях действительности. (Без сосредоточения невозможно выполнить любую, даже самую простую работу.)

Основные свойства внимания, которые формируются уже в дошкольном возрасте,– это его устойчивость, переключение и распределение. Устойчивость внимания означает способность длительно сосредоточиваться на чем-нибудь. К концу дошкольного возраста дети могут заниматься одним и тем же видом деятельности до 1–1,5 часа. Переключение внимания представляет собой способность переходить от одной деятельности к другой, от одного занятия к другому. О распределении внимания мы говорим тогда, когда человеку приходится действовать сразу с двумя или несколькими предметами. Старший дошкольник в состоянии распределять внимание между 6–7 предметами. В дошкольном возрасте происходит постепенный переход от непроизвольного внимания к произвольному. Непроизвольное внимание характерно тем, что оно вызывается новыми, привлекательными и интересными в данный момент для ребенка предметами. Произвольное внимание предполагает умение сосредоточиваться на задании, даже если оно не очень интересно.

Следующая группа игр направлена на развитие памяти, которая так же, как и внимание, постепенно становится произвольной. Ребенок старшего дошкольного возраста уже может ставить себе цель – запомнить что-либо и с большим или меньшим успехом подбирать средства для выполнения этой цели, т. е. средства, облегчающие процесс запоминания.

Все мы знаем, что цвета спектра легче запоминаются по первым буквам фразы «Каждый охотник желает знать, где сидит фазан». Таким маленьким секретам можно научить и дошкольников. И помогут вам в этом игры по развитию памяти.

Развитие мышления ребенка происходит при условии овладения им тремя основными формами мышления: наглядно-действенным, наглядно-образным и логическим. Наглядно-действенное мышление– это мышление в действии. Оно развивается у младших дошкольников в процессе действий с различными предметами, игрушками Основная форма мышления дошкольника – наглядно-образное мышление – т. е. такая организация образов, которая позволяет выделять самое существенное в предметах, а также видеть соотношение их друг с другом и соотношение их частей. Ребенок должен научиться пользоваться различными планами, схемами. К концу дошкольного возраста у детей начинают складываться элементы логического мышления, т. е. формируются умения рассуждать, делать умозаключения в соответствии с законами логики.

Развитие творческих способностей ребенка подразумевает развитие воображения и гибкого, нестандартного мышления. Творчество во многом определяется умением выражать свои чувства, представления о мире различными способами. А для этого надо научиться видеть в каждом предмете разные его стороны, уметь, отталкиваясь от отдельного признака предмета, строить образ; не только свободно фантазировать, но и направлять свою фантазию, творческие возможности на решение разных задач.

И наконец, игры, помогающие подготовить ребенка к школе. Это игры, которые развивают у малыша элементарные математические представления, знакомят его со звуковым анализом слова, готовят руку к овладению письмом. Почти для каждой игры даются варианты упрощенного или усложненного ее проведения. Поэтому, организуя игры с ребенком, внимательно присмотритесь к нему, оцените его индивидуальные особенности. Если он быстро и легко справляется с заданиями, можно предлагать ему более сложные и, наоборот, в случае затруднений, лучше подольше задержаться на простых. Ни в коем случае нельзя форсировать выполнение заданий, упрекать малыша в том, что он что-либо не умеет, даже если это с легкостью делают его сверстники.

Важно не только научить ребенка чему-либо, но и вселить в него уверенность в себе, сформировать умение отстаивать свою идею, свое решение. Особенно это касается выполнения творческих заданий, которые обычно имеют несколько решений и которые не предполагают жесткой оценки: «верно – неверно». Нужно научить ребенка принимать критику без обид и выдвигать новые идеи.

И опять-таки тут важны индивидуальные черты ребенка. Если он смел и уверен в себе, можно начинать учить его критически оценивать свои ответы. Если застенчив, нерешителен, лучше сначала подбодрить его и поддержать любую инициативу. Если малыш стремится быстро менять задания, отделываясь первым попавшимся ответом, то хорошо бы заинтересовать его заданием, научить находить в нем новые детали, насыщая знакомое новым содержанием. И наоборот, если, выполняя игровое задание, ребенок «увязает» в бесконечных деталях, что мешает ему двигаться вперед, лучше помочь ему выбрать один вариант, оставив все лишнее в стороне, потренировать в умении переходить от одной идеи к другой, что особенно важно при выполнении творческих заданий.

Каждая игра – это общение ребенка со взрослым, с другими детьми; это школа сотрудничества, в которой он учится и радоваться успеху сверстника, и стойко переносить свои неудачи. Доброжелательность, поддержка, радостная обстановка выдумки и фантазии– только в этом случае наши игры будут полезны для развития ребенка. В каждую игру можно играть с одним малышом, а можно и с несколькими. А еще лучше играть всей семьей, хоть на несколько минут откладывая свои дела. Радость, которую вы доставите ребенку, станет и вашей радостью, а проведенные вместе приятные минуты помогут вам сделать добрее и веселее совместную жизнь. Так давайте поиграем!

Мы не можем предоставить возможность скачать книгу в электронном виде.

Информируем Вас, что часть полнотекстовой литературы по психолого-педагогической тематике содержится в электронной библиотеке МГППУ по адресу http://psychlib.ru. В случае, если публикация находится в открытом доступе, то регистрация не требуется. Часть книг, статей, методических пособий, диссертаций будут доступны после регистрации на сайте библиотеки.

Электронные версии произведений предназначены для использования в образовательных и научных целях.

Источник

Математического развития

Содержание

‘ Чего на свете не бывает? Книга для воспитателей детского сада и родителей. / Под ред. О. М.Дьяченко,Е. Л. Агаевой.— М.: Просвещение, 1991.

(планки-вкладыши «Елочки», «Матрешки» и т. п.); пространст­венные отношения иод, на, рядом, около, за (изображение двора с домиком, деревьями, забором, скамейкой и другими предметами и персонажа (например, котенка), которого можно располагать у данных объектов согласно указаниям).

Таким образом, в младшем возрасте значимым является раз­витие замещения (ознакомление детей с возможностью обозначе­ния (замещения) некоторого содержания); при этом важно орга­низовать сопоставление объекта и модели (заместителя), обратить внимание детей на их сходство (в данном возрасте — по внешним признакам: размеру, форме, цвету).

В среднем возрасте использование модели целесообразно, так как оно позволяет систематизировать чувственный опыт выделе­ния признаков предметов, выступает средством их самостоятель­ного познания, способствует развитию умений моделирования. Основной задачей данного возраста является освоение детьми не­которых простых моделей и познание с их помощью свойств и отношений. Модель выступает опорой действий, средством акти­визации обследования объекта.

В играх с детьми 4—5 лет успешно используются сенсорные и простые понятийные модели (наглядно-образной формы вы­ражения), которые применяются в процессе выделения школь­никами свойств, установления различных отношений (графы; модели «Части суток», «Вчера — сегодня — завтра»; планы про­странства помещения; схемы сложения построек; геометриче­ские фигуры как модели формы; сенсорные модели с обозна­чением свойств для рассматривания и описания предметов, сим­волы для группировки объектов по заданным в модели признакам и др.).

Развитию умений использовать модель для освоения разнооб-азных свойств и отношений в процессе рассматривания, описа­ния, сравнения предметов способствует организация проблем­но-игровых ситуаций, упражнений, игр («Составь картинку», «Отгадки»), включающих рассматривание предметов по сенсор­ной модели. Детям предлагается составить описание предмета с помощью карточек-символов, рассказать о предмете с опорой на последовательность заданных символов и т. п. (илл. 62). Ис­пользуются предметно-схематические модели, отражающие раз­личные свойства. Модель выступает образцом, в котором зада­на последовательность обследования предмета, и опорой для вы­деления значимых свойств. Варьирование числа предметов (6—7 шт.) и содержания обозначений в них (форма, размер, ко­личество, характер поверхности, прочность, упругость, прозрач­ность и др.) позволяет избежать формирования стереотипных умений использования моделей.

Дети осваивают простые модели и используют их в установле­нии различных отношений. Традиционно используются игры с ориентировкой на плане («Куда залетела пчела?», «Кукла Маша

Усложнение данных игр (по сравнению с играми для младше­го возраста) включает:

тинке и две модели (расположение данных предметов, выражен­ных заместителями (разными по размеру прямоугольниками)). Одна модель — с адекватным расположением заместителей пред­метов на картинке. Другая не соответствует пространственному расположению предметов относительно друг друга. Ребенку необ­ходимо сопоставить картинку и модели. Игра-упражнение «Не­обычный компьютер» включает воспроизведение посредством модели заданного размерного соотношения. Ребенку предлагает­ся воспроизвести определенное, заданное размерное соотноше­ние между двумя предметами (например, елками). Используется набор предметов (елок) разного размера и модель «Экран», пред­ставляющая собой систему координат (илл. 64), где на одной оси — обозначения цветов, а на другой — предметы. Ребенок вы­бирает задуманное соотношение предметов, подбирая предмет по заданным параметрам (например, елка должна быть шириной в один столбец (красный цвет), высотой — до символа «квадрат»).

Дети 4—5 лет осваивают более обобщенные модели в их раз­личных функциях (средства выражения, измерения отношений); используют варианты мерок, заместителей; совместно со взрос­лым изготавливают шкалы проявления свойств (шкалы прозрач­ности, шероховатости); экспериментируют с моделями («Изме­рим колкость иголок ежика шкалой шероховатости», «Чистые ли окна в группе? (шкала прозрачности)» и др.).

Для старшего дошкольного возраста характерно освоение раз­личного вида моделей (преимущественно понятийного содержа­ния, графических — по форме выражения), а также познание эле­ментов знаково-символических систем (система нумерации),

стремление понять правила построения системы геометрических фигур, систем и мер величин (мер измерения размера, простран­ства, массы, объема и т. п.). Основной задачей данного возраста является развитие самостоятельного опосредованного познания свойств и отношений и повышение осознания семиотической функции.

Используются графические и знаковые модели, такие как ка­лендарь года, счеты, модель «Часть — целое» Н. И. Непомнящей, круги Эйлера—Венна, классификационные деревья. Усложняется и задача по развитию моделирования, предполагающая становле­ние умений вносить изменения в освоенные модели и создавать (составлять) модели (чертить планы пространства комнаты, участка; основы для игры «Морской бой» и т. п.).

Старшие дошкольники осваивают использование модели как опоры действий для выделения и удерживания основания группи­ровки предметов и установления связей, и в результате этого мо­делирование становится способом познания (Л. А. Венгер).

Используются методы и приемы, активизирующие самостоя­тельное применение моделей и моделирование отношений, зави­симостей. Например, в ходе развития пространственных пред­ставлений воспитатель предлагает детям продумать вариант пере­становки мебели в группе. Дошкольникам сообщаются заданные условия: столы для изодеятельности должны стоять у окна, круг­лый стол должен стоять так, чтобы к нему можно было легко под­ходить со всех сторон и т. п. После обсуждения первых предложе­ний обозначается проблема — невозможно практически прове­рить все предложения детей. В ходе обсуждения дошкольники подводятся к возможности моделирования перестановки на плане; определяются способы создания плана, предметы, которые будут представлены на нем; организуется проектная деятельность детей.

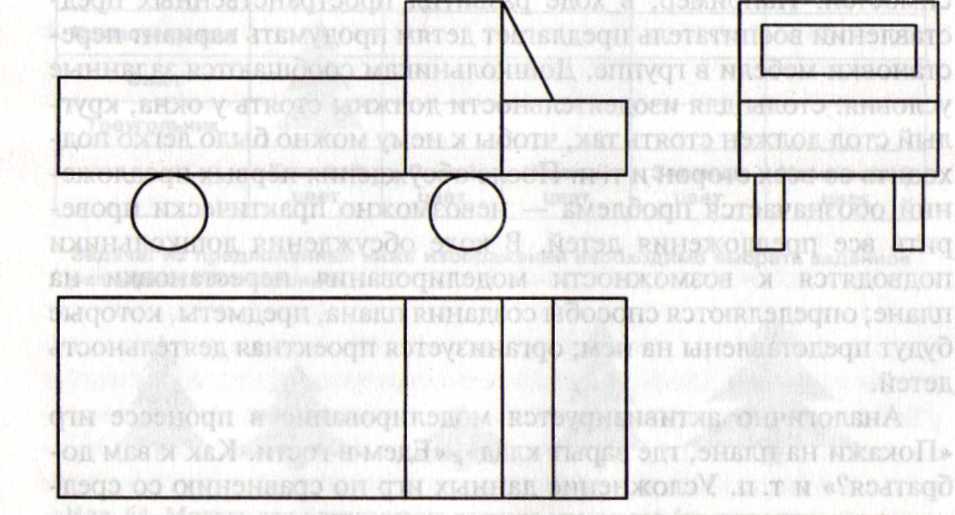
Илл. 65. Модель машины в трех проекциях (вид сбоку, спереди и сверху)

В процессе освоения временных отношений старшие до­школьники активно используют календарь года, объемную мо­дель частей суток, модель часов и т. п. Например, после ознаком­ления с календарем можно организовать игры и обсуждения: «Сколько месяцев (дней) осталось до Нового года? Дня рожде­ния?», «Посчитай, сколько дней рождения детей будет до Нового года», «Сколько дней в каждом месяце?», «Есть ли в этом году 29-е февраля?» и т. п. Календарь позволяет наглядно и схематизирова­но представить иерархию временных отрезков и активизировать детскую деятельность по установлению временных отношений. Старшие дошкольники привлекаются к изготовлению моделей: приклеивают цветные секторы — обозначения дней недели; при­думывают символы — обозначения событий «жизни группы» на календаре-ватмане и т. п. Пониманию обобщенности данных мо­делей способствует сравнение различных календарей (отрывных, настенных с муфтой, карманных и т. п.): при различной форме представления информации не изменяется содержание, т. е. пред­ставленные временные эталоны.

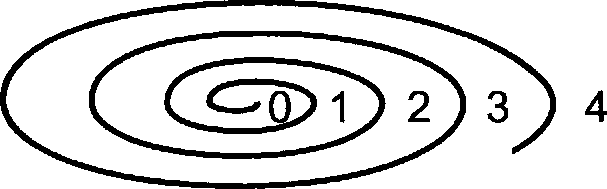
В процессе усвоения количественных отношений и представ­лений о числе организуются игры и упражнения с различными эквивалентами, наглядными моделями («Домики чисел» с целью освоение состава числа), «Дроби» М. Монтессори, палочки Кюи-зенера, доски-дюймовки Е. И. Тихеевой и т. п.); с моделями «Ма­тематический завиток» (илл. 66), «Числовой луч» и т. п.

Илл. 66. Модель «Математический завиток» (Ф. Папи)

Создаются ситуации, требующие воссоздания и дополнения детьми освоенных моделей. Например, в игре «Разместим жиль­цов на этажах» возможно создание модели-схемы дома с несколь­кими этажами и использование заместителей-«жильцов» для мо­делирования условия задачи; в ситуации «Какая кошка сидит выше?» используются модель-схема «дерева» и заместители «кошек»; в ситуации «Кто из детей самый высокий, если. » при­меняются полосы разной высоты для моделирования отношений; в ситуации «Как посадить три цветка у треугольной башни, чтобы у каждой стены росло по два?» используются модель башни — тре­угольник и фишки — заместители цветков. Дошкольники моде­лируют условие на предметах (элементах модели) и «перебирают» варианты решения.

Для успешного использования моделей в данном возрасте не­обходима организация игр и упражнений, способствующих по­вышению понимания детьми семиотической функции и развитию умений моделирования:

• игры и упражнения, способствующие развитию замещения и декодирования символов: «Придумай, как с этим можно поиг­рать?», «Подбери знак-символ к предмету, явлению» (зоопарк, театр кукол, булочная, солнечная погода, сильный снег, многоугольники, утро — день — вечер — ночь и т. п.); «Соста­вим рассказ по волшебным картинкам» (декодирование изоб­ражений некоторых эпизодов рассказа, сказки); «Рисунок для другого» (разработки Е. В. Филипповой, Е. А. Бугрименко (1975); ребенку предлагается нарисовать символы-подсказки для запоминания слов для детей другой группы, используя правила означения) и др. Так, в игре «Разложи картинки» де предмета); «Секреты» 1 (рисование плана пространства и обо­значение на нем загаданного места или предмета); «Составим план комнаты с помощью необычных фигур» (используются более условные заместители, например круги разного размера; ребенок вынужден ориентироваться на пространственные от­ношения, а не на форму заместителя); • проблемные ситуации, способствующие пониманию некото­рых правил моделирования, освоению семиотической функции (правила обозначений, условность знака, возможность пред­ставления информации в разной форме, схематичность и т. п.). Следует отметить, что познание элементов знаково-символи-ческих систем проводится на ознакомительном уровне и включает развитие интереса к овладению ими в более старшем возрасте.

«Заданность» содержания модели может привести к шаблон­ности представлений. Например, наблюдается отсутствие попы­ток установить отношения без модели (своеобразное «ожидание» применения модели), переключение на игру с ней. Данные про­явления преодолимы за счет варьирования содержания модели и игр с нею, создания разнообразной мотивации ее применения, ор­ганизации различных форм детской деятельности (совместных со взрослым игр, упражнений с использованием модели, развива­ющих ситуаций, самостоятельной деятельности в условиях насы­щенной моделями и объектами предметной среды), использова­ния дополнительных приемов (обязательное применение модели и предмета, их «пошаговый» анализ и сопоставление, создание промежуточных, более конкретных и наглядных моделей, различ­ных по форме выражения и содержанию).

Преимуществами использования модели в познании дошкольни­ками являются: возможность формирования как представлений, так и действий моделирования, развитие интереса к познанию; представление информации в наглядной, схематизированной форме, облегчающей ее переработку; возможность организации практических действий с ее элементами (что соответствует доми­нированию наглядно-действенного, наглядно-образного мышле­ния в дошкольном детстве); применение модели в ходе освоения различного содержания, а следовательно, формирование

Вопросы и задания для самоконтроля

© Раскройте основные положения концепции Л. А. Венгера и проиллюстрируйте их играми, упражнениями с использовани­ем моделей.

© Выделите линии усложнения опыта опосредованного позна­ния дошкольниками свойств и отношений.

© Сформулируйте задачи по развитию опосредованного позна­ния свойств и отношений в дошкольном возрасте.

© Обобщите требования к использованию моделей в каждой возрастной группе.

© Определите критерии для анализа развития моделирования в старшей группе ДОУ.

4.3. Реализация идеи интеграции в логико-математическом развитии дошкольников

Интеграция (лат. integraio — восстановление, восполнение; целый) понимается как сочетание и взаимообогащение некоторо­го содержания за счет качественных изменений связей между со­держательными разделами; состояние связывания отдельных дифференцированных частей и функциональных систем в целое, а также процесс, ведущий к такому состоянию.

Например, освоение дошкольниками формы, размерных отно­шений и пространства интегрировано, что соответствует как воз­растным возможностям детей, так и специфике самих математи­ческих категорий (взаимосвязь размерных и пространственных по­казателей). С этой целью разрабатывались познавательно-игровые пособия, ориентированные на обогащение опыта интегрированно­го освоения дошкольниками представлений и умений. Яркими примерами являются пособия «Дары» Ф. Фребеля, «Доска-дюй­мовка» Е. И. Тихеевой, игры с лучинами и на плоскостное модели­рование, серия игр «Кубики для всех», «Прозрачный квадрат», раз­нообразные конструкторы (например, «Лего» и др.).

В процессе конструирования построек (домов, улиц и т. п.) дети осваивают пространственное расположение деталей на плос­кости и в трехмерном пространстве, пространственные отноше­ния между ними; определяют размерное соотношение всей по­стройки и ее элементов, а также количество недостающих элемен­тов устанавливают отношение часть — целое при объединении деталей и т. п. Осваиваемые представления через необходимую дифференциацию представляются детям интегрированно (це­лостно и взаимосвязано), через практические действия и в форме игры. Приобретенный опыт качественно отличается от «обычно­го» раздельного познания данных свойств и отношений: ребенком осваиваются взаимосвязи свойств и отношений, их преобразова­ния, а не отдельные представления и умения (различение, назы­вание и обследование).

Еще одним ярким примером интеграции разделов содержания является переосмысление логики и методических приемов освое­ния представлений о количестве, числе. Число используется для характеристики различных свойств и отношений (им определяет­ся количество углов, сторон, вершин; осуществляется оценка раз­мера, массы, пространственных и временных отношений; число является итогом счета и измерения). Согласно теории В. В. Давы­дова, П. Я. Гальперина, Л. С. Георгиева, для формирования более обобщенного представления о числе необходимо осуществление не только пересчета дискретных множеств (что было представлено в традиционных разработках 30—60-х гг. XX в. в области матема­тического развития дошкольников), но и измерения веществ.

Условно можно также выделить несколько направлений ин­теграции логико-математического развития дошкольников с други­ми направлениями их развития (своеобразная «междисциплинар­ная интеграция»).

Существуют образовательные программы, основанные на принципе интеграции, а также разработки конкретных методов и приемов, ориентированных на данную задачу.

Например, в рамках образовательной программы «Радуга» в процессе освоения математического содержания предусматрива­ется обогащение представлений детей об окружающей дейст­вительности за счет использования элементов географической, астрономической, экономической, художественно-эстетической, социально-нравственной направленности. Математические пред­ставления и действия выступают при этом средством освоения мира, «инструментом» познания.

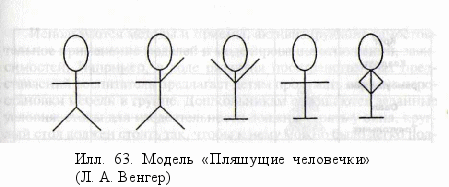
На доступных примерах показана взаимосвязь математиче­ских категорий, событий и явлений мира (как бы «математика в окружающей действительности», математика в сочетании с эсте­тическими, познавательными, эмоционально-образными цен­ностными моментами). Например, детям предстоит «поиск явле­ний (физических, химических, биологических, эстетических, со­циальных), в которых проявляет себя данное свойство или отношение». Так, дошкольники в процессе освоения числа 1 об­суждают, что в единственном числе встречаются Земля, солнце, мама, каждый из нас, произведения искусства и т. п.; при изуче­нии числа 4 — четыре части суток, четыре сезона, четыре части света, четыре угла у квадрата и прямоугольника, четыре конечно­сти у животного и т. п. Содержание различной направленности как бы группируется по заданной категории (например, по числу) и насыщается в том числе мифологической информацией.

Значимо, что идея интеграции реализуется и посредством со­четания познавательной, творческой и игровой деятельности детей. Например, предполагается «поиск „явлений» свойства в предметном мире, в природе и искусстве»; организация изобрази­тельной деятельности, в которой отражаются впечатления детей от освоенного; ознакомление с представленностью данной кате­гории в различных видах искусства (ритм в музыке, движении, декоративном искусстве, литературе).

Помимо интеграции содержания, реализация данного раздела включает также использование методов и приемов, обеспечива­ющих его эмоционально-образное представление (театрализации математической направленности, использование необычных при­емов (например, в процессе наблюдения горения свечей осваива­ется состав числа и т. п.)).

В ряде разработок и исследований выделены возможности ин­теграции логико-математического и познавательно-речевого раз­вития дошкольников, и в частности логико-математического и экологического развития.

Например, изменения в природе диктуют разделение суток на четыре части (утро — день — вечер — ночь), сезоны, цикличность (год). Богатство природных объектов создает условия для эффек­тивного освоения многообразия форм, размеров, пропорциональ­ных соотношений, симметрии и асимметрии и т. п. (листья, ле­пестки цветов, плоды разных форм и размеров; симметричное — асимметричное расположение побегов и т. п.).

Идея интеграции основана на том, что в процессе освоения экономических представлений «востребованы» разнообразные математические действия (счет, измерение, вычисление); также создаются проблемные ситуации, для решения которых дети стре­мятся устанавливать разнообразные отношения (количественные, размерные и т. п.), анализировать условие, рассуждать. Идеи дан­ной интеграции были представлены в работах Е. И. Тихеевой, А. М. Леушиной, А. А. Смоленцевой и др.

В данном аспекте разрабатываются технологии обогащения экономических представлений у дошкольников, основанные на интеграции с логико-математическим содержанием (А. А. Смо­ленцева. «Введение в мир экономики, или Как мы играем в эко­номику»). Технологии направлены на уточнение, конкретизацию и обобщение некоторых представлений экономической направ­ленности, развитию умений и качеств (бережливость, хозяйст­венность, аккуратность, заботливое отношение к окружающим предметам и т. п.). В процессе освоения дошкольниками пред­ставлений о ресурсах, доходах-расходах, бюджете, выгодных пред­ложениях, экономически правильном поведении (на доступных примерах из опыта семьи) создаются ситуации, способствующие развитию математических представлений и действий. Подробные идеи интеграции представлены и в разработках А. Д. Шатовой, Е. А. Сидякиной и др.

В процессе освоения краеведческих представлений математи­ческое содержание может быть «востребованным» и способство­вать более дифференцированному восприятию исторических фактов, культурных традиций, художественно-эстетических до­стопримечательностей (например, сообщение информации о мас­се и размере Гром-камня и обсуждение фактов, связанных с па­мятником Петру I; определение толщины стен Петропавловской крепости в связи с их функциональным назначением; измерение длин различных мостов города и установление связи результатов с шириной соответствующих рек и т. п.). При этом такая интегра­ция не должна приводить к нивелированию эстетической и куль­турной ценности изучаемых объектов.

В ряде методических разработок предусматривается «насыще­ние» процесса освоения краеведческих представлений математи­ческим содержанием; математические действия и представления являются своеобразным инструментом, помогающим уточнить знания о достопримечательностях города. Например, детям пред­стоит решить логические задачи на поиск лишнего, арифметиче­ские задачи, содержательной стороной которых являются некото­рые интересные факты из истории и культуры города; осущест­вить решение примеров и через соотнесение ответа (числа) и буквы — узнать названия рек; решить ребусы, загадки о городе, в которых используются математические данные и т. п. (3. А. Серо­ва. Знакомлюсь с математикой. Пособие для подготовки детей к школе, 2000; Петербургский задачник для малышей, 2003).

В практике детских садов возможна интеграция в форме орга­низаций следующих детских исследовательских и информацион­ных игр-проектов.

• «Архитектура города» (включает освоение размерных от­ношений, формы, пропорции, симметрии — асимметрии в архитектуре и математике; осуществление счета (колонн, этажей зданий); установление связей между этажами, разме­рами домов)).

• Организация экскурсий в город, в процессе которых предсто­ит найти (заметить) необычное по форме (размеру, числу); найти объекты, которых где-то находится по 2 (3—5). Напри­мер, можно предложить упражнение: «Где спряталось число 2 (3, 4, 5)?» (возможные ответы: два памятника у Казанского со­бора, два крыла у Ангела — символа Петербурга, две Ростраль­ные колонны, две колонны у здания, два одинаковых поста­мента, двойняшки в коляске, двойка на номере у машины). Другой пример: «Найти объекты необычного (оригинального, интересного) размера» (высокий шпиль, длинный балкон, вы­сокий пешеход, длинная машина — лимузин); редкой формы (постамент памятника необычной формы, круглое окно под крышей старинного дома, зигзагообразная клумба). Результа­ты обсуждения можно записывать, зарисовывать в альбоме «Путешествия по любимому городу».

Логико-математическое и речевое развитие дошкольников

Интеграция логико-математического и речевого развития ос­нована единстве решаемых в дошкольном возрасте задач. Разви­тие классификации, сериации, сравнения, анализа осуществляет­ся в процессе игр с логическими блоками, веществами, наборами геометрических фигур; в ходе выкладывания силуэтов, выделения отличий и сходства геометрических фигур и т. п. В процессе раз­вития речи активно используются упражнения и игры, предусмат­ривающие данные операции и действия в ходе установления ро­до-видовых отношений (транспорт, одежда, овощи, фрукты и т. п.) и последовательностей событий, составления рассказов, что обеспечивает сенсорное и интеллектуальное развитие детей.

Используются разнообразные литературные средства (сказ­ки, истории, стихотворения, пословицы, поговорки). Это своего рода интеграция художественного слова и математического содер­жания. В художественных произведениях в образной, яркой, эмо­ционально насыщенной форме представлены некоторое познава­тельное содержание, «интрига», новые (незнаковые) математи­ческие термины (например, тридевятое царство, косая сажень в плечах и т. п.). Данная форма представления очень «созвучна» возрастным возможностям дошкольников.

Широко используются сказки и рассказы, в которых сюжет часто построен на основе некоторого свойства или отношения (например, сюжет «Маша и медведи», в котором смоделированы размерные отношения — серия из трех элементов; сказки по типу «гномы и великаны» («Мальчик-с-пальчик» Ш. Перро, «Дюймо­вочка» Г.Х.Андерсена); истории, моделирующие некоторые ма­тематические отношения и зависимости (Г. Остер «Как измеряли удава», Э. Успенский «Бизнес крокодила Гены» и т. п.). Сюжет, образы персонажей, «мелодика» языка произведения (художест­венный аспект) и «математическая интрига» представляют собой единое целое.

В дидактических целях часто используются произведения, в названии которых присутствуют указания на числа (например, «Двенадцать месяцев», «Волк и семеро козлят», «Три поросенка» и т. п.). В качестве приема применяются специально сочиненные для дошкольников стихотворения, например С. Маршака «Весе­лый счет», Т.Ахмадовой «Урок счета», И.Токмаковой «Сколь­ко?»; стихотворения Э. Гайлан, Г. Виеру, А. Кодырова и др. Дан­ные описания цифр, фигур способствуют формированию яркого образа, быстро запоминаются детьми.

В связи с тем что для освоения некоторых разделов содержания логико-математического развития необходимы опыт движений в пространстве и развитие двигательных механизмов, интересны возможности интеграции развития физической культуры детей и их логико-математического развития.

В результате исследований было доказано, что освоение сис­тем отсчета в пространственных ориентировках связано с измене­нием опыта движений у дошкольников. Освоение «пространст­ва — карты» и «пространства — движения», различение правой и левой рук, основных направлений, дифференцированное воспри­ятие расположения предметов в пространстве основаны на опыте передвижения и движений.

Логико-математическое и художественно-эстетическое развитие

Взаимосвязь логико-математического и художественно-эсте­тического содержания (изобразительной деятельности) проявля­ется в нескольких моментах: единство использования некоторых сенсорных эталонов (форма) и категорий (размер, пропорции, пространственные отношения и т. п.), которые в разных аспектах рассматриваются в данных разделах и освоение которых принци­пиально для обоих направлений; важность некоторых общих за­конов (например, «законов симметрии и асимметрии», передача трехмерного мира средствами рисунка и конструирования, как для математического, так и художественно-эстетического разви­тия детей (С. В. Аранова «Обучение изобразительному искусству. Интеграция художественного и логического», 2004)).

Относительно музыкальной деятельности общность состоит в использовании временных интервалов, освоении таких категорий, как длительность, последовательность, продолжительность, темп, ритм, скорость, высота звука и т. п.; использовании счета для опре­деления количества движений, отсчитывания ритма и т. п.

Вариантом интеграции художественно-эстетического и мате­матического содержания может являться организация следующих видов деятельности.

• Проектная деятельность по теме «Математика в искусстве» (с обсуждением правил симметрии и асимметрии в искусстве и математике; передачи формы, пространства в произведениях искусства; многообразия форм в окружающем мире и спосо­бов их передачи в рисунке, лепной работе; способов передачи перспективы, отражения и т. п.). Более частными вариантами таких проектов могут являться темы «Путешествие Линии и Точки в стране искусства и математики» (предусматривает изучение различных видов линий, образование форм и ис­пользование линии (рисунка) в создании художественного об­раза для передачи настроения, отношения и т. п.); «Загадочная Форма» (в искусстве и математике), «Где же спряталось Про­странство?» (в математике и искусстве) и т. п. При реализации данного направления следует учитывать принцип этичности в трактовке художественных образов и избегать ситуации «раз­рушения» целостного впечатления от произведения искусства (которое может произойти в результате привнесения логико-математической информации). • Коллективная игра-конструирование по теме «Город» (вари­анты: «Улица», «Музей» и т. п.), предполагающая совместное обсуждение с детьми макета построения города и обыгрыва­ние результата. Придумывание макета Красивого города (со­ставление плана города, рисование схемы), планирование улиц, домов; создание схем постройки различных зданий с уче­том функционального назначения и эстетических показателей; определение размеров домов, длин улиц. В процессе констру­ирования внимание детей направляется на размерные свойст­ва, форму, проявление симметрии или асимметрии и т. п. В дальнейшем возможно составление карты уже построенного города с условным обозначением символами достопримеча­тельностей (т. е. осуществление операции кодирования).

Логико-математическое и социально-личностное развитие дошкольников

В ряде исследований намечены пути интеграции логико-мате­матического и социально-личностного развития дошкольников (Л. М. Кларина). Социальный мир является интересным и актив­но познаваемым детьми объектом. В связи с этим Н. Н. Поддья­ков отмечал так называемое «социальное экспериментирование», свойственное дошкольникам. Ребенок пытается выявить и по­знать социальные отношения, определить свое место в системе данных отношений, познать себя как часть мира.

В данном аспекте пониманию собственной уникальности, ин­дивидуальности способствует, наряду с другими показателями, знание ребенком своих возможностей и особенностей. Не случай­но старшие дошкольники любят определять, кто выше в группе (кто быстрее пробежал дистанцию, дальше бросил мяч), какого роста они были раньше; рассматривать одежду, в которой ходили они в раннем возрасте; в доказательство того, что они уже выросли (стали старше), — демонстрировать короткие рукава рубашки и т. п. Для обогащения опыта познания своих возможностей в груп­пе детского сада необходимо наличие ростомера, весов, часов, по­казания которых обсуждаются с детьми.

Вариантом такой интеграции в сочетании с тематическим принципом является также организация освоения детьми содер­жания по темам социальной направленности, в которых обога­щается логико-математический опыт. Например, тема «Мы в детском саду» предусматривает освоение детьми нескольких раз­делов («Кто такие „мы»», «Наши дома, снаружи и изнутри», «Правила, действующие в детском саду и семье»), в содержании которых интегрированы три направления: социальное, естест­веннонаучное и логико-математическое. В логико-математиче­ском аспекте предусматривается освоение временных и количе­ственных характеристик и зависимостей (количество родствен­ников, возраст членов семьи, различия в росте детей и родителей, изменения во времени и т. п.), логических связей, от­ношений и зависимостей; различных средств и способов позна­ния (эталонов, моделей, цифр и т. п.). Проводится обсуждение того, как меняются со временем сам ребенок, его близкие, до­машние растения и животные; кто в семье старший (младший); организуется решение и составление арифметических и логиче­ских задач, в сюжетах которых используются факты из жизни семьи (обобщение родители — дети, родственники, сестры — братья и т. п.). Используются рассматривание фотографий, ил­люстраций, построение родословного дерева (своеобразного аналога модели «классификационного дерева»), построение пла­на детской комнаты и т. п.

Интерес представляет также обогащение и применение дет­ского математического опыта в решении проблемных ситуаций и ситуаций нравственной направленности, возникающих в семье и в группе детского сада. Например, как поровну разделить уго­щение (торт) между шестью гостями; два разных по размеру яб­лока — между двумя детьми; три конфеты — между двумя се­страми и т.п.; рассадить всех вокруг стола, чтобы всем было удобно; набрать необходимое количество воды для заваривания чая (для определенного числа приглашенных). В данных ситуа­циях необходимость поиска приемлемого решения активизиру­ется именно нравственными моментами (не обидеть, помочь, сделать «по справедливости» и т. п.): они стимулируют приме­нение математических представлений и умений и показывают необходимость их освоения.

®* Для современных подходов к процессу логико-математиче­ского развития дошкольников характерно использование идей интеграции как на уровне объединения содержательных раз­делов, так и на уровне установления связей между различными направлениями развития детей.

Использование идей интеграции обеспечивает развитие более обобщенных и системных математических представлений и умений.

Реализация интеграции возможна за счет объединения (вза­имообогащения) некоторых содержательных разделов; ис­пользования специально разработанных на данных идеях по­собий; конструирования форм организации детской деятель­ности; применения методов и приемов, ориентированных на интегративный подход.

© Сформулируйте основные идеи интеграции логико-математи­ческого и других направлений развития дошкольников.

© Дайте обоснование преимуществ и возможных недостатков интегрированного подхода к логико-математическому разви­тию дошкольников.

© Сконструируйте схему-конспект вида детской деятельности с использованием идей интеграции.

Источник