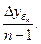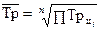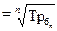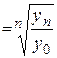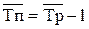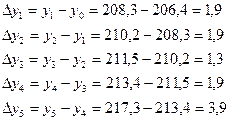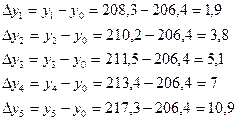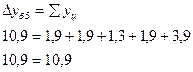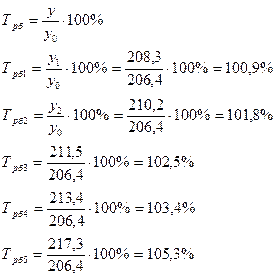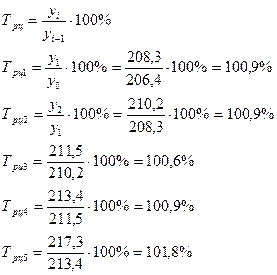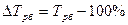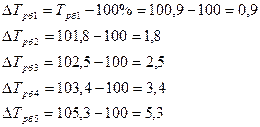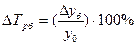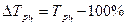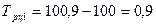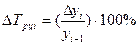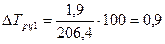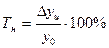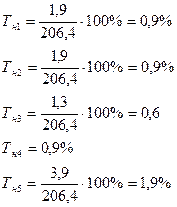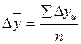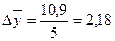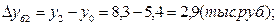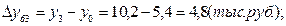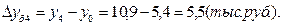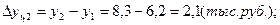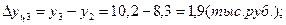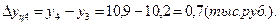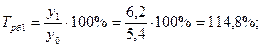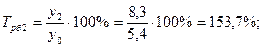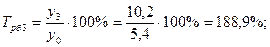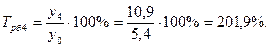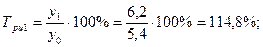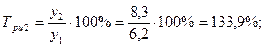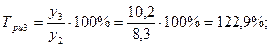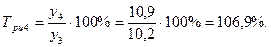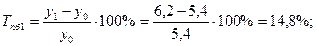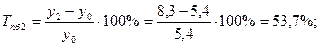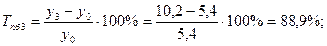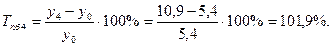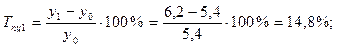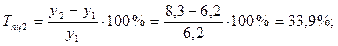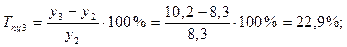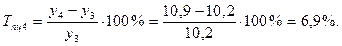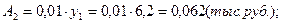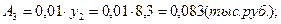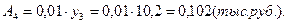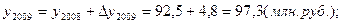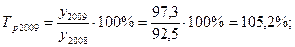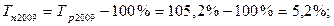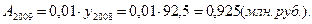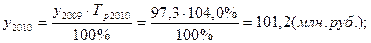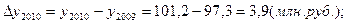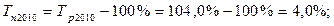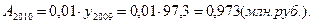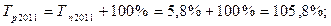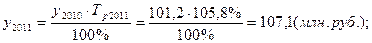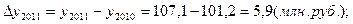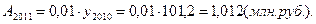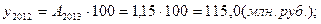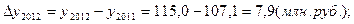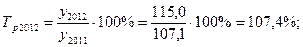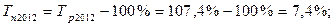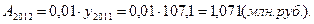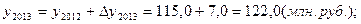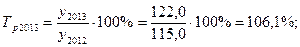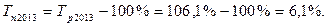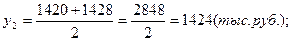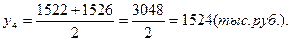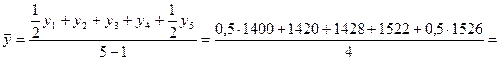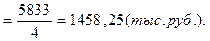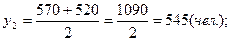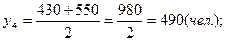коэффициент динамики равен 105 это означает что
Абсолютные и относительные показатели рядов динамики.
Поможем написать любую работу на аналогичную тему
Динамический ряд представляет собой ряд последовательных уровней, сопоставляя которые между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики, к числу которых относятся: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Если сравнению подлежат несколько последовательных уровней, то возможны следующие два варианта сопоставления:
1) каждый уровень ряда динамики сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. В качестве базисного уровня (базы сравнения) выбирается либо начальный уровень ряда динамики или же уровень, с которого начинается какой-то новый этап развития явления. Такое сравнение называется сравнением с постоянной базой;
2) каждый уровень ряда динамики сравнивается с непосредственно ему предшествующим. Такое сравнение называется сравнением с переменной базой.
Показатели динамики с постоянной базой – базисные показатели – характеризуют окончательный результат всех изменений в уровнях ряда от периода, к которому относится базисный уровень, до данного (i-гo) периода.
Показатели динамики с переменной базой – цепные показатели – характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
Абсолютный прирост 
базисный абсолютный прирост: 
цепной абсолютный прирост: 
где 


Темп роста 

базисный коэффициент роста: 
цепной коэффициент роста: 
базисный темп роста: 
цепной темп роста: 
Темп прироста 
базисный темп прироста: 
цепной темп прироста: 
При анализе относительных показателей ряда динамики (темпов роста и темпов прироста) не следует рассматривать их изолированно от абсолютных показателей (уровней ряда и абсолютных приростов) Сравнение абсолютного прироста и темпа прироста за одни и те же периоды времени показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов. Поэтому, чтобы правильно оценить значение полученного темпа прироста, его рассматривают в сопоставлении с показателем абсолютного прироста. Результат выражают показателем, который называют абсолютным значением одного процента прироста. Этот показатель рассчитывают как отношение абсолютного прироста к темпу прироста (в процентах) за тот же период времени:

Рассмотрим расчет вышеуказанных показателей по ряду динамики производства электроэнергии, представленному в табл. 11.4.
Абсолютные и относительные показатели динамики



В основе расчёта показателей ряда динамики лежит сравнительный анализ уровней ряда либо с постоянной, либо с переменной базой сравнения. При постоянной базе сравнения каждый уровень ряда сравнивается с одним и тем же показателем (уровнем), принятым за базу сравнения ( 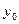
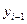
Показатели динамики с постоянной базой сравнения называются базисными, а показатели с переменной базой сравнения – цепными.
1). Абсолютный прирост – это разность между двумя уровнями ряда динамики в исходных единицах измерения:
— базисный:
— цепной:
Он показывает, на сколько данный уровень ряда превышает уровень, принятый за базу сравнения.
По знаку абсолютного изменения делается вывод о характере развития явления: при 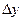
Между цепным и базисным абсолютным приростом существует взаимосвязь: сумма цепных абсолютных приростов равна абсолютному приросту последнего уровня ряда динамики:
2). Темп роста – это отношение двух сравниваемых уровней ряда, может выражаться в виде коэффициента, но чаще в %.
Цепной:
Базисный:
Он показывает, во сколько раз данный уровень ряда превышает уровень базисного периода. Если темп роста > 100%, то идёт увеличение изучаемого уровня по сравнению с базисным или предыдущим, и наоборот.
Между базисным и цепными темпами роста существует взаимосвязь – произведение последовательных цепных темпов роста равно базисному темпу роста последнего уровня ряда динамики:
Частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:
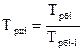
3). Темп прироста характеризует абсолютный прирост в относительных величинах. Определяется двумя способами:
а) как отношение абсолютного прироста к уровню, принятому за базу сравнения:
Базисный:
Цепной:
б) как разность между темпом роста и 100%:
Базисный:
Цепной:
Если уровни ряда динамики сокращаются, то соответствующие показатели темпов прироста будут с минусом, так как они характеризуют уменьшение ряда динамики в процентах.
4). Темп наращивания показывает рост во времени экономического потенциала. Вычисляется делением цепных абсолютных приростов на уровень, принятый за постоянную базу сравнения:
5). Абсолютное значение одного процента приростаопределяется через отношение цепного абсолютного прироста к цепному темпу прироста за соответствующий период:
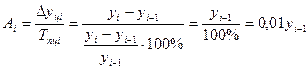
Он показывает, что замедление темпов прироста не всегда сопровождается уменьшением абсолютных приростов.
6). Относительное ускорение представляет собой разность следующих друг за другом темпов роста (прироста) в одном ряду или темпов роста (прироста) за один период в двух смежных рядах динамики:
Относительное ускорение выражается в процентных пунктах роста. В отличие от темпов прироста, которые нельзя ни суммировать, ни перемножать, пункты роста можно складывать, в результате чего получается темп прироста соответствующего периода по сравнению с базисным уровнем.
7). Коэффициент опережения определяется как отношение последующего темпа роста (прироста) к предыдущему или через соотношение темпов роста или темпов прироста за одинаковые периоды времени по двум динамическим рядам:
С помощью коэффициентов опережения сравнивают динамические ряды одинакового содержания, но относящиеся к разным территориям (странам, регионам, районам) или к различным организациям (министерствам, предприятиям), а также ряды разного содержания, характеризующие один и тот же объект (рост потребительских цен и рост среднемесячной зарплаты за одни и те же периоды времени).
Средние показатели
1). Средний уровень ряда динамики– это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности, он характеризует типическую величину абсолютных уровней ряда и зависит от вида ряда динамики:
а) для интервального ряда абсолютных величин с равными периодами (интервалами времени) используется средняя арифметическая простая:
б) для моментного ряда с равными интервалами между датами применяется средняя хронологическая:
в) для моментного ряда с неравными интервалами между датами рассчитывается средняя арифметическая взвешенная:
где 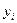
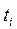
2). Средний абсолютный прирострассчитывается как средняя арифметическая из показателей скорости роста за отдельные промежутки времени:
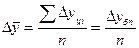
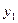
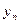
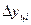
3). Средний коэффициент роста можно определить, пользуясь формулами:
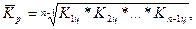
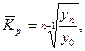
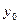
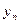
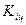
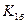
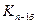
Средний коэффициент роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода времени изменились уровни динамического ряда.
4). Средний темп роста представляет собой средний коэффициент роста, выраженный в процентах:
5). Средний темп прироста:
Таблица 2.1. Уровни (показатели) ряда динамики
| Показатель | Формула | ||||||||||||||||||||||||
| Абсолютный прирост | Δ 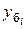 = yi – у0 = yi – у0 | ||||||||||||||||||||||||
| Темп роста | 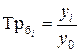 | ||||||||||||||||||||||||
| Темп прироста | 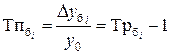 | ||||||||||||||||||||||||
| Абсолютный прирост | Δ 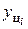 = yi – yi-1 = yi – yi-1 | ||||||||||||||||||||||||
| Темп роста | 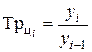 | ||||||||||||||||||||||||
| Темп прироста |
| Показатель | 1985 | 1986 | 1987 | 1988 | 1989 | 1990 |
| Производствен-ная мощность т/сутки | 206,4 | 208,3 | 210,2 | 211,5 | 213,4 | 217,3 |
1. Все аналитические показатели ряда динамики.
2. Взаимосвязь цепных и базисных темпов роста.
3. Привести графическое изображение динамики производственной мощности.
1). Абсолютный прирост
Цепные:
Базисные:
Базисные:
Цепные:
Базисные: 1-й способ:
2-й способ:
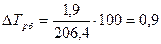
Цепные: 1-й способ:
2-й способ:
4). Темп наращивания:
5). Средний абсолютный прирост:
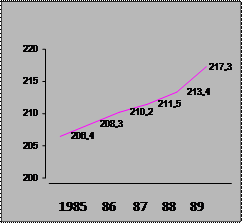 |
Рис. 1. Динамика производственной мощности
Среднемесячные денежные доходы на душу населения по области составили (тыс. руб.):
| 2006 | 2007 | 2008 | 2009 | 2010 |
| 5,4 | 6,2 | 8,3 | 10,2 | 10,9 |
Определить цепные и базисные показатели динамического ряда.
1). Абсолютные приросты:
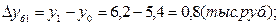
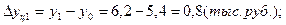
4). Абсолютное значение одного процента прироста:
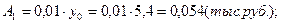
Используя взаимосвязь показателей динамики, определить уровни ряда динамики и недостающие в таблице цепные показатели динамики по следующим данным:
Производство продукции, млн. руб.
По сравнению с предыдущим годом
Решение оформить в таблице.
Исходная таблица приобретает вид:
Производство продукции, млн. руб.
По сравнению с предыдущим годом
Имеются данные об остатках вкладов физических лиц в отделении банка, тыс. руб.:
— на 1 октября – 1522;
— на 1 января следующего года – 1526.
1) средний остаток вкладов населения в каждом квартале;
2) средний годовой остаток вкладов населения.
1). Средние остатки вкладов населения по кварталам:
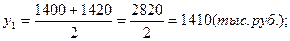
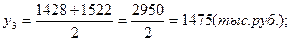
2). Среднегодовой остаток вкладов населения для моментного ряда с равными интервалами определяется по формуле средней хронологической:
Списочная численность работников организации в прошлом году составила: на 1 января – 530 чел., на 1 марта – 570 чел., на 1 июня – 520 чел., на 1 сентября – 430 чел., а на 1 января текущего года – 550 чел. Вычислить среднегодовую численность работников организации за минувший год.
По условиям задачи имеется моментный ряд динамики с неравными интервалами времени: t1=2 месяца, t2=3 месяца, t3=3 месяца, t4=4 месяца.
Среднесписочные численности работников за каждый из этих периодов:
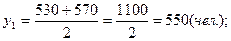
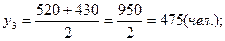
Среднегодовое значение численности работников необходимо рассчитывать по формуле средней арифметической взвешенной:


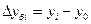
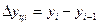
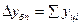
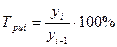
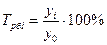
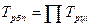
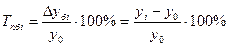
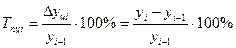
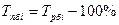
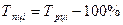
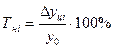
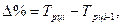
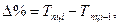
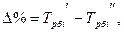
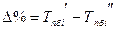
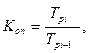
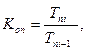
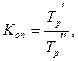
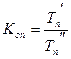

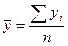
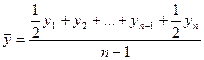
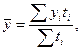
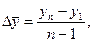
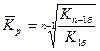
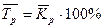
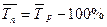
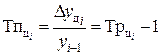
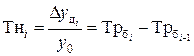
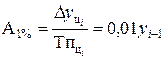
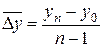 =
=