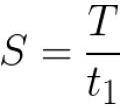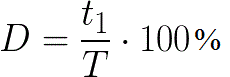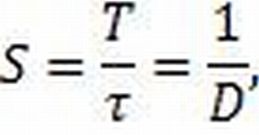коэффициент заполнения скважность что это
Что такое скважность
Одной из важнейших величин в импульсной технике является скважность S. Скважность S характеризует прямоугольный импульс, и определяет то, во сколько раз период импульса T больше его длительности t1. Так, меандр, например, имеет скважность равную 2, поскольку длительность импульса в такой последовательности равна половине его периода: S=T/t1=2.
Как видим, и в числителе, и в знаменателе стоят продолжительности, измеряемые в секундах, поэтому скважность — величина безразмерная. Для справки напомним, что меандр — это такая импульсная последовательность, где длительность положительной части импульса t1 равна длительности его исходного состояния t0.
Величина обратная скважности называется коэффициентом заполнения D. Таким образом, теоретически скважность может изменяться от бесконечности до 1, тогда как соответствующий ей коэффициент заполнения может принимать значения от 0 до 1. Записывать величину скважности часто более удобно, чем коэффициент заполнения в виде дроби.
Например: D=0.5 – коэффициент заполнения меандра, или скважность S=2 – более удобочитаемая запись того же самого. Скважность S=10 соответствует коэффициенту заполнения D=0.1 — имеется ввиду, что продолжительность импульса в 10 раз меньше его периода (суммы его положительной и исходной частей).
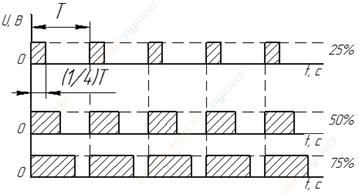
Давайте рассмотрим простой практический пример. Лампочка включается на одну секунду через каждые 59 секунд, затем на 59 секунд гаснет, и так все время повторяется в течение неопределенного времени.
Что это значит? Длительность импульса t1 = 1 секунда, период импульса T = 59+1 = 60 секунд. Следовательно с какой скважностью включается лампочка?
Со скважностью S = 60/1. Скважность 60. Значит коэффициент заполнения равен 1/60, то есть D = 0,01666 или duty cycle 1,66%. В данном примере отчетливо видно, что запись в терминах скважности S = 60 более удобочитаема и точна, чем запись в форме коэффициента заполнения D = 0,01666 или duty cycle 1,666%.
Наконец, еще одно полезное применение скважности. Счетчики-дешифраторы импульсов (типа К561ИЕ8) способны делить импульсную последовательность на отдельные импульсы, здесь снова значение скважности подходит лучше, оно может быть определено через разрядность счетчика и сосчитано (пропорционально количеству импульсов, подсчитанных счетчиком).
Таким образом, даже для цифровой техники оперирование напрямую скважностью импульсов часто оказывается более удобным, чем свойственным принятому в англоязычной литературе коэффициентом заполнения.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Коэффициент заполнения импульсного сигнала. Скважность импульса прямоугольной / сложной формы. Симметричные сигналы
Определение коэффициента заполнения, скважности, обобщенного коэффициента заполнения. Значения для синусоидального и треугольного сигналов. Применение в расчетах. Отношение среднего арифметического значения напряжения к действующему (эффективному) (10+)
[Коэффициент заполнения] = [Длительность импульса (L), с] / [Период следования импульсов (T), с]
Вашему вниманию подборки материалов:
Конструирование источников питания и преобразователей напряжения Разработка источников питания и преобразователей напряжения. Типовые схемы. Примеры готовых устройств. Онлайн расчет. Возможность задать вопрос авторам
Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам
Как мы видим, чем короче импульс, тем меньше коэффициент заполнения. Если длительность импульса стремится к нулю, то и коэффициент заполнения стремится к нулю.
[Скважность] = [Период следования импульсов (T), с] / [Длительность импульса (L), с]
Чем короче импульс, тем больше скважность. Если длительность импульса стремится к нулю, то скважность стремится к бесконечности.
Обобщенный коэффициент заполнения, скважность
Для сложных сигналов также можно ввести понятия коэффициента заполнения и скважности. Будем называть их обобщенными.
[Обобщенный коэффициент заполнения] = [Среднеарифметическое значение напряжения сигнала за период, В] / [Амплитуда сигнала (A), В]
Легко показать, что эта формула для прямоугольных импульсов сводится к приведенной выше.
[Обобщенная скважность] = 1 / [Обобщенный коэффициент заполнения]
Обобщенным коэффициентом заполнения оперируют довольно часто. К понятию обобщенной скважности практически не прибегают.
Для симметричных сигналов описанный выше коэффициент заполнения будет равен нулю, так как среднее арифметическое симметричного сигнала равно нулю. Для анализа симметричных периодических сигналов применяется понятие коэффициента заполнения полупериода. Для его расчета используется формула:
[Обобщенный коэффициент заполнения полупериода] = [Среднеарифметическое значение напряжения сигнала за полупериод, В] / [Амплитуда сигнала (A), В]
Коэффициент заполнения полупериода используется для расчета схем с трансформаторами, катушками индуктивности или конденсаторами. Например, чтобы определить, до какого напряжения за полупериод зарядится конденсатор, нужно посчитать довольно замысловатый интеграл или воспользоваться простой формулой:
[Напряжение на конденсаторе в конце полупериода, В] = [Напряжение на конденсаторе в начале полупериода, В] + [Обобщенный коэффициент заполнения полупериода] * [Амплитуда силы тока, А] * [Длительность полупериода, с]
[Сила тока в катушке индуктивности в конце полупериода, А] = [Сила тока в начале полупериода, А] + [Обобщенный коэффициент заполнения полупериода] * [Амплитуда напряжения, В] * [Длительность полупериода, с]
Обобщенные коэффициенты заполнения для разных распространенных сигналов можно взять из таблиц. Иногда известно не амплитудное, а действующее значение. Тогда полезен будет другой коэффициент: отношение среднего арифметического значения к действующему. С математической точки зрения он равен отношению среднего арифметического к среднему квадратичному.
[Напряжение на конденсаторе в конце полупериода, В] = [Напряжение на конденсаторе в начале полупериода, В] + [Отношение среднего арифметического значения силы тока к действующему] * [Действующее значение силы тока, А] * [Длительность полупериода, с]
[Сила тока в катушке индуктивности в конце полупериода, А] = [Сила тока в начале полупериода, А] + [Отношение среднего арифметического значения напряжения к действующему] * [Действующее значение напряжения, В] * [Длительность полупериода, с]
Для синусоидального сигнала
[Обобщенный коэффициент заполнения полупериода] = 0.637
[Отношение среднего арифметического значения напряжения к действующему] = 0.9
Для треугольного сигнала
[Обобщенный коэффициент заполнения полупериода] = [L, с] / [T, с] / 2
[Отношение среднего арифметического значения напряжения к действующему] = [Корень квадратный из 3] * [L, с] / [T, с] / 2
В литературе нередко понятием ‘Коэффициент заполнения’ обозначают то коэффициент заполнения периода, то коэффициент заполнения полупериода, то отношение среднего значения к действующему. Так что, о чем идет речь, приходится понимать по контексту.
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.
Практика проектирования электронных схем. Самоучитель электроники.
Искусство разработки устройств. Элементная база радиоэлектроники. Типовые схемы.
Конструирование (проектирование и расчет) источников питания и преобра.
Разработка источников питания и преобразователей напряжения. Типовые схемы. Прим.
Зарядное устройство. Импульсный автомобильный зарядник. Зарядка аккуму.
Схема импульсного зарядного устройства. Расчет на разные напряжения и токи.
Широтно Импульсная Модуляция (ШИМ, PWM)
Все микропроцессоры работают с цифровыми сигналами, т.е. с логическим нулем (0 В), или логической единицей (5 В или 3.3 В). Поэтому микропроцессор не может сформировать на выходе промежуточное напряжение. Использование для этих целей внешних ЦАП (www.drive2.ru/b/2558751/) — сложно и задействует сразу много ножек микропроцессора, что неудобно. В этих случаях применяют Широтно-импульсную модуляцию (ШИМ, англ. pulse-width modulation (PWM)) — процесс управления мощностью, подводимой к нагрузке, путём изменения скважности импульсов, при постоянной частоте. Широтно-импульсная модуляция представляет собой периодический импульсный сигнал.
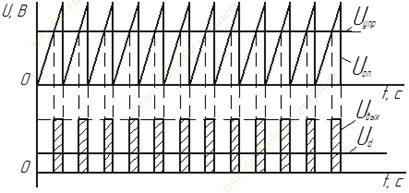
Существуют цифровые и аналоговые ШИМ. Принцип их работы остается одинаковым вне зависимости от исполнения и заключается в сравнении двух видов сигналов:
Uоп – опорное (пилообразное, треугольное) напряжение;
Uупр – входное постоянное напряжение.
Cигналы поступают на компаратор, где они сравниваются, а при их пересечении возникает / исчезает (или становится отрицательным) сигнал на выходе ШИМ.
Выходное напряжение Uвых ШИМ имеет вид импульсов, изменяя их длительность, мы регулируем среднее значение напряжения (Ud) на выходе ШИМ:
Однополярная модуляция означает, что происходит формирование импульсов только положительной величины и имеет место нулевое значение напряжения
Если сформированный таким образом сигнал подать на объект, обладающий фильтрующими свойствами, например, на двигатель постоянного тока или лампу накаливания, то объект будет использовать среднюю мощность сигнала.
Т.е. мощность, потребляемая объектом управления, пропорциональна скважности сигнала ШИМ, при условии, что период импульсов ШИМ на порядок меньше минимальной постоянной времени объекта.
ШИМ может быть встроенным выходом микропроцессора, может быть организована отдельно на выходе микропроцессора с обычным цифровым выходом.
Преимущество использования ШИМ — это легкость изменения величины напряжения при минимальных потерях.
Период тактирования T определяет через какие промежутки времени подаются импульсы.
Длительность импульса — величина показівающая время в течении которого подается сигнал t, с;
Скважность — Соотношение длины импульса (τ) к периоду тактирования (T); пропорционально модулирующей величине. Коэффициент заполнения обычно отображают в процентах (%).
Коэффициент заполнения D – величина обратная скважности.
Несмотря на то, что скважность и коэффициент заполнения могут использоваться в одинаковом контексте, физический смысл их отличается.
Эти величины безразмерны.
PS ШИМ может быть реализован не только при помощи микроконтроллеров, но и на аналоговой базе. Например, простейший ШИМ на основе мультивибратора из двух транзисторов:
Моментные характеристики и период следования импульсов управления — измерение и использование при конструировании систем управления
Главная > Теория > Скважность импульсов
Общеизвестно, что регулировать количество оборотов электродвигателя можно периодическим включением и отключением его от энергосети, кроме того при изменении времени включения и отключения можно задавать дополнительные параметры скорости. Это явление характерно не только для электродвигателя – его действие можно заметить во всех потребителях тока, способных запасать энергию, иначе говоря, инерционных системах.

Скважность
Принцип широтно-импульсной модуляции основан именно на этом эффекте, он нашёл себе достаточно широкое применение при управлении электротехническими устройствами и источниками освещения, где требуется циклическая подача энергии. В английском языке этот принцип получил название – Pulse-Width Modulation.
Чем отличается скважность и коэффициент заполнения импульсов
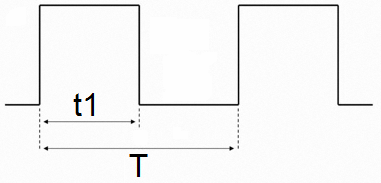
Одной из наиболее важных величин в импульсной электронике – это скважность, обозначаемая латинской буквой S. Она дает характеристику импульсам прямоугольной формы и показывает, как относится их период T ко времени t1. К примеру, коэффициент меандра равен 2, поскольку время t1 в этой последовательности составляет половину периода: S = T / t1 = 2. И в числителе, и в знаменателе находится время, выраженное в секундах. При вычислениях они сокращаются, поэтому коэффициент является величиной, не имеющей единиц измерения.

Генератор скважности
Меандр представляет собой поток импульсов, в котором отрицательные и положительные части имеют одинаковую продолжительность. Инверсия скважности имеет название коэффициент заполнения. Следовательно, скважность способна принимать множество значений от бесконечности до единицы, а рабочий цикл этого же потока импульсов, как еще могут называть коэффициент заполнения, способен принимать значения от 0 до 1. Часто удобней записывать не данный коэффициент, измерение которого производится десятичными дробями, а скважность, которая равна, чаще всего, целому числу. Например: D = 0,5 или S = 2 – эти две записи означают одно и то же, но вторую читать легче. Рабочий цикл S = 10 соответствует показателю D = 0,1 – это означает, что длительность импульса в 10 раз меньше его периода. В широтно-импульсной модуляции (сокращенно, ШИМ) прибор изменяет ширину или продолжительность импульса, при этом будет соответственно изменяться и коэффициент. Частота при этом будет постоянной. В таком случае, чем больше величина, показывающая скважность, тем более узким будет импульс, и, наоборот – при минимальной скважности будет достигаться максимальная ширина. При изучении данного явления просматривается этимологическая связь с словом «скважина» из русского языка: широкая скважина (на самом деле, это промежуток между импульсами в потоке) – положительные части узкие, узкая скважина – положительные части широкие (но свободное пространство между ними мало).
Вам это будет интересно Как заряжается конденсатор
Важно: У англоязычных авторов термин «скважность» не встречается вовсе, а для его замены применяют понятие «рабочий цикл» – аналогичный российскому коэффициенту заполнения (D). Однако в английской литературе он выражается не дробным числом, а процентом. Например, если D = 0,5 в западных пособиях будет указано: D = 50%.






Общая информация
К основным параметрам последовательности импульсов относятся:
Если длительность tu всех импульсов, входящих в состав последовательности, и всех пауз tn постоянна в течение времени, то она называется периодической.
Важным параметром периодического импульсного процесса является скважность импульсов S. Скважность импульсов – это отношение периода следования к длительности импульса, рассчитывается по формуле:
Эффективность S при управлении устройства достигается при стабильной частоте сигнала. Иногда используют обратную величину D – коэффициент заполнения, рассчитывается по формуле:
При равенстве tu и tn скважность равна 2, и сигнал называется меандром. S и D – безразмерные величины, так как время делится на время. В цифровых устройствах применяются импульсы различной формы. Формой импульса называется графическое изображение закона изменения импульсного напряжения во времени. На рис. ниже показаны формы сигналов:

Виды импульсных сигналов
Техническая характеристика формы импульсов связана с количественной оценкой основных параметров импульса, свойств отдельных его участков, которые играют разную роль при воздействии импульса на устройство. На рис. выше изображены идеализированные формы импульса. Из-за переходных процессов в устройствах (формирования и усиления импульсов) существует реальная форма, например, прямоугольного импульса (рис. ниже).

Реальная форма импульса
Основные параметры импульса – это:
Указанные величины считываются между уровнями 0.1 и 0.9 от амплитуды в микросекундах, в зависимости от частоты сигнала. Амплитудные – в вольтах.
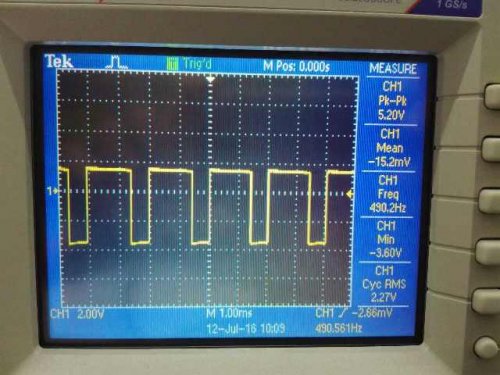
Определить параметры импульсного сигнала можно с помощью осциллографа, частотомера или мультиметра.
Принцип действия
Для формирования прямоугольного колебания в устройствах-модуляторах имеется специальная микросхема-контроллер либо аналоговая микросхема. Подключение происходит посредством цепи на полупроводнике. Полупроводник имеет только два состояния:
Важно! Работа всей цепи зависит от характера колебаний. Следовательно, если лампа подключена через полупроводниковый прибор, она начнёт мерцать с заданной частотой.
Однако, когда частота превышает 50 Гц, из-за особенностей глаз человека, мигание сливается в единое свечение. Но таким образом можно регулировать и яркость свечения. Снижение коэффициента повлечет за собой уменьшение яркости света, выдаваемой лампой.
Подобную схему можно использовать для постоянных двигателей. Уменьшение частоты провоцирует снижение скорости вращения двигателя, а высокие – к большей мощности агрегата.
В аналогичных устройствах применяется полупроводниковый переключатель, который имеет высокую скорость срабатывания и низкую проводимость, поскольку в противном случае устройство может запаздывать.
Формы сигналов
Сигналы различаются по форме и характеристикам:
Вам это будет интересно Подключение к сетям
Важно! Период и частота математически зависят друг от друга. По мере того, как период уменьшается, частота увеличивается, и наоборот.

Синусоид

Меандр

Прямоугольный сигнал
Важно! Сигнал может принимать и положительные, и отрицательные значения, подвергаясь изменениям. В показанном потоке время положительного импульса больше, чем длительность отрицательного импульса, хотя бывает и наоборот.
Расчет коэффициента заполнения печатной платы
Расчет узкого места Читать далее: Конструкторская часть
3.4 Расчет коэффициента заполнения печатной платы
Расчет коэффициента заполнения печатной платы можно сделать по сборочному чертежу платы. Для этого надо измерить площадь, занимаемую элементом вместе с выступающими за корпус выводами.(Посадочное место). В плане (плоскости) все посадочные места можно рассматривать как прямоугольники и окружности. Как известно, площадь прямоугольника равна произведению длины на ширину прямоугольника, а площадь круга
D – диаметр круга, а π – физическая константа, равная 3,14
Расчет следует вести с использованием таблицы 3.4.1
Таблица заполняется, после чего надо сложить все цифры последнего столбца. Таким образом будет найдена площадь, занимаемая всеми элементами схемы S элемент.
Площадь печатной платы — S платы равна произведению ее длины на ширину. Коэффициент заполнения печатной платы
S элемент = 2101,1 мм²
К зап = S элемент / S платы х 100%
К зап = 2101,1 / 4516,2 х 100% = 214,94
Расчет узкого места Читать далее: Конструкторская часть
Информация о работе «Устройство управления вентиляторами компьютера через порт LPT»
Раздел: Информатика, программирование Количество знаков с пробелами: 103194 Количество таблиц: 20 Количество изображений: 3
Похожие работы
Устройство и сборка компьютера
… картриджах. Она производится нескольких цветов, так что простой заменой картриджа можно обеспечить печать многоцветных изображений. 2. ПРАКТИЧЕСКАЯ ЧАСТЬ 2.1 Сборка компьютера Инструкция по сборке ПК. Основные компоненты сборки: 1. Корпус с установленным в нем блоком питания. 2. Материнская плата с документацией к ней. 3. Процессор. 4. Кулер для …
Подключение оборудования к системному блоку
… вопросом в связи с тем, что работе с ними надо учиться специально. На практике подобными клавиатурами оснащают только специализированные рабочие места. По методу подключения к системному блоку различают проводные и беспроводные клавиатуры. Передача информации в беспроводных системах осуществляется инфракрасным лучом. Обычный радиус действия таких клавиатур составляет несколько метров. Источником …
Компьютер как главная технологическая и техническая база информационных систем
… три нажатия клавиши Empowering легко контролировать доступ к данным, настраивать параметры безопасности и быстродействия. Реальные требования к оснащению современных рабочих мест ставят перед информационно-технологическими подразделениями новые задачи по централизации потоков данных и обеспечению высочайшей безопасности и защиты ключевой информации. Компактный и тихий ПК, обладающий значительной …
Сравнительный анализ и оценка эксплутационных характеристик различных терминальных устройств информации в вычислительных системах
Как измерить скважность с помощью формулы
Скважность прямоугольных импульсов S – это отношение периода T ко времени импульса, обозначаемого буквой t1. Также, стоит отметить, что рабочий цикл D – это значение обратное скважности:

Скважность формула
Скважность сигнала – одна из самых важных характеристик в импульсной технике. Ее основные характеристики – это период и время численного значения импульса. Изменяя эти характеристики, можно повлиять на всю цепь.
- коэффициент занятости на дату начала нетрудоспособности что это
- коэффициент затухания в чем измеряется