кольцо мебиуса что это такое
Практически все знают, как выглядит символ бесконечности, напоминающий перевернутую восьмерку. Этот знак называют еще «лемниската», что с древнегреческого означает лента. Представьте себе, что символ бесконечности очень похож на реально существующую математическую фигуру. Знакомьтесь, Лента Мебиуса!
Что такое Лента Мебиуса?
Чтобы понять, о чем идет речь, и как такое может быть, возьмите лист бумаги, вырежьте полоску прямоугольной формы и в момент соединения ее концов перекрутите на 180 градусов один из них, после чего соедините. Разобраться в том, как сделать ленту Мебиуса поможет картинка ниже.
Что же такого примечательного в ленте Мебиуса?
Лента Мебиуса – пример неориентируемой односторонней поверхности с одним краем в обычном трёхмерном Евклидовом пространстве. Большинство предметов являются ориентируемыми, имеющими две стороны, например, лист бумаги.
Чтобы поверить в то, что у петли Мебиуса всего один край – проведите пальцем по одному из граней ленты не прерываясь, и Вы точно так же, как и в случае с раскрашиванием, упретесь в точку, с которой начали движение. Удивительно, не правда ли?
Изучением ленты Мёбиуса и множества других интересных объектов занимается – топология, раздел математики, который исследует неизменные свойства объекта при его непрерывной деформации – растяжении, сжатии, изгибе, без нарушения целостности.
Открытие Августа Мебиуса
«Отцом» открывателем этой необычной ленты признан немецкий математик Август Фердинанд Мебиус, ученик Гаусса, написавший не одну работу по геометрии, но прославившийся преимущественно открытием односторонней поверхности в 1858 году.
Удивительным является тот факт, что ленту с одной поверхностью в тот же самый 1858 год открыл другой ученик Гаусса – талантливый математик Иоганн Листинг, придумавший термин «топология» и написавший серию основополагающих трудов по этому разделу математики. Однако свое название необычная лента все же получила по фамилии Мебиуса.
Есть расхожее мнение, что прообразом модели «бесконечной петли» стала неверно сшитая лента служанкой профессора Августа Мебиуса.
На самом деле, лента была открыта давным-давно еще в древнем мире. Одним из подтверждений служит находящаяся во Франции, в музее города Арль древнеримская мозаика с такой же перекрученной лентой. На ней нарисован Орфей, очаровывающий зверей звуками арфы. На фоне неоднократно изображен орнамент с перекрученной лентой.
«Магия» ленты Мебиуса
Вас порядком удивит результат, ведь вопреки ожиданиям в руках останется не два отрезка ленты, и даже не два отдельных круга, но другая, еще более длинная лента. Это уже будет не лента Мебиуса, перекрученная на 180 градусов, а лента с поворотом на 360 градусов.
У меньшей ленты Мёбиуса будет 1/3 от изначальной ширины ленты, длина L и поворот на 180 градусов. У второй более длинной ленты будет также ширина 1/3 от начальной, но длина 2L, а поворот на 360 градусов.
Зачем нужна петля Мебиуса? Применение
Лента Мебиуса – вовсе не абстрактная фигура, нужная лишь для целей математики, она нашла применение и в реальной повседневной жизни. По принципу этой ленты функционирует в аэропорту лента, передвигающая чемоданы из багажного отделения. Такая конструкция позволяет ей служит дольше в связи с равномерным изнашиванием. Открытие Августа Мебиуса повсеместно исполбьзуется в станкостроении. Конструкцию используют для большего времени записи на пленку, а также в принтерах, использующих ленту при распечатке.
Благодаря своей наглядности, петля Мебиуса дает возможность делать современным ученым все новые и новые открытия. С момента обнаружения удивительных свойств петли по всему миру прокатилась волна новых запатентованных изобретений. Например, значительное улучшение свойств магнитных сердечников, изготовленных из ферро-магнитной ленты, намотанных по способу Мебиуса.
Н. Тесла получил патент на многофазную систему переменного тока, использовав намотку катушек генератора по типу петли Мебиуса.
Лента Мебиуса – широкое поле для Вдохновения
Сложно оценить важность значения открытия петли Мебиуса, которое вдохновило не только большое множество ученых, но и писателей, художников.
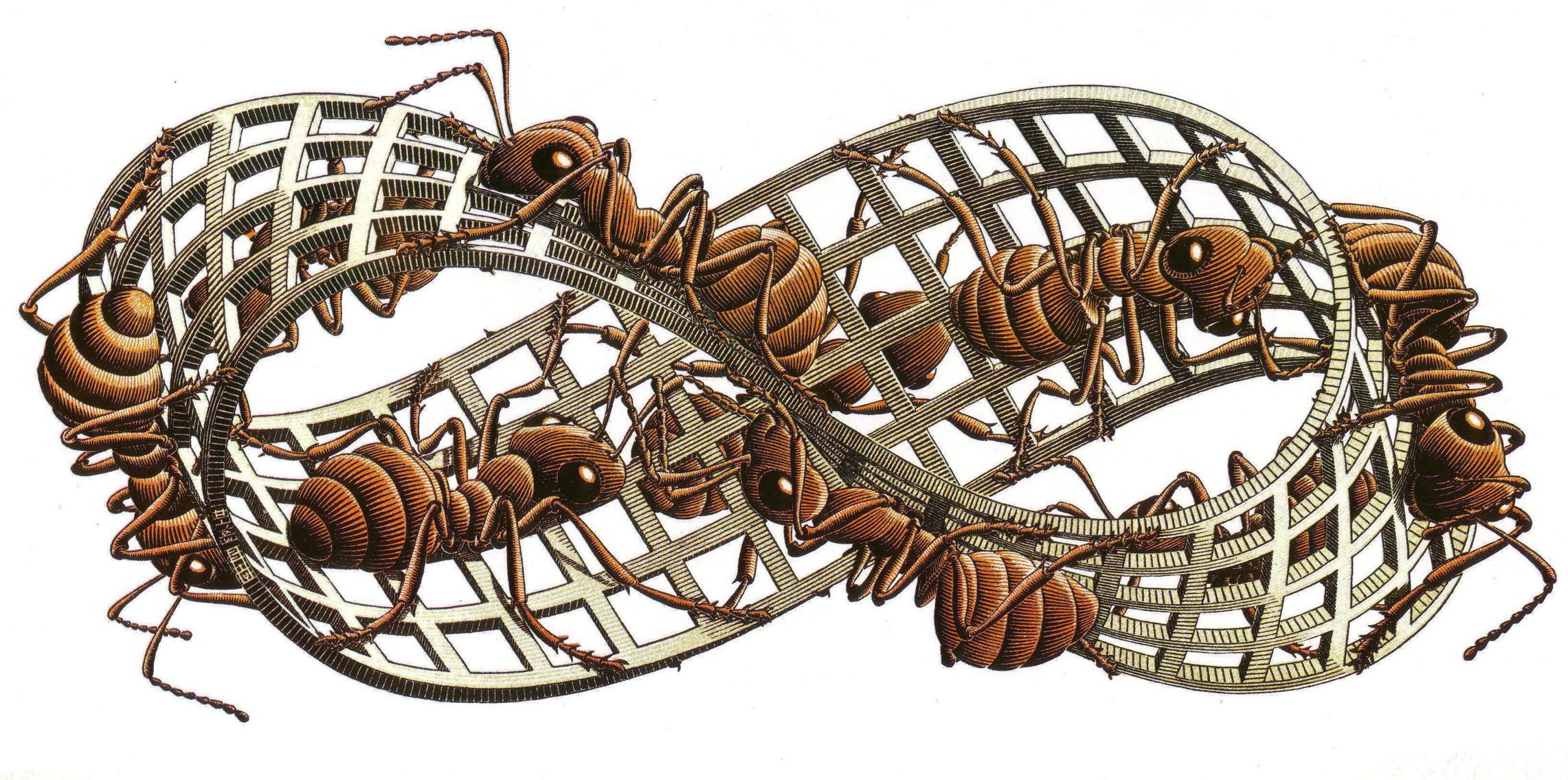
Самой известной работой, посвященной ленте Мебиуса считается картина Moebius Strip II, Red Ants или Красные Муравьи голландского художника-графика Маурица Эшера. На картине представлены муравьи, карабкающиеся по петле Мебиуса с обеих сторон, на самом деле сторона всего одна. Муравьи ползут по бесконечной петле друг за другом по одной и той же поверхности.
Художник черпал свои идеи из статей и трудов по математике, он был глубоко увлечен геометрией. В связи с чем на его литографиях и гравюрах часто присутствуют различные геометрические формы, фракталы, потрясающие оптические иллюзии.
До сих пор интерес к петле Мебиуса находится на очень высоком уровне, даже спортсмены ввели одноименную фигуру высшего лыжного пилотажа.
По произведению «Лента Мёбиуса» писателя фантаста Армина Дейча снят не один фильм. В форме петли Мебиуса создается огромное множество украшений, обуви, скульптур и многих других предметов и форм.
Лист Мебиуса наложил отпечаток на производство, дизайн, искусство, науку, литературу, архитектуру.
Умы многих людей волновала схожесть формы молекулы ДНК и петли Мебиуса. Существовала гипотеза, которую выдвинул советский цитолог Навашин, что форма кольцевой хромосомы по строению аналогична ленте Мебиуса. На эту мысль ученого натолкнул тот факт, что кольцевая хромосома, размножаясь, превращается в более длинное кольцо, чем в самом начале, или в два небольших кольца, но как в цепи продетых одно в другое, что очень напоминает выше описанные опыты с листом Мебиуса.
Есть еще одна более масштабная теория. Вселенная – это огромная петля Мебиуса. Такой идеи придерживался Эйнштейн. Он предположил, что Вселенная замкнута, и космический корабль, стартовавший из определенной ее точки и летящий все время прямо, возвратится в ту же самую точку в пространстве и времени, с которой и началось его движение.
Пока это всего лишь гипотезы, у которых есть как сторонники, так и противники. Кто знает, к какому открытию подведет ученых, казалось бы, такой простой объект, как Лента Мебиуса.
 masterok
masterok
Мастерок.жж.рф
Хочу все знать
Лента Мебиуса, которую также называют петлей, поверхностью или листом, – это объект изучения такой математической дисциплины, как топология, исследующей общие свойства фигур, сохраняющихся при таких непрерывных преобразованиях, как скручивание, растяжение, сжатие, изгибание и других, не связанных с нарушением целостности. Удивительной и неповторимой особенностью такой ленты является то, что он имеет всего одну сторону и край и никак не связаны с ее расположением в пространстве.
Лист Мебиуса является топологическим, то есть непрерывным объектом с простейшей односторонней поверхностью с границей в обычном Евклидовом пространстве (3-мерном), где возможно из одной точки такой поверхности, не пересекая края, попасть в любую другую.
Кто и когда ее открыл?
Такой непростой объект, как лента Мебиуса, был и открыт довольно необычно. Прежде всего отметим, что два математика, абсолютно не связанные между собой в исследованиях, открыли ее одновременно – в 1858 году. Еще одним интересным фактом является то, что оба этих ученых в разное время являлись учениками одного и того же великого математика — Иоганна Карла Фридриха Гаусса. Так, вплоть до 1858 года считалось, что любая поверхность обязана иметь две стороны. Однако Иоганн Бенедикт Листинг и Август Фердинанд Мебиус открыли геометрический объект, у которого была всего одна сторона, и описывают его свойства. Лента была названа в честь Мебиуса, а вот отцом-основателем «резиновой геометрии» топологи считают Листинга и его труд «Предварительные исследования по топологии».
Ленте Мебиуса присущи следующие свойства, не меняющиеся при ее сжимании, разрезании вдоль или сминании:
1. Наличие одной стороны. А. Мебиус в своем труде «Об объеме многогранников» описал геометрическую поверхность, названную затем в его честь, обладающую всего одной стороной. Проверить это довольно просто: берем ленту или лист Мебиуса и стараемся закрасить внутреннюю сторону одним цветом, а внешнюю – другим. Не суть важно, в каком месте и направлении было начато окрашивание, вся фигура будет закрашена одним цветом.
2. Непрерывность выражается в том, что любую точку этой геометрической фигуры можно соединить с любой другой ее точкой, не пересекая границы поверхности Мебиуса.
3. Связность, или двухмерность, заключается в том, что при разрезании ленты вдоль, из нее не получится несколько разных фигур, и она остается цельной.
4. В ней отсутствует такое важное свойство, как ориентированность. Это значит, что человек, идущий по этой фигуре, вернется к началу своего пути, но только в зеркальном отражении самого себя. Таким образом, бесконечная лента Мебиуса может привести к вечному путешествию.
5. Особый хроматический номер, показывающий, какое максимально возможное число областей на поверхности Мебиуса, можно создать так, чтобы у любой из них была общая граница со всеми другими. Лента Мебиуса имеет хроматический номер – 6, а вот кольцо из бумаги – 5.
Сегодня лист Мебиуса и его свойства широко применяются в науке, служа основой для построения новых гипотез и теорий, проведения исследований и экспериментов, создания новых механизмов и устройств.
Так, существует гипотеза, согласно которой Вселенная — это огромнейшая петля Мебиуса. Косвенно об этом свидетельствует и теория относительности Эйнштейна, согласно которой даже полетевший прямо корабль может вернуться в ту же временную и пространственную точку, откуда стартовал.
Другая теория рассматривает ДНК как часть поверхности Мебиуса, что объясняет сложности с прочтением и расшифровкой генетического кода. Кроме всего прочего, такая структура дает логичное объяснение биологической смерти – замкнутая на самой себе спираль приводит к самоуничтожению объекта.
По мнению физиков, многие оптические законы основываются на свойствах листа Мебиуса. Так, например, зеркальное отражение — это особый перенос во времени и человек видит перед собой своего зеркального двойника.
Реализация на практике
В различных отраслях промышленности лента Мебиуса применение нашла уже давно. Великий изобретатель Никола Тесла в начале века изобрел резистор Мебиуса, состоящий из двух скрученных на 1800 проводящих поверхностей, который может противостоять потоку электрического тока без создания электромагнитных помех.
На основе исследований поверхности ленты Мебиуса и ее свойств было создано множество устройств и приборов. Ее форму повторяют при создании полосы ленточного конвейера и красящей ленты в печатных устройствах, абразивных ремней для заточки инструментов и автоматической передачи. Это позволяет значительно увеличить срок их службы, так как изнашивание происходит более равномерно.
Не так давно удивительные особенности листа Мебиуса позволили создать пружину, которая, в отличие от обычных, срабатывающих в противоположном направлении, не меняет направление срабатывания. Применяется она в стабилизаторе рулевого привода штурвала, обеспечивая возврат рулевого колеса в исходное положение.
Кроме того, знак лента Мебиуса используется в разнообразных торговых марках и логотипах. Самый известный из них — это международный символ вторичной переработки. Его проставляют на упаковках товаров либо пригодных для последующей переработки, либо сделанных из переработанных ресурсов.
Источник творческого вдохновения
Лента Мебиуса и ее свойства легли в основу творчества многих художников, писателей, скульпторов и кинематографистов. Самый известный художник, использовавший в таких своих работах, как «Лента Мебиуса II (Красные муравьи)», «Всадники» и «Узлы», ленту и ее особенности — Мауриц Корнелис Эшер.
Листы Мебиуса, или, как их еще называют, поверхности минимальной энергии, стали источником вдохновения для математических художников и скульпторов, например, Брента Коллинза или Макса Билла. Самый известный памятник ленте Мебиуса установлен у входа в вашингтонский Музей истории и техники.
Русские художники также не остались в стороне от этой темы и создали свои работы. Скульптуры «Лента Мебиуса» установлены в Москве и Екатеринбурге.
Литература и топология
Необычные свойства поверхностей Мебиуса вдохновили многих писателей на создание фантастических и сюрреалистических произведений. Петля Мебиуса играет важную роль в романе Р. Желязны «Двери в песке» и служит как средство перемещения сквозь пространство и время для главного героя романа «Некроскоп» Б. Ламли.
Фигурирует она и в рассказах «Стена темноты» Артура Кларка, «На ленте Мебиуса» М. Клифтона и «Лист Мебиус» А. Дж. Дейча. По мотивам последнего режиссером Густаво Москера был снята фантастическая кинокартина «Мебиус».
Делаем сами, своими руками!
Если вас заинтересовала лента Мебиуса, как сделать ее модель, вам подскажет небольшая инструкция:
1. Для изготовления ее модели потребуются:
— лист обычной бумаги;
2. Отрезаем полосу от листа бумаги так, чтобы ее ширина была в 5-6 раз меньше длины.
3. Полученную бумажную полоску раскладываем на ровной поверхности. Один конец придерживаем рукой, а другой поворачиваем на 1800 так, чтобы полоса перекрутилась и изнанка стала лицевой стороной.
4. Склеиваем концы перекрученной полосы так, как показано на рисунке.
Лента Мебиуса готова.
5. Возьмите ручку или маркер и посередине ленты начните рисовать дорожку. Если вы сделали все правильно, то вернетесь в ту же точку, откуда начали чертить линию.
Как много дел считались невозможными, пока они не были осуществлены!
Наука — это организованное знание.
Большинство читателей знают, что такое «кольцо Мебиуса», или хотя бы слышали о нем. Это кольцо интересно тем, что при разрезании вдоль распадается на более узкие кольца с совершенно неожиданными свойствами: либо с длиной окружности вдвое большей, чем у исходного, либо в виде двух продетых друг в друга колец. Придумали эту парадоксальную фигуру полтора века назад немецкие математики Август Фердинанд Мебиус (Möbius, 1790–1868) и Иоганн Бенедикт Листинг (Listing, 1808–1882).
Предложенная ими фигура, получившая впоследствии название «лист Мебиуса» (его называют также «лента» и «кольцо» Мебиуса), до сих пор остается одним из объектов изучения в области математики, называющейся «топология».
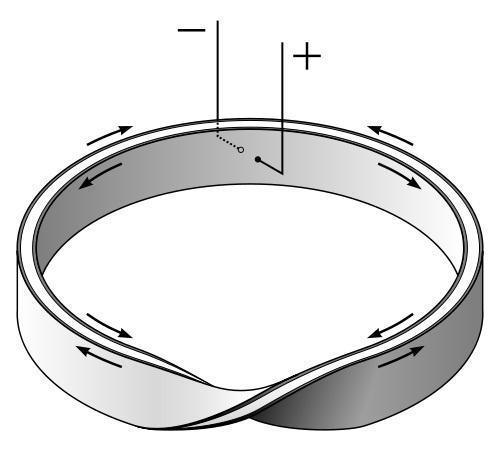
Чтобы изготовить такую фигуру, достаточно взять длинный узкий лист бумаги, так называемую «базовую ленту», закрутить спиралью на половину оборота, свернуть кольцом и склеить концы. Получится фигура в форме кольца, которую и называют «кольцом Мебиуса».
Если закрашивать обычный лист бумаги, то его можно окрасить в два цвета — каждую из поверхностей в свой цвет. Границей окрашивания будут края листа. С кольцом Мебиуса, склеенным из такого же листа, это не получится. При попытке окрасить одну его поверхность, он оказывается закрашенным полностью.
Прежде чем продолжить рассказ о кольце Мебиуса, определимся с терминами, используемыми в предлагаемой статье.
«Поверхность» — это часть обычного листа, или «базовой ленты», или кольца, отделенная от других ее частей краями. То есть у обычного листа всегда имеются две поверхности, разграниченные краями. Нельзя перейти с одной поверхности на другую, не пересекая при этом край.
«Сторона» — это часть поверхности листа, ленты или кольца, из одной точки которой можно перейти в любую другую ее точку, не пересекая край. Проще говоря, можно провести непрерывную черту от любой одной точки стороны до любой другой точки стороны и не пересечь при этом край.
Таким образом, у обычного листа или у плоской ленты количество поверхностей равно количеству их сторон, т. е. двум.
А вот у кольца Мебиуса (КМ) это не так. Ведь количество поверхностей у «базовой ленты», из которой изготовили кольцо, равнялось двум, и при изготовлении из нее КМ они никуда не делись. То есть у КМ две поверхности. Но при попытке окрасить одну из поверхностей КМ, оно оказывается закрашенным полностью. То есть у него есть только одна сторона. Это один из парадоксов КМ, плохо укладывающийся в обычную человеческую логику.
Если разрезать КМ на две равные по ширине части, то получается одно кольцо с длиной окружности, которая в два раза больше, чем у КМ. Оно имеет две стороны.
Если же КМ разрезать по линии, отступающей на одну треть от края, то оно распадается на два продетых друг в друга кольца разного размера. Одно — одностороннее, такого же размера, как КМ. Второе — двустороннее и в два раза длиннее, чем КМ.
До последнего времени считалось, что КМ уникально по своим свойствам, а односторонних фигур в форме колец, имеющих более двух поверхностей, не существует. Но оказалось, что это не так.
Чтобы убедиться в этом, нужно просто выйти за пределы привычного для нас стереотипного представления об односторонних фигурах. В данном случае было нужно придумать, изготовить и изучить свойства материальных моделей односторонних фигур с количеством поверхностей более двух. Такая работа была выполнена, и ее результаты представлены ниже.
Автор обращает ваше внимание на то, что речь, в данной статье, идет именно о материальных моделях фигур, а не об абстрактных математических фигурах. Хотя естественно, что показатели и свойства этих материальных фигур не противоречат законам математики. Материальные модели, в отличие от математических, понятны и доступны любому человеку. Их может легко изготовить неспециалист в математике и убедиться в правильности и воспроизводимости алгоритмов, приведенных в конце статьи.
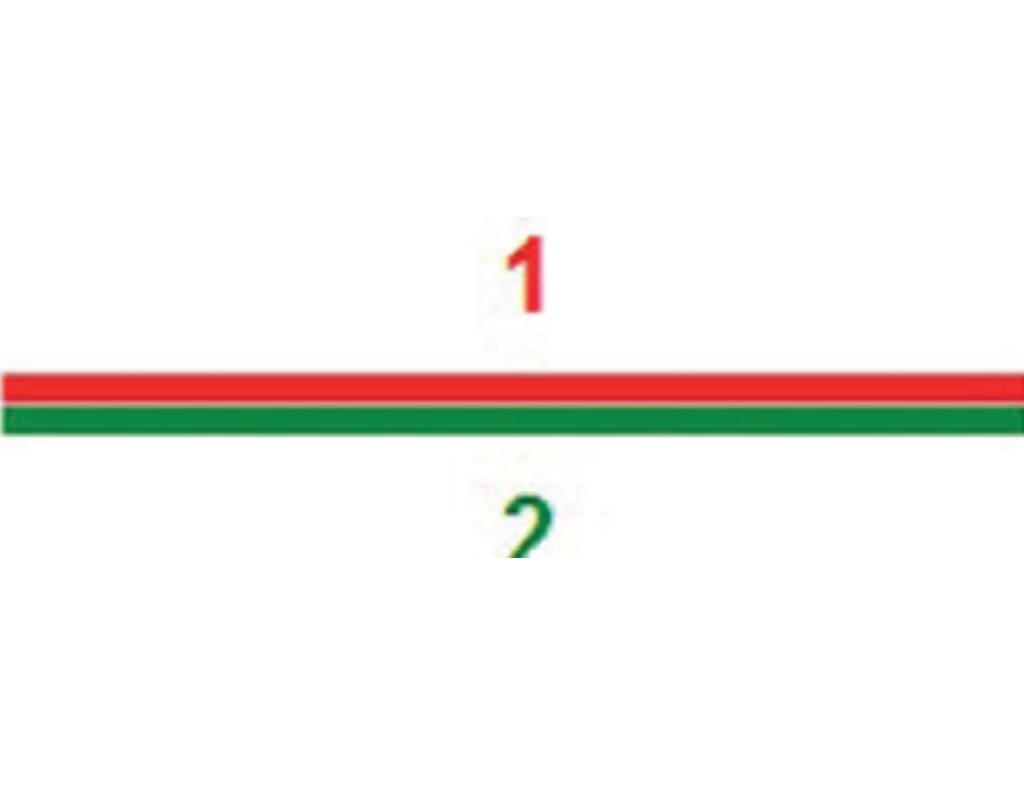
Первый вопрос, который возникает при изготовлении односторонних материальных моделей, имеющих более двух поверхностей: каким образом у базовой ленты может быть больше двух поверхностей? Действительно, если взять обычный лист бумаги, то он имеет две поверхности, разделенные границей — краями листа. Мы можем окрасить каждую из поверхностей в свой цвет. Поперечное сечение плоского листа выглядит как линия, рис. 1.
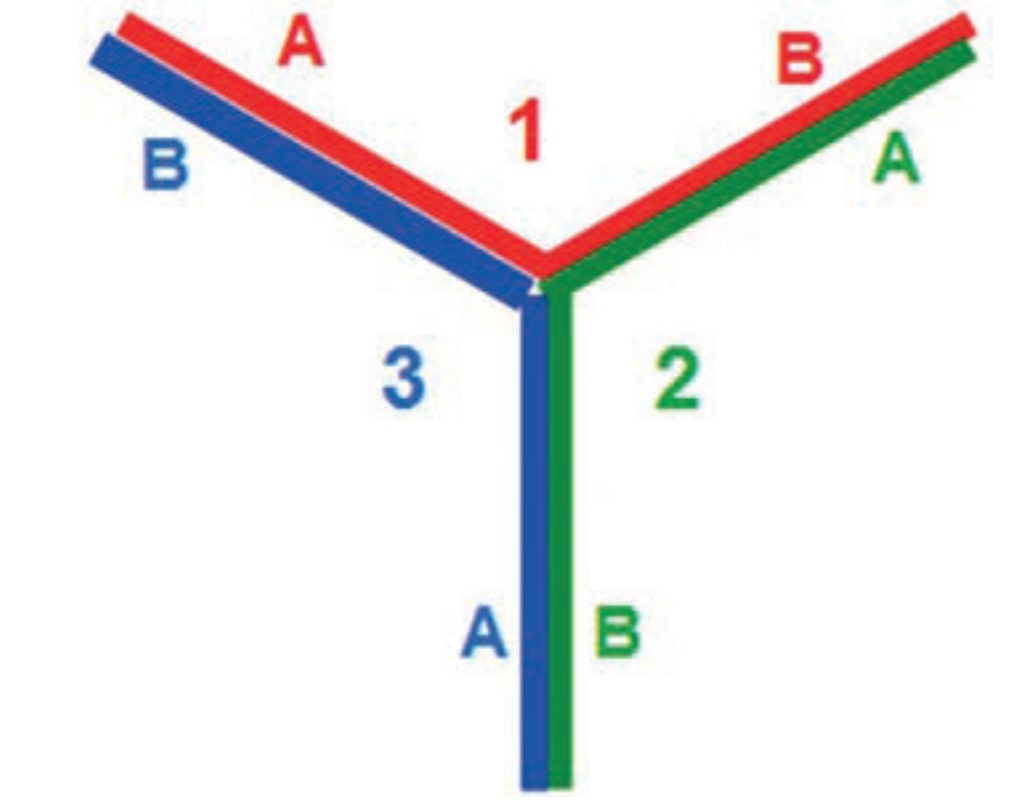
Теперь представим себе, что базовая лента не плоская, а имеет в сечении вид буквы Y. В этом случае, как видно на рис. 2, у ленты будет три поверхности, разграниченные краями. Каждая из поверхностей представляет собой ленту, согнутую вдоль под углом 120°.
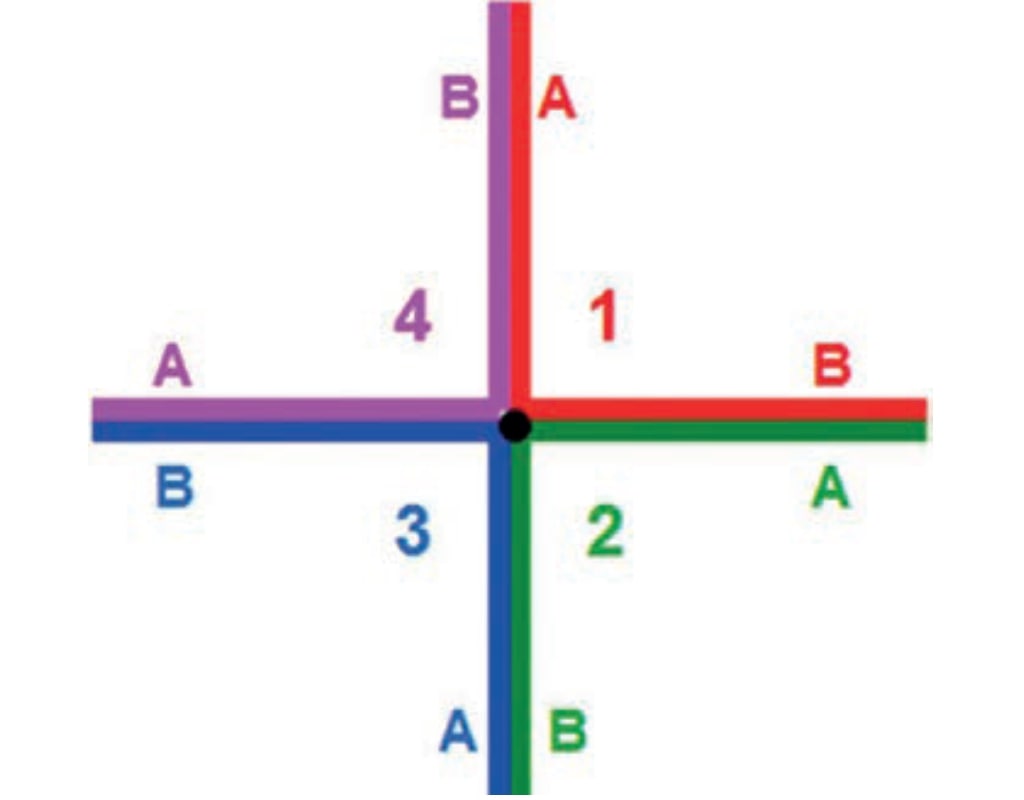
А чтобы базовая лента имела четыре поверхности, она должна иметь в сечении форму буквы Х, рис. 3.
Посмотрев на рис. 2 и 3, легко представить себе, как будут выглядеть сечения базовых лент с пятью, шестью и более поверхностями.
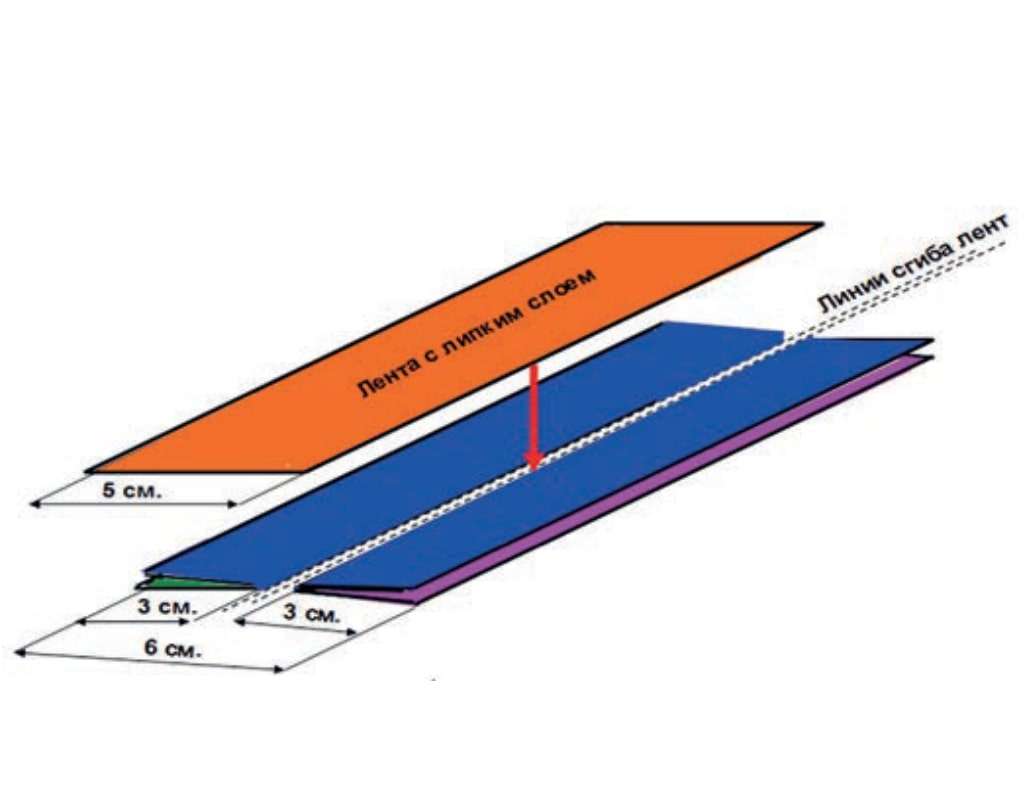
В качестве примера приводим описание процесса изготовления в материале базовой ленты с четырьмя поверхностями. Для этого понадобятся: лист бумаги длиной 70–80 см, ножницы, фломастер или шариковая ручка и клей для бумаги. Еще удобнее работать, если вместо клея использовать бумажную, так называемую малярную, ленту шириной около 5 см. Такую ленту с уже нанесенным на одну ее сторону липким слоем продают в виде рулонов в магазинах хозтоваров, в отделе лакокрасочных материалов.
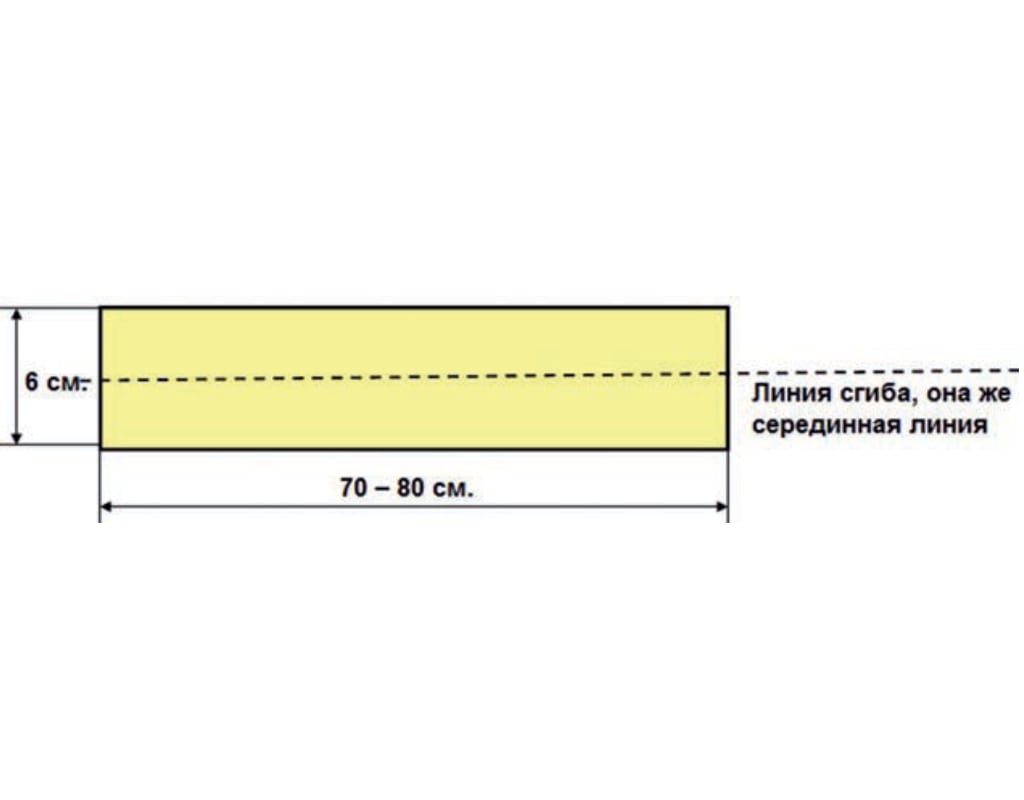
Бумагу нарезаем лентами шириной по 6 см. Затем берем две ленты и складываем каждую из них вдвое по линии сгиба (рис. 4).
Две сложенные вдоль ленты шириной по 3 см каждая прикладываем друг к другу линиями сгиба и склеиваем между собой по всей длине липкой малярной лентой (рис. 5).
Затем переворачиваем полученную «конструкцию» и укрепляем ее, наклеив малярную ленту на место соединения сложенных лент с другой стороны. Получается базовая лента с четырьмя поверхностями. Остается расправить ленту и убедиться, что в поперечном сечении она имеет вид креста, или «звезды» с четырьмя лучами (см. рис. 3).
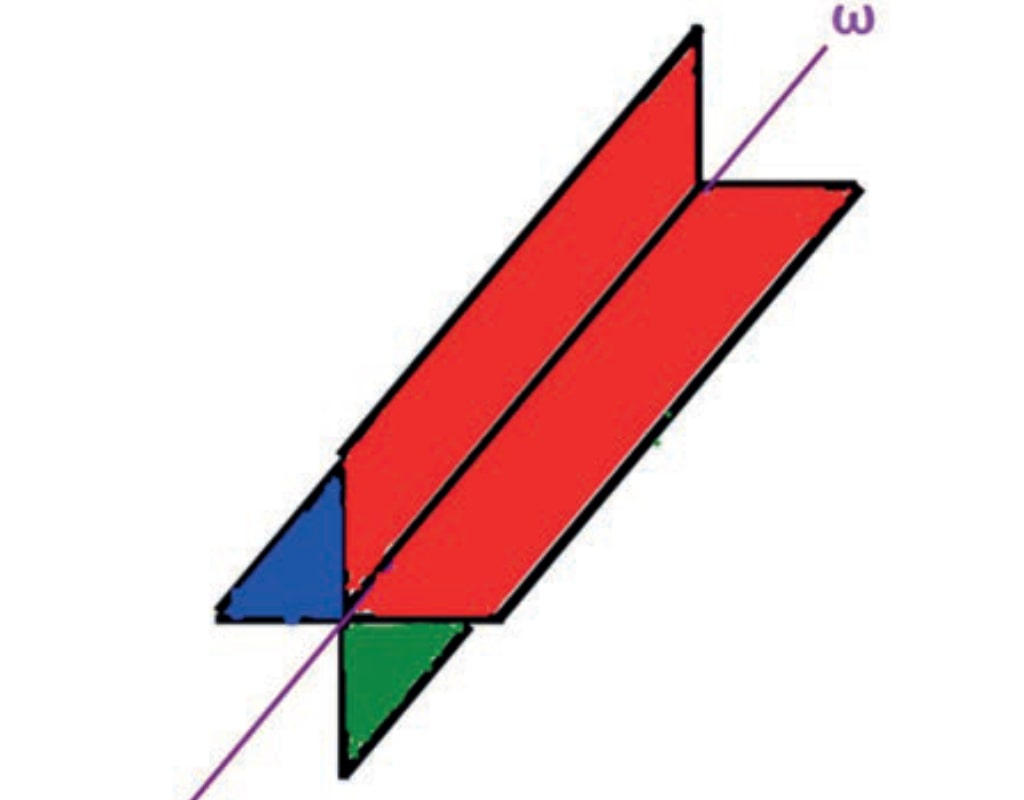
Для наглядности фрагмент базовой ленты Х с четырьмя поверхностями приведен на рис. 6 в аксонометрии. На рисунке видно, что каждая из поверхностей базовых лент представляет собой длинную узкую полосу, согнутую вдоль по серединой линии ω—ω.
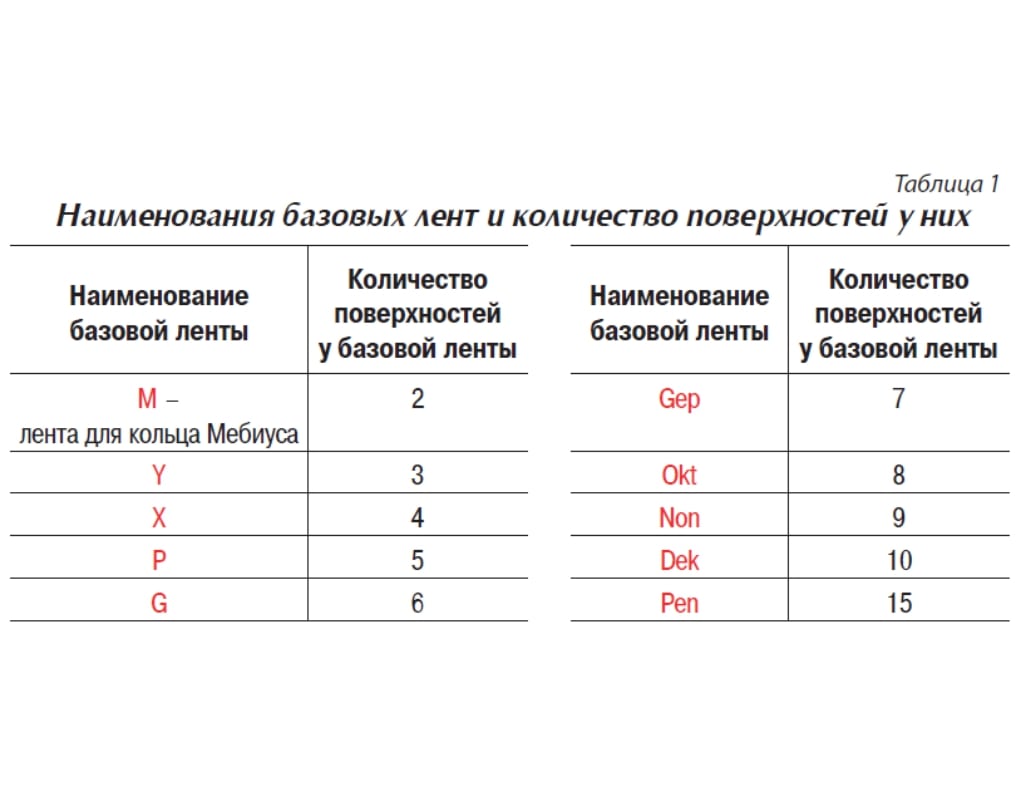
Для проведения исследований были изготовлены и изучены кольца из базовых лент, имеющих от двух до 15 поверхностей (табл. 1).
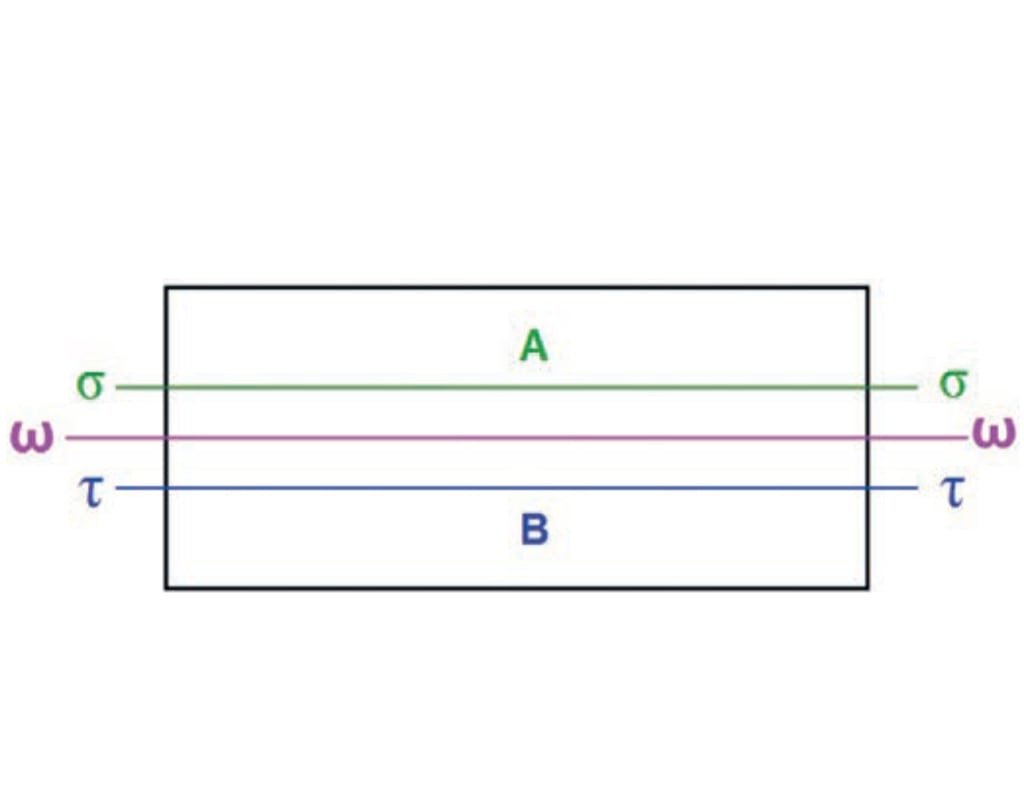
При проведении экспериментов и обсуждении их результатов в качестве эталона сравнения использовали, естественно, кольцо Мебиуса. Поэтому и на базовой ленте с двумя поверхностями (для изготовления кольца Мебиуса), и на базовых лентах с тремя, четырьмя и более поверхностями делали одинаковую разметку, схема которой приведена на рис. 7.
В статье использованы следующие условные термины, обозначения и сокращения:
Исходная фигура — фигура в форме кольца, полученного соединением концов базовой ленты.
Автор считает целесообразным кольца, получаемые непосредственно из базовых лент путем соединения их концов, называть исходными фигурами. Это позволяет при обсуждении результатов экспериментов не путать их с теми кольцами, на которые разделяются исходные фигуры после их разрезания по линиям ω—ω, τ—τ и σ—σ.
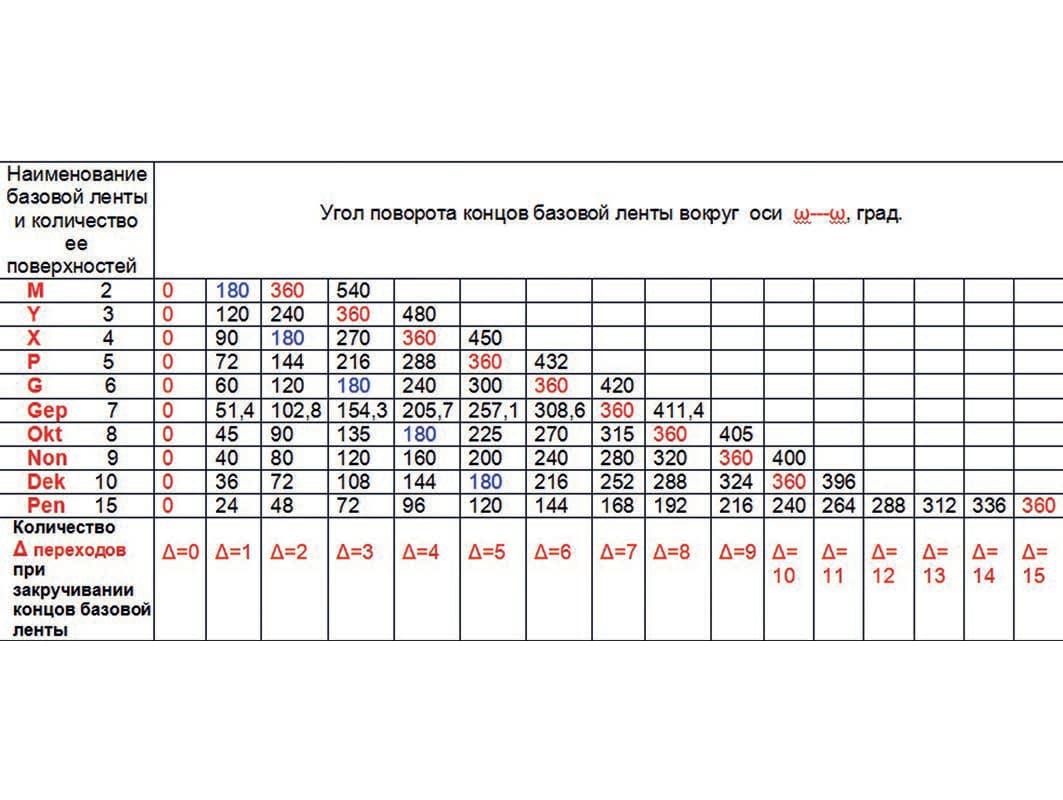
Угловой сектор — средняя величина угла между лучами на поперечном сечении базовой ленты. Например, у ленты с тремя поверхностями угловой сектор равен 360° : 3 = 120°, а у ленты с пятью поверхностями 360° : 5 = 72°.
Δ переход — количество угловых секторов, на которое сдвигаются концы базовых лент относительно друг друга при закручивании базовой ленты спиралью вокруг оси ω—ω перед склеиванием ее концов.
Npb — количество поверхностей у базовой ленты.
Np — количество поверхностей у исходных фигур и у колец. У исходных фигур Np = Npb; У колец, образующихся после разрезания исходной фигуры, количество поверхностей (Np) может быть самым разным, поэтому при изучении параметров колец их нужно каждый раз считать.
Ns — количество сторон у исходных фигур и у колец.
Nk — количество краев у исходных фигур и у колец.
Lo — длина окружности исходной фигуры. Она используется в качестве эталона сравнения и поэтому всегда условно принимается равной единице.
Lω — длина непрерывной черты, проведенной по линии ω—ω.
Lτ — длина непрерывной черты, проведенной по линии τ—τ.
Lσ — длина непрерывной черты, проведенной по линии σ—σ.
Nkol ω — количество колец, образующихся при разрезании исходной фигуры по линии ω—ω.
Nkol τσ — количество колец, образующихся при разрезании исходной фигуры по линии τ—τ или по линии σ—σ.
NL ω — количество непрерывных, не пересекающихся между собой черт, которые можно провести по линии ω—ω.
Np ω — количество поверхностей, через которые можно провести непрерывную черту по линии ω—ω.
NL τσ — количество непрерывных, не пересекающихся между собой черт, которые можно провести по поверхности исходной фигуры, по линии τ—τ или по линии σ—σ.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Концы базовых лент закручивали спиралью вокруг оси ω—ω на заданный угол (т. е. на заданное число градусов или на соответствующее им количество Δ переходов) относительно друг друга (табл. 2). Затем закрученные спиралью базовые ленты сворачивали кольцом и склеивали их концы. Получали трехмерные фигуры в форме колец, называемые в статье исходными фигурами.
Условные обозначения исходных фигур при их обсуждении составлены из наименования их базовой ленты ( Y, X, P, Okt, Dek и др., см. табл. 1) и угла закручивания базовых лент. Например, название исходной фигуры Dek-252 означает, что она получена из базовой ленты с 10 поверхностями, закрученной на 252° (т. е. на семь Δ переходов).
Внешний вид одной из изученных в работе исходных фигур (фигура Х-270) и ее поперечный разрез приведены в качестве примера на рис. 8 и 9.
Полученные исходные фигуры изучали. Сначала по их поверхностям проводили непрерывные черты по линиям ω—ω, τ—τ и σ—σ (см. рис. 7) и подсчитывали, сколько таких непрерывных и не пересекающихся между собой черт можно провести по поверхности каждой из исходных фигур. Затем исходные фигуры разрезали по этим же линиям и считали, на сколько колец они разделялись. Сравнивали длины окружностей полученных колец с длиной окружности их исходных фигур (Lo).
Подсчитывали число сторон (Ns) и краев (Nk) у каждого из полученных колец.
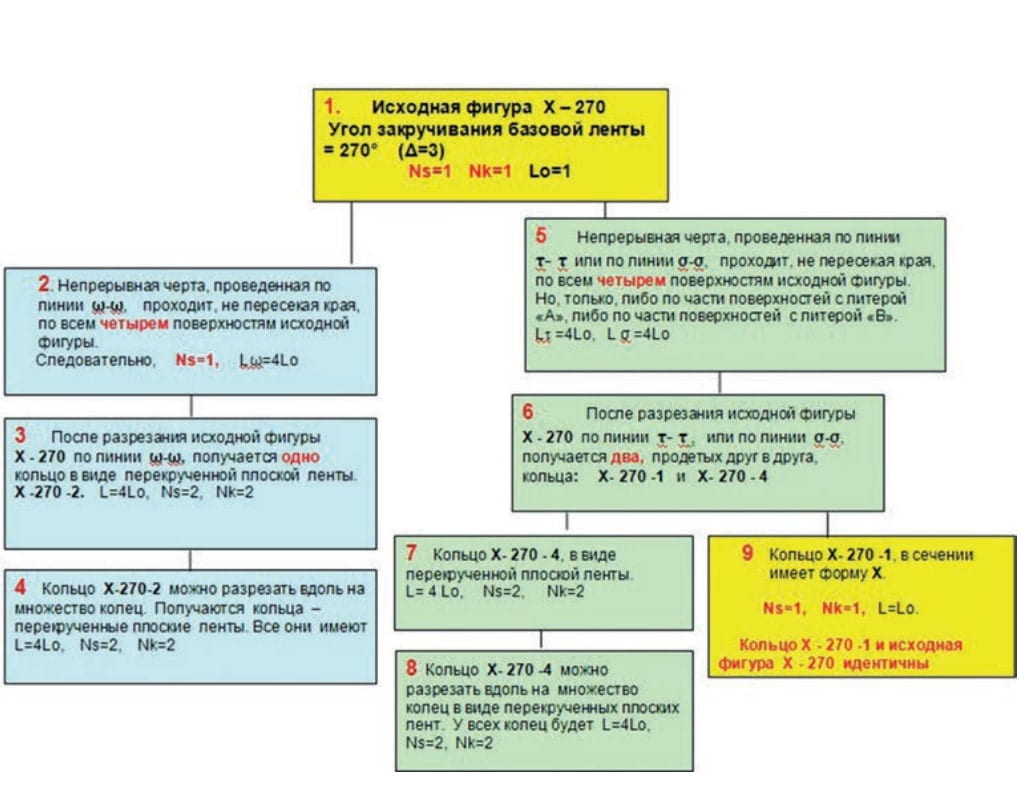
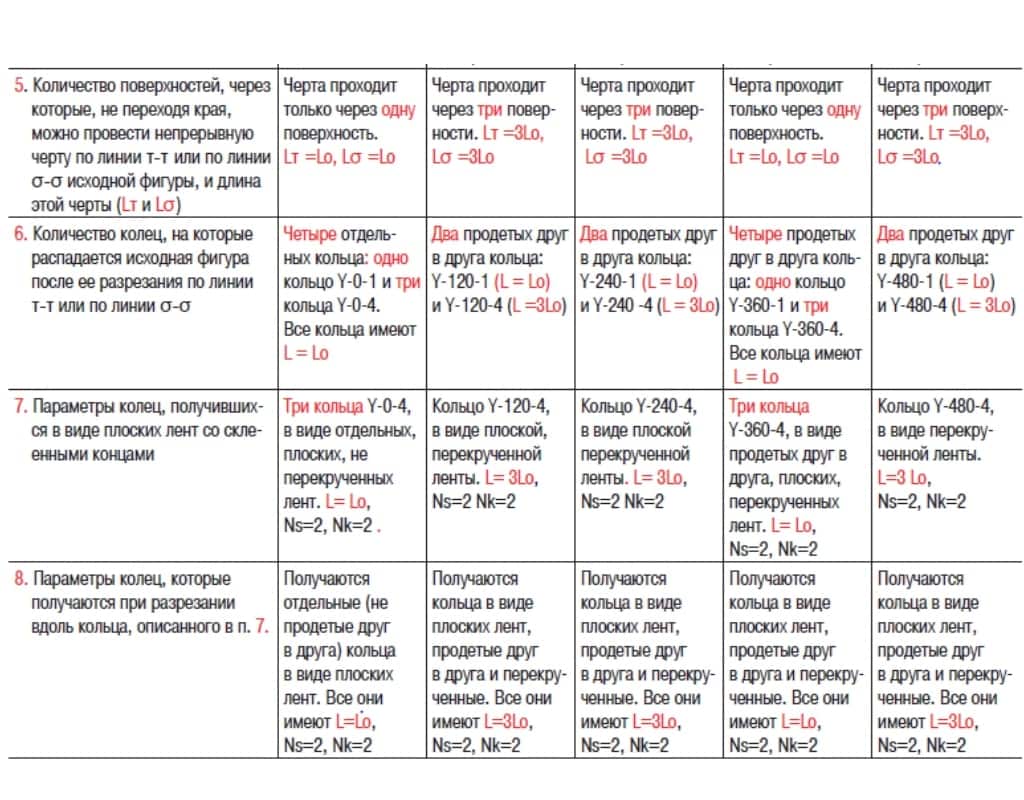
Полученные результаты оформляли в виде диаграмм. В качестве примеров такого оформления результатов, приведены диаграммы для колец из базовой ленты X с четырьмя поверхностями при угле закручивания ленты 270 °(исходная фигура Х-270, рис. 10) и из базовой ленты G с шестью поверхностями при угле закручивания ленты 120°(исходная фигура G-120, рис. 11).
На рис. 10 видно, что при угле закручивания базовой ленты Х на 270° получаемая из нее исходная фигура (на диаграмме она обозначена желтым прямоугольником 1) имеет одну сторону (Ns = 1). Это следует из того, что непрерывная черта, проведенная по ней (голубой прямоугольник 2), проходит через все четыре поверхности базовой ленты Х. То есть из любой точки поверхности исходной фигуры Х-270 мы можем попасть в любую другую ее точку. Следовательно, исходная фигура Х-270 имеет только одну сторону.
При разрезании фигуры Х-270 по линии ω—ω она превращается в одно двустороннее кольцо с длиной окружности в 4 раза больше, чем у исходной фигуры (голубой прямоугольник 3). Последующие разрезания вдоль кольца Х-270-2 (голубой прямоугольник 4) не меняют его показателей.
При разрезании исходной фигуры Х-270 по линиям τ—τ или σ—σ (зеленый прямоугольник 6) она разделяется на два продетых друг в друга кольца. Одно из этих колец идентично исходной фигуре (желтый прямоугольник 9), а другое имеет две стороны и длину окружности в 4 раза больше, чем у исходной фигуры (зеленый прямоугольник 7).
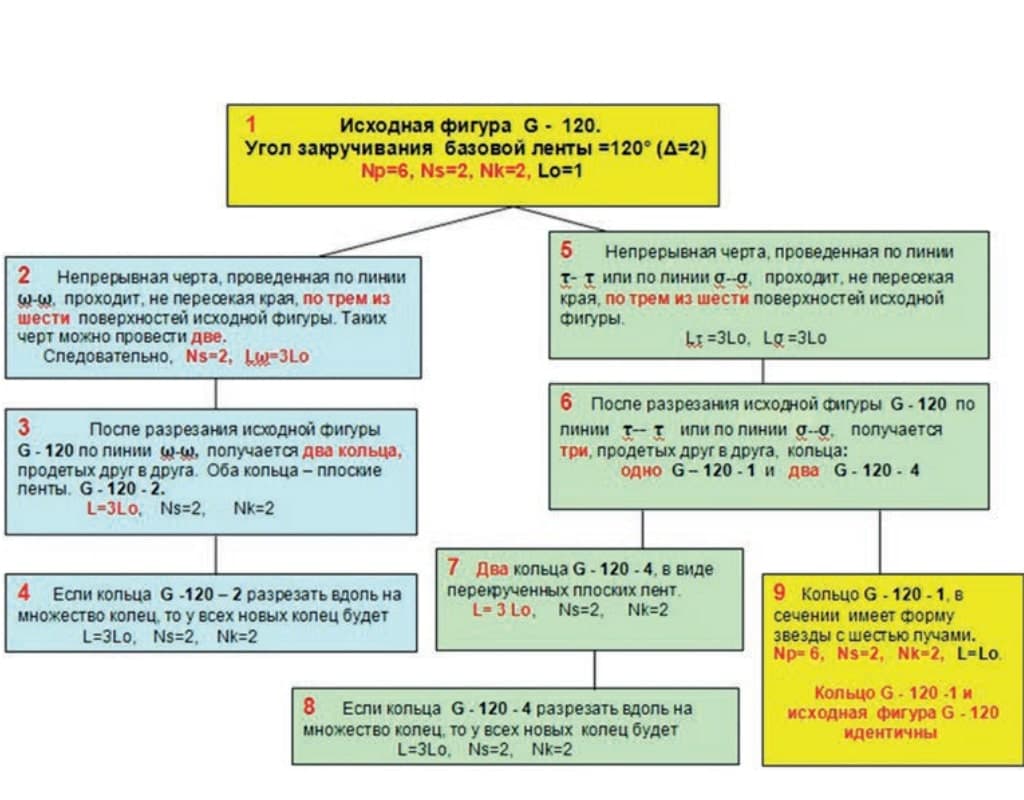
Аналогичное исследование проведено для исходной фигуры G-120 (рис. 11), полученной из базовой ленты G, при закручивании её на 120°. Установлено, что по поверхности этой фигуры можно провести две непрерывные, не пересекающиеся между собой черты. Каждая их этих черт проходит через три из шести поверхностей базовой ленты G (голубой прямоугольник 2). Следовательно, исходная фигура G-120 имеет 2 стороны (желтый прямоугольник 1).
При разрезании фигуры G-120 по линии ω—ω, она распадается на два продетых друг в друга плоских перекрученных кольца, каждое из которых имеет длину окружности в три раза больше, чем окружность исходной фигуры G-120 (голубой прямоугольник 3).
При разрезании исходной фигуры G-120 по линиям τ—τ или σ—σ (зеленый прямоугольник 6) она распадается на три продетых друг в друга кольца, одно из которых идентично исходной фигуре (желтый прямоугольник 9), а два других имеют по две стороны и длины окружностей в 3 раза больше, чем у исходной фигуры (зеленый прямоугольник 7).
На рис. 10 и 11 приведены диаграммы результатов изучения показателей только двух исходных фигур и колец из них. Это сделано в качестве примера первичной обработки результатов исследований. На самом деле при выполнении работы было изготовлено и изучено более 90 исходных фигур, указанных в табл. 2, а также все кольца, полученные при их разрезании.
Для уменьшения объема описания экспериментальной части работы остальные диаграммы в ней не приведены, а сразу приведены таблицы и графики, сделанные по результатам обработки диаграмм.
На основе таблиц построены графики, приведенные на рис. 12–15. На этих графиках сведены вместе основные показатели исходных фигур всех изученных серий. Параметры исходных фигур на этих графиках приведены в виде их зависимостей от величины углов закручивания базовых лент. А поскольку ось абсцисс на всех графиках проградуирована в одинаковых единицах, это позволяет удобно сравнивать полученные результаты между собой.
Однако фактически параметры материальных исходных фигур зависят не от абсолютной величины углов закручивания их базовых лент, а от количества Δ переходов, на которое концы лент повернуты относительно друг друга перед их склеиванием. Но, с другой стороны, выяснилось, что если ось абсцисс на рисунках размечать только в Δ переходах, то сравнивать на графиках и обсуждать результаты экспериментов, проведенных с исходными фигурами разных серий, становится неудобно. Это обусловлено тем, что при одинаковых углах закручивания базовых лент с разным числом поверхностей количество Δ переходов может отличаться в разы. Поэтому сравниваемые графики придется рисовать в разных масштабах, а это ставит под сомнение саму правомерность их сравнения. Это хорошо видно, например, на рис. 15.
Чтобы устранить данное противоречие, на некоторых графиках (там, где это было необходимо) градуировка оси абсцисс наряду с углами закручивания ленты продублирована еще и количеством Δ переходов. Это позволяет сравнивать и обсуждать результаты экспериментов более корректно и углубленно, чем если бы была использована ось абсцисс, размеченная только в градусах. Использование «двойной» разметке оси абсцисс дает возможность использовать при обсуждении две точки отсчета, что позволяет лучше понять сущность полученных результатов. В последующем полученные в результате экспериментов данные были использованы для разработки алгоритмов, позволяющих «предсказать» показатели исходных фигур и колец, образующихся при их разрезании, не изготавливая их материальных моделей.
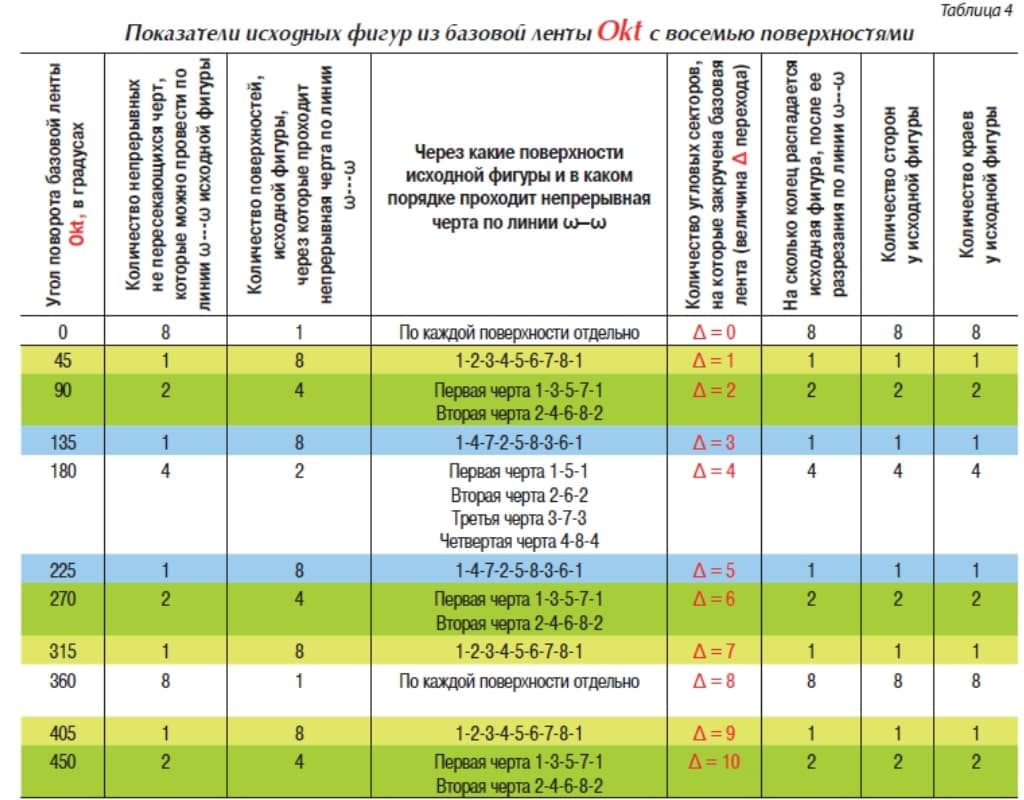
Целесообразность рассмотрения полученных в работе результатов с двух точек зрения хорошо видна в табл. 4 для исходных фигур серии Okt. В столбце 4 этой таблицы показан порядок перехода непрерывной черты, проведенной по линии ω—ω, с одной поверхности на другую в зависимости от количества Δ переходов, на которые были повернуты концы базовой ленты при ее закручивании спиралью (столбец 5).
В столбце 4 табл. 4 видно, что эта черта проходит по поверхностям в определенном порядке. Осью симметрии является отметка 180° (Δ = 4). По равноудаленным от нее исходным фигурам (в таблице их параметры окрашены в одинаковые цвета) непрерывная черта по серединной линии ω—ω переходит с одной поверхности исходной фигуры на другую поверхность в той же последовательности, что и по симметрично им расположенным исходным фигурам, находящимся по другую сторону отметки 180° (Δ = 4). Термин «равноудаленным» означает в данном случае то, что исходные фигуры удалены от отметки 180° на одинаковое количество Δ переходов. В серии Okt равноудаленными являются исходные фигуры с Δ = 3 и Δ = 5, с Δ = 2 и Δ = 6, с Δ = 1 и Δ = 7, с Δ = 0 и Δ = 8.
Аналогичные эксперименты были проделаны и с другими изученными сериями исходных фигур. Во всех случаях симметричность (относительно отметки 180°) порядка прохождения непрерывной черты по линии ω—-ω исходных фигур подтвердилась.
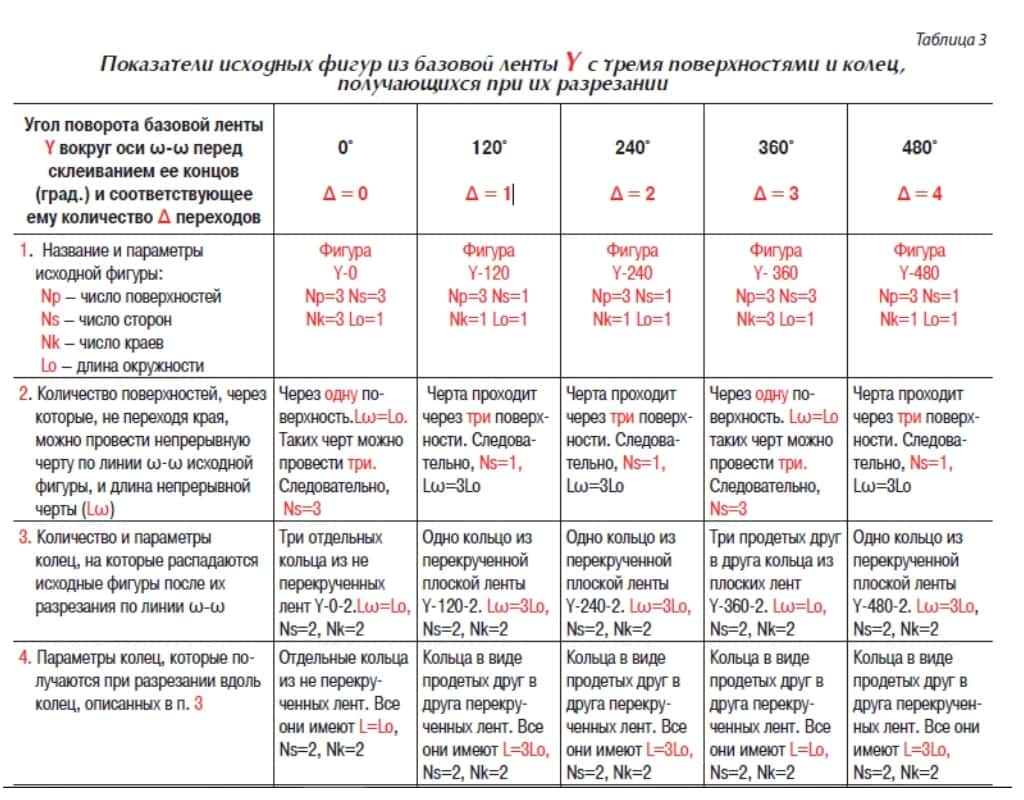
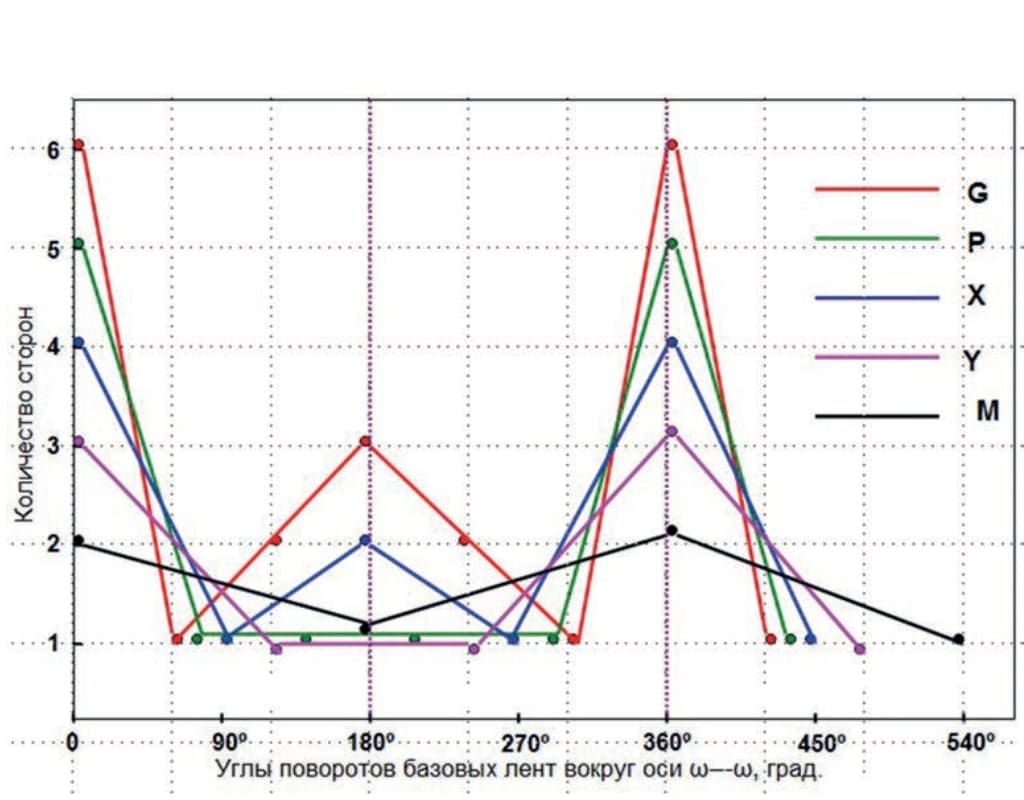
На рис. 12 приведены графики зависимости количества сторон у исходных фигур, изготовленных из базовых лент, имеющих от двух до шести поверхностей, от углов закручивания лент. Кривая Y на нем соответствует данным табл. 3.
На рис. 12 видно, что в пределах одного оборота базовой ленты вокруг оси ω—ω от 0° до 360° исходные фигуры имеют следующие показатели:
На графиках, приведенных на рис. 12, видно, что прямой зависимости между количеством поверхностей у базовых лент и числом сторон у получаемых из них исходных фигур нет.
Общим для всех рассмотренных случаев является то, что если склеивать концы базовых лент, не закручивая их предварительно спиралью вокруг оси ω—ω, т. е. при угле закручивания 0°, и после закручивания на полный оборот, т. е. на 360°, всегда получаются исходные фигуры, у которых количество сторон (Ns) равно числу поверхностей (Npb) их базовых лент.
На рис. 12 видно также, что при углах закручивания базовых лент, ближайших к 0° и к 360°, из них всегда получаются односторонние исходные фигуры, независимо от того, сколько поверхностей было у их базовых лент.
Результаты, приведенные на рис. 12, показывают, что какие-то зависимости в ряду исходных фигур в форме колец с разным количеством поверхностей явно имеются.
Напоминаем Вам, что в нашем журнале «Наука и техника» Вы найдете много интересных оригинальных статей о развитии авиации, кораблестроения, бронетехники, средств связи, космонавтики, точных, естественных и социальных наук. На сайте Вы можете приобрести электронную версию журнала за символические 60 р/15 грн.
В нашем интернет-магазине Вы найдете также книги, постеры, магниты, календари с авиацией, кораблями, танками.









 masterok
masterok