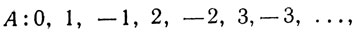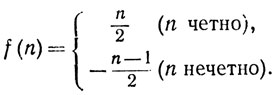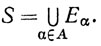конечное и счетное множество в чем разница
Конечное и бесконечное в математике. Лекция Павла Кожевникова для старшеклассников в Яндексе
В отличие от окружающего нас мира, в котором всё конечно, в математике мы часто сталкиваемся с бесконечными объектами. Например, бесконечны множества целых, рациональных, алгебраических, конструктивных или действительных чисел. На лекции мы рассмотрим задачи, в которых проявляются некоторые принципы работы с бесконечными множествами. Иногда эти принципы сильно отличаются от тех, к которым мы привыкли в случае «конечного» мира.
Гильбертов отель
Представим себе гипотетический отель с бесконечным количеством номеров. Все номера в отеле уже заселены. но в определенный момент в отель приезжает еще один постоялец. Несмотря на то, что в каждом номере отеля уже есть хотя бы один жилец, комнату для нового все же можно найти. Ведь наш отель бесконечен, и если попросить всех постояльцев переселиться на один номер дальше, самый первый номер окажется свободен. И даже если приедет несколько новых постояльцев, путем серии подобных переселений, можно будет найти место и для них.
А теперь представим, что у нас три таких гильберотовых отеля. Два из них закрываются на ремонт, и постояльцев нужно расселить в один оставшийся. Даже такой необычный случай не должен вызвать никаких проблем, всем постояльцам найдется место в третьем бесконечном отеле. Например, мы можем последовательно расселять постояльцев из двух отелей по четным и нечетным номерам соответственно.
Представим еще более странную ситуацию: бесконечное количество гильбертовых отелей закрывается на ремонт, и нам нужно расселить всех их постояльцев в один бесконечный отель. Если мы воспользуемся приемом из предыдущего примера, но будем расселять постояльцев последовательно по диагонали, рано или поздно нам удастся распределить всех.
Попробуем формализовать рассмотренные нами только что задачи с точки зрения теории множеств. Что мы по сути сейчас делали? Мы нумеровали комнаты отеля. Такая ситуация в математике называется счетным множеством: бесконечное множество K, которое можено перенумеровать. Бесконечное множество называется счетным, если существует взаимно однозначное соответствие между элементами множества K и натуральными числами <1, 2, …>. Формальное представление рассмотренных нами задач выглядит следующим образом:
Счетные и несчетные множества
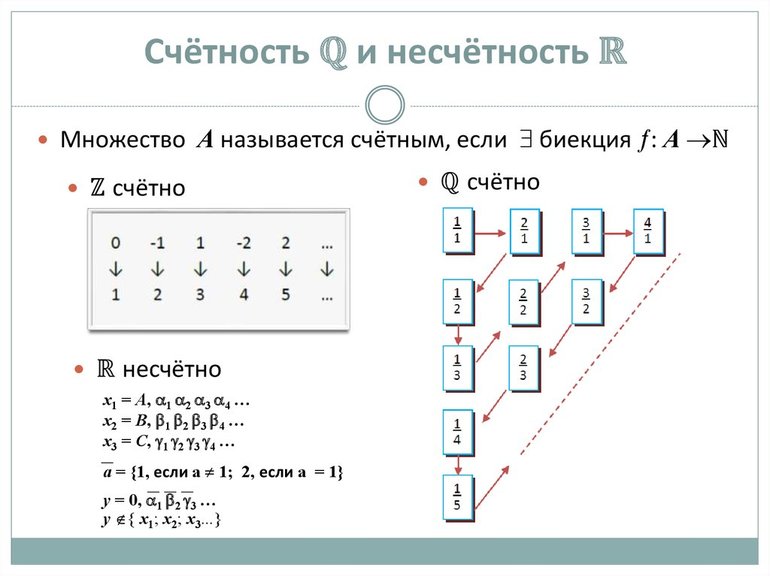
Но перейдем к более привычным для нас множествам – числовым. И начнем с натуральных чисел. Очевидно, что множество натуральных чисел (ℕ) счетное просто по определению. Если мы добавим к натуральным числам ноль и отрицательные числа, мы получим множество целых чисел. Счетное ли это множество? Мы уже говорили выше, что если объединить два счетных множества, результат также будет счетным множеством. От добавления 0 множество не потеряет свойства быть счетным.
Далее рассмотрим рациональные числа. Это множество чисел, представимых в виде m/n, где m – целое число, а n – натуральное:
Таким образом, рациональные числа представляют собой счетное число счетных множеств и при объединении также станут счетным множеством.
Алгебраические числа – это множество корней многочленов с целыми коэффициентами. Будет ли это множество счетным? Множества корней многочленов разных степеней являются счетными множествами, а значит, результат их объединения также будет счетным множеством. Из этого следует, что множество алгебраических чисел (𝔸) – это счетное множество.
Существуют так называемые трансцендентные числа: в это множество (𝕀) входят действительные (ℝ), но не алгебраические (𝔸) числа. К этому множеству относятся числа e, π и т.д.
Раз уж мы упомянули действительные числа, остановимся на них подробнее, тем более, что как раз их множество счетным не является, что мы сейчас и докажем. И для этого нужно доказать что множество бесконечных десятичных дробей несчетно. Для простоты представим, что после запятой у нас могут быть только нули и единицы:
Допустим, что у нас есть бесконечная таблица, в которой пронумерованы все числа, указанного нами вида.
| 0,a1, a2, a3, a4, a5 … |
| 0,b1, b2, b3, b4, b5 … |
| 0,c1, c2, c3, c4, c5 … |
| 0,d1, d2, d3, d4, d5 … |
| . |
| . |
| . |
Докажем, что такой таблицы существовать не может, сконструируем такую дробь, встретить которую в этой таблице невозможно:
Где x1≠a1, x2≠b2, x3≠c3 и т.д. Называется это канторовым диагональным процессом, он приводит нас к числу, которого нет в нашей таблице. А значит, множество у нас несчетное.
Посмотрев лекцию до конца, вы узнаете какие бывают задачи, связанные с бесконечными множествами, и как они решаются.
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
Сравнение и отображение
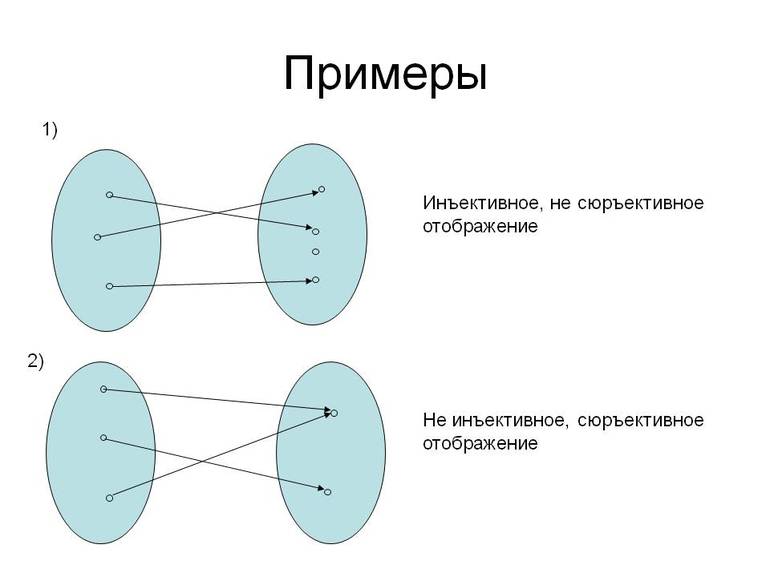
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
Счётные и несчётные множества — понятие, свойства и примеры
Множество — это совокупность или набор элементов. Количество этих элементов называется мощностью этой совокупности. Мощность пустого набора компонентов равна нулю. С размером конечных совокупностей тоже всё просто. У них можно пересчитать количество компонентов. А вот возможность посчитать компоненты бесконечности различает счётные и несчётные множества.
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
Сравнение и отображение
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Поскольку N отображается в R конъюнктивно (N является подмножеством R, но не имеет подмножества эквивалентного R), то |R|=c > a=|N|. А так как R представляет собой объединение совокупностей Q и I, то размер |I| = |R| — |Q| = c — a = c. Значит, I тоже континуально.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
Глава 2. Элементы теории множеств
Конечные, счетные и несчетные множества
Мы начнем этот раздел с определения понятия функции.
2.1. Определение. Рассмотрим два множества А и В, элементами которых могут быть любые объекты, и предположим, что каждому элементу х множества A некоторым способом поставлен в соответствие элемент множества В, который мы обозначим через f(х). Тогда f называется функцией из A в В (или отображением множества А в В).
Множество А называется областью определения функции f (мы будем говорить также, что f определена на A), а элементы f(х) называются значениями f. Множество всех значений функции f называется ее областью значений.
2.2. Определение. Мы будем говорить, что множество А есть подмножество множества В, и писать A⊂В (или В⊃A), если каждый элемент множества А является элементом множества В. Если, кроме того, в В имеется элемент, не принадлежащий А, то А называется собственным подмножеством множества В.
В частности, пустое множество ∅ служит подмножеством любого множества, и A⊂ A, каково бы ни было множество A.
Если А ⊂ В и В ⊂ A, то мы будем писать А = В.
2.3. Замечание. То обстоятельство, что пустое множество является подмножеством любого множества, связано с одной логической тонкостью, часто вызывающей трудности у начинающих.
Из определения 2.2 ясно, что если множество A не есть подмножество множества В, то должно быть верным следующее утверждение: «существует элемент х, такой, что х ∈А и х ∉В». Но если A пусто, то не существует такого х, что х ∈А, и высказанное только что утверждение ложно.
Подобные рассуждения применимы всегда, когда мы хотим проверить, что пустое множество удовлетворяет некоторым условиям.
2.5. Определение. Если существует взаимно однозначное отображение множества A на множество В, то мы будем говорить, что между A и В может быть установлено взаимно однозначное соответствие, или что A и В имеют одно и то же кардинальное число, или, короче, что A и В эквивалентны, и будем писать А
В. Это отношение, очевидно, обладает следующими свойствами:
симметричность: если А
транзитивность: если A
Всякое отношение, обладающее этими тремя свойствами, называется отношением эквивалентности.
(a) А конечно, если A
Jn при некотором n (пустое множество также считается конечным);
(b) А бесконечно, если A не является конечным;
(d) А несчетно, если A не конечно и не счетно;
(e) А не более чем счетно, если A или конечно, или счетно.
В тогда и только тогда, когда A и В содержат одно и то же число элементов. Однако для бесконечных множеств смысл слов «содержат одно и то же число элементов» становится очень туманным.
Он проясняется с помощью понятия взаимно однозначного соответствия.
В этом примере мы можем даже указать в явном виде формулу для отображения f множества J в A, устанавливающего взаимно однозначное соответствие между этими множествами:
В действительности мы могли бы заменить определение 2.6 (b) следующей формулировкой: A бесконечно, если A эквивалентно одному из своих собственных подмножеств.
Ввиду того что всякое счетное множество служит множеством значений некоторой взаимно однозначной функции, определенной на J, мы можем рассматривать всякое счетное множество как множество значений некоторой последовательности с различными членами. Допуская некоторую вольность речи, говорят, что элементы любого счетного множества можно «расположить в последовательность».
Иногда удобно заменить в этом определении J множеством всех неотрицательных целых чисел, т. е. начинать с 0, а не с 1.
2.10. Теорема.Всякое бесконечное подмножество счетного множества А счетно.
Доказательство. Предположим, что Е⊂A и E бесконечно. Расположим элементы х множества А в последовательность <хn> с различными членами. Построим последовательность
Эта теорема показывает, что, грубо говоря, счетные множества представляют «наименьшую» бесконечность: никакое несчетное множество не может быть подмножеством счетного.
Объединение семейства множеств <Еα> определяется как множество S, такое, что х*#8712;S тогда и только тогда, когда х∈Еα хотя бы при одном α∈A. Мы будем пользоваться обозначением