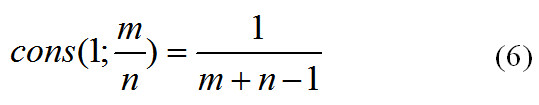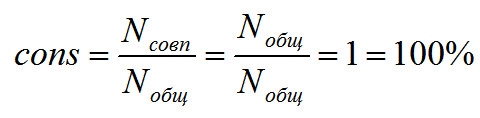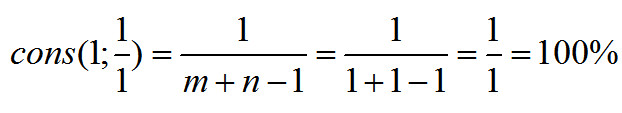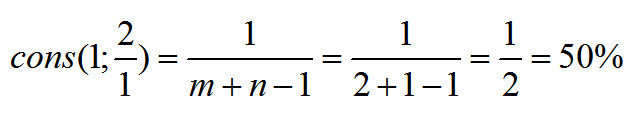консонанс что это в музыке
Консонанс (в музыке)
Лит.: Гельмгольц Г., Учение о слуховых ощущениях как физиологическая основа для теории музыки, пер. с нем., СПБ, 1875; Шевалье Л., История учений о гармонии, пер. с франц., М., 1931; Клещов С. В., К вопросу о различии диссонирующих и консонирующих созвучий, «Труды физиологических лабораторий им. акад. И. П. Павлова», т. 10, М.— Л., 1941; Чайковский П. И., Руководство к практическому изучению гармонии, Собр. соч., т. Ill а, М., 1957; Медушевский В. В., Консонанс и диссонанс как элементы музыкальной знаковой системы, в кн.: VI Всесоюзная акустическая конференция, М., 1968, секция К.; Stumpf К., Konsonanz und Dissonanz, Lpz., 1898 (Beiträge zur Akustik und Musikwissenschaft, H. 1).
Полезное
Смотреть что такое «Консонанс (в музыке)» в других словарях:
Консонанс и диссонанс — (фр. consonance, от лат. consonantia созвучие, согласное звучание, и фр. dissonance, от лат. dissonantia нестройность, нестройное звучание) противоположные понятия теории музыки, характеризующие слияние или… … Википедия
Консонанс — и диссонанс (фр. consonance, от лат. consonantia созвучие, согласное звучание, и фр. dissonance, от лат. dissonantia нестройность, нестройное звучание) противоположные понятия теории музыки, характеризующие слияние или неслияние в восприятии… … Википедия
консонанс — а, м. consonance f. 1. Муз. Сочетание 2 х или нескольких звуков, образующих согласованное, слитное звучание. К консонирующим интервалам по традиции относят чистую приму, кварту, квинту, октаву. Булучевский 1998. Созвучие, из которого формируется… … Исторический словарь галлицизмов русского языка
КОНСОНАНС — (французское consonance созвучие) в музыке, слитное, гармоничное одновременное звучание различных тонов. Противоположен диссонансу … Современная энциклопедия
КОНСОНАНС — (франц. consonance созвучие) 1) в музыке слитное, согласованное одновременное звучание различных тонов; один из важнейших элементов гармонии. Понятие консонанса противостоит понятию диссонанса. К консонансу относят приму, октаву, квинту, кварту,… … Большой Энциклопедический словарь
Консонанс — (consonanza) в музыке обозначает созвучие в приме(отношение чисел колебания одного и другого звука 1 : 1), октаве(отношение 1 : 2), дуодециме (1 : 3), чистой квинте (2 : 3), чистойкварте (3 : 4), большой сексте (3 : 5), большой терции (4 : 5),… … Энциклопедия Брокгауза и Ефрона
Консонанс — (французское consonance созвучие) в музыке, слитное, гармоничное одновременное звучание различных тонов. Противоположен диссонансу. … Иллюстрированный энциклопедический словарь
Консонанс — (франц. consonance, от лат. consonantia слитное, согласное звучание, созвучие, гармония) слияние в восприятии одновременно звучащих тонов, а также созвучие, воспринимаемое как слияние тонов. Понятие К. противоположно понятию диссонанса. К … Музыкальная энциклопедия
консонанс — а; м. [франц. consonance] 1. Муз. Гармоническое сочетание нескольких звуков; благозвучие (противоп.: диссонанс). 2. Лит. Рифма с различными ударными гласными, основанная на совпадении ряда послеударных, а иногда и предударных звуков. * * *… … Энциклопедический словарь
Консонанс — (consonanza) в музыке обозначает созвучие в приме (отношение чисел колебания одного и другого звука 1:1), октаве (отношение 1:2), дуодециме (1:3), чистой квинте (2:3), чистой кварте (3:4), большой сексте (3:5), большой терции (4:5), малой терции… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Значение слова «консонанс»
1. Муз. Гармоническое сочетание нескольких звуков; благозвучие; противоп. диссонанс.
2. Лит. Рифма с различными ударными гласными, основанная на совпадении ряда послеударных, а иногда и предударных звуков.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
КОНСОНА’НС, а, м. [от латин. consonantia] (муз.). Созвучие, согласное звучание нескольких звуков в аккорде; противоп. диссонанс.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
консона́нс
1. муз. гармоничное сочетание нескольких звуков; созвучие, благозвучие ◆ И там одна фальшивая нота портит стройный аккорд, убивает благозвучие, превращает консонанс в диссонанс и заставляет все остальные ноты звучать фальшиво. К. С. Станиславский, «Работа актера над собой», 1938 г. (цитата из НКРЯ) ◆ В любом курсе основ музыкальной акустики можно прочитать, что если отношение чисел колебаний двух тонов представляет собой отношение простых чисел от 1 до 6, это называется акустическим консонансом, в противном случае — акустическим диссонансом. С. А. Еремеева, «Лекции по русскому искусству», 2000 г. (цитата из НКРЯ)
2. лингв. вид рифмы, в которой ударные гласные различны, но послеударный ряд звуков, а иногда и предударные звуки совпадают ◆ Тут мы имеем дело с начальной стадией нашего виршевого искусства, ещё досиллабического, характеризовавшегося неравносложностью строк, отсутствием цезуры, глагольной в большинстве случаев рифмой, заменяемой иногда ассонансом или консонансом. Н. К. Гудзий, «История древней русской литературы. (XVI–XVII вв.)», 1938 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова дьюар (существительное):
Гармонические и мелодические интервалы в музыке
Интервал в музыке – это сочетание двух звуков. Но сочетаться они могут по-разному: их можно сыграть или спеть одновременно или по очереди.
Гармонический интервал – это такой интервал, звуки которого берутся единовременно. Такие интервалы являются основой музыкальной гармонии, именно поэтому они имеют такое название.
Мелодический интервал – это интервал, в котором звуки берутся вразбивку: сначала один, затем второй. Из названия понятно, что такие интервалы рождают мелодии. Ведь любая мелодия представляет собой цепочку, в которой соединены несколько одинаковых или разных интервалов.
Мелодические интервалы могут быть восходящими (шаг от нижнего звука к верхнему) и нисходящими (переход от верхнего звука к более низкому).
Как различать интервалы на слух?
Гармонические и мелодические интервалы нужно уметь различать на слух. На уроках сольфеджио в музыкальных школах и колледжах даже практикуются специальные упражнения на слуховой анализ, когда учащимся играются разные созвучия, а они «отгадывают» что именно им сыграли. Но как это сделать?
Есть много разных способов, которые помогают запоминать звучание интервалов. Например, с детьми часто практикуют способ ассоциаций, когда звучание интервалов сравнивают с образами животных. Различать гармонические интервалы помогает знание их разделения на консонансы и диссонансы, а мелодические интервалы часто запоминают по начальным звукам известных песен.
Давайте рассмотрим каждый из названных способов отдельно.
Метод ассоциаций (интервалы и образы животных)
Итак, у нас есть восемь основных интервалов. Их звучание нужно как-то охарактеризовать. При этом часто привлекаются образы животных. Причем важными оказываются разные детали образов: то звуки животных, то их внешний вид – размер, цвет и т.д.
Можно предложить сделать эту творческую работу самому ребенку. В этом случае нужно просто сыграть ему все интервалы по порядку и параллельно спрашивать, какое животное можно нарисовать с помощью этих звуков. Допустимо, конечно, дать и готовое решение. Оно может быть примерно следующим (можно придумать что-то другое):
В дополнение мы предлагаем скачать вам наглядное пособие для занятий с детьми темой интервалов. В приложенном файле вы найдете картинки животных и соседствующие с ними нотные записи звучащих интервалов.
ИНТЕРВАЛЫ И ЖИВОТНЫЕ В КАРТИНКАХ ДЛЯ ДЕТЕЙ – СКАЧАТЬ
Консонансы и диссонансы в музыке
Все интервалы можно разделить на две большие группы – консонансы и диссонансы. Что это значит? Консонансы – это интервалы, которые звучат слаженно, красиво, звуки в них находятся в гармонии и ладу между собой. Диссонансы – это интервалы, которые, напротив, звучат резко, несогласно, звуки в них мешают друг другу.
Существует три группы консонансов: абсолютные, совершенные и несовершенные. К абсолютным консонансам относятся чистая прима и чистая октава – всего два интервала. Совершенными консонансами являются также два интервала – чистая квинта и чистая кварта. Наконец, к числу несовершенных консонансов принадлежат терции и сексты в своих разновидностях – они бывают малые и большие.
Если вы забыли, что такое чистые, большие и малые интервалы, то повторить и разобраться можно в статье «Количественная и качественная величина интервала».
К диссонирующим созвучиям относятся все секунды и септимы, а кроме того некоторые увеличенные и уменьшенные интервалы.
Как же различать интервалы на слух, зная о консонансах и диссонансах? Нужно помнить следующие характеристики и рассуждать логически:
Запоминаем интервалы по песням
Популярный способ запоминания интервалов – учить их по началу мелодий всем известных песен или произведений классической музыки. При этом не стоит забывать, что интервалы можно брать как вверх, так и вниз. И почти на каждый случай есть какой-нибудь пример. Конечно, не на всякий интервал можно подобрать песню, но для большинства простых интервалов это работает.
Вот, что мы рекомендуем для запоминания интонаций некоторых интервалов вверх и вниз:
Интервал
Чистая прима
Бетховен «К Элизе» или Моцарт «Симфония №40»
Большая секунда
Малая терция
Детская песня «Чижик-Пыжик»
Чистая кварта
Песня о дружбе «Дружба крепкая не сломается»
Малая секста
Песня из кинофильма «Бьют часы на старой башне»
Вот такие вот примеры очень могут помочь в освоении мелодических интервалов. С широких интервалов (септим и октав) вокальные мелодии начинаются очень редко, так как они являются неудобными для интонирования. Но их всегда можно распознать по характеру звучания или методом исключения.
Таким образом, в данном выпуске мы рассмотрели с вами целый «букет» очень важных вопросов, касающихся музыкальных интервалов: сравнили гармонические и мелодические виды интервалов, выяснили, какие способы могут помочь освоению интервалов на слух. В следующих выпусках мы продолжим рассказ об интервалах, рассмотрим их на ступенях мажора и минора. До новых встреч!
Что такое консонанс?
В предыдущей заметке мы выяснили, как устроен звук. Повторим ещё раз эту формулу:
ЗВУК = ОСНОВНОЙ ТОН + ВСЕ КРАТНЫЕ ОБЕРТОНА
Кроме того, как японцы любуются на цветение сакуры, полюбуемся и мы на график АЧХ — амплитудно-частотной характеристики звука (рис. 1):
Напомним, что по горизонтальной оси отложена высота звука (частота колебаний), а по вертикальной – громкость (амплитуда).
Каждая вертикальная линия – это гармоника, первая гармоника обычно называется основным тоном. Гармоники устроены так: вторая гармоника в 2 раза выше основного тона, третья – в три, четвертая – в четыре и так далее.
Краткости ради вместо «частота n-ой гармоники» будем говорить просто «n-ая гармоника», а вместо «частота основного тона» — «частота звука».
Итак, глядя на АЧХ, нам не составит труда ответить на вопрос, что же такое консонанс.
Как досчитать до бесконечности?
Консонанс буквально означает «со-звучие», совместное звучание. Что же у двух различных звуков может звучать совместно?
Нарисуем их на одном графике друг под другом (рис. 2):
Рис. 2. Сочетание двух звуков на АЧХ
Вот и ответ: часть гармоник могут совпадать по частоте. Логично предположить, что чем больше совпадающих частот, тем больше у звуков «общего», а, следовательно, тем больше консонанса в звучании такого интервала. Если быть совсем точным, то важно не просто число совпадающих гармоник, а то, какая доля от всех звучащих гармоник совпадает, то есть отношение числа совпадающих к общему числу звучащих гармоник.
Получаем самую простую формулу для подсчета консонанса:
где Nсовп — число совпадающих гармоник, Nобщ — общее число звучащих гармоник (количество различных звучащих частот), а cons и есть наш искомый консонанс. Если быть математически корректным, то величину лучше называть мера частотного консонанса.
Проблема заключается лишь в том, что и общее число гармоник и даже число совпадающих гармоник бесконечно.
Что же получится, если мы поделим бесконечность на бесконечность?
Поменяем масштаб предыдущего графика, «отдалимся» от него (рис. 3)
Рис. 3. Сочетание двух звуков «с большого расстояния»
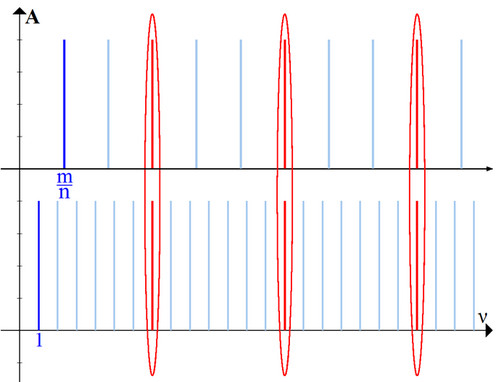
Мы видим, что совпадающие гармоники встречаются вновь и вновь. Картинка повторяется (рис. 4).
Рис. 4. Повторение структуры гармоник
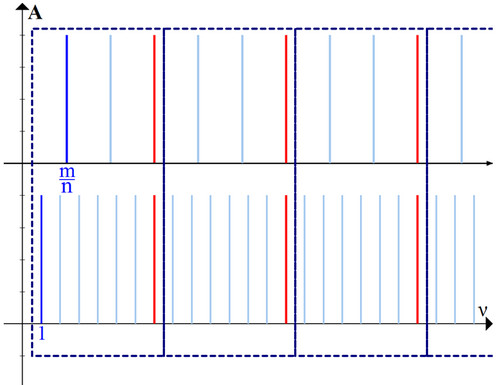
Это повторение нам и поможет.
Нам достаточно посчитать отношение (1) в одном из пунктирных прямоугольников (например, в первом), тогда из-за повторений и на всей прямой это соотношение останется таким же.
Для простоты частоту основного тона первого (нижнего) звука будем считать равной единице, а частоту основного тона второго звука запишем в виде несократимой дроби 
.
Заметим в скобках, что в нотных системах, как правило, используются именно звуки, соотношение частот которых выражается какой-либо дробью 
. К примеру, интервал квинты – это соотношение 
, кварты — 
, тритона — 
и т.д.
Посчитаем отношение (1) внутри первого прямоугольника (рис. 4).
Чему же равно общее число звучащих частот?
Будем рассуждать так.
Нужно учесть, что совпадающую частоту m мы опять посчитали два раза: когда считали частоты верхнего звука и когда считали частоты нижнего звука. Но фактически частота одна, и для правильного ответа одну «лишнюю» частоту нам нужно будет вычесть.
Итого всех звучащих частот внутри прямоугольника получится:
Подставив (2) и (4) в формулу (1), получим простое выражение для расчета консонанса:
Чтобы подчеркнуть, консонанс каких именно звуков мы рассчитали, можно указать эти звуки в скобках у cons:
С помощью такой простой формулы можно посчитать консонанс любого интервала.
А теперь рассмотрим некоторые свойства частотного консонанса и примеры его расчета.
Свойства и примеры
Для начала рассчитаем консонансы для самых простых интервалов и убедимся, что формула (6) «работает».
Какой интервал является самым простым?
Безусловно, прима. Две ноты звучат в унисон. На графике это будет выглядеть так:
Мы видим, что совпадают абсолютно все звучащие частоты. Следовательно, консонанс должен быть равен:
Теперь подставим соотношение для унисона 
в формулу (6), получим:
Расчет совпадает с «интуитивным» ответом, что и следовало ожидать.
Возьмем другой пример, в котором интуитивный ответ так же очевиден, — октаву.
В октаве верхний звук в 2 раза выше нижнего (по частоте основного тона), соответственно, на графике это будет выглядеть так:
Из графика видно, что совпадает каждая вторая гармоника, и интуитивный ответ: консонанс равен 50%.
Посчитаем его по формуле (6):
И вновь расчетная величина равна «интуитивной».
Если возьмем в качестве нижнего звука ноту до и отложим на графике величину консонанса для всех интервалов внутри октавы (простых интервалов), то получим такую картину:
Рис. 7. Расчетные меры частотных консонансов для простых интервалов от ноты до
Самые высокие показатели меры консонанса у октавы, квинты и кварты. Они исторически относились к «совершенным» консонансам. Показатели малой и большой терций, и малой и большой секст чуть ниже, эти интервалы считаются «несовершенными» консонансами. Остальные интервалы имеют более низкую меру консонанса, традиционно они относятся к группе диссонансов.
Теперь перечислим некоторые свойства меры частотного консонанса, которые исходят из формулы для её расчета:
И m и n в формуле (6) находятся в знаменателе, следовательно, при увеличении этих чисел мера консонанса уменьшается.
Если сместить обе ноты на одинаковый интервал вверх или вниз (например, построить квинту не от ноты до, а от ноты ре), то соотношение между нотами не изменится, а следовательно, и мера частотного консонанса останется прежней.
Можно было бы привести и другие свойства консонанса, но пока ограничимся этими.
Физика и лирика
Рисунок 7 даёт нам представление о том, как устроен консонанс. Но так ли мы на самом деле воспринимаем консонанс интервалов? Существуют ли люди, которым не нравятся совершенные консонансы, а самые диссонантные созвучия кажутся приятными?
Да, такие люди, безусловно, есть. И для того, чтобы это объяснить, следует разграничить два понятия: физический консонанс и консонанс воспринимаемый.
Всё, что мы рассматривали в данной статье, имеет отношение к физическому консонансу. Для его расчета необходимо знать, как устроен звук, и как складываются разные колебания. Физический консонанс даёт предпосылки для консонанса воспринимаемого, но не обуславливает его на 100%.
Консонанс воспринимаемый определяется очень просто. Человека спрашивают, нравится ли ему данное созвучие. Если да – значит, для него это консонанс, если нет – диссонанс. Если ему дают на сравнение два интервала, то можно сказать, что один из них покажется человеку в данный момент более консонансным, другой менее.
Можно ли посчитать воспринимаемый консонанс? Даже если предположить, что можно, то расчет этот будет катастрофически сложным, в него будет входить ещё одна бесконечность – бесконечность человека: его опыт, особенности слуха и способности мозга. С этой бесконечностью так просто не справиться.
Однако исследования в этой области ведутся. В частности, композитор Иван Сошинский, любезно предоставляющий аудиоматериалы для данных заметок, разработал программу, с помощью которой можно для каждого человека построить его индивидуальную карту восприятия консонансов. Сейчас ведется разработка сайта mu-theory.info, на котором любой желающий сможет пройти тестирование и узнать особенности своего слуха.
И всё же, если есть воспринимаемый консонанс, и он отличается от физического, какой же смысл в расчете последнего? Можно переформулировать этот вопрос в более конструктивном ключе: как соотносятся эти два понятия?
Исследования показывают, что корреляция между усредненным воспринимаемым консонансом и физическим консонансом порядка 80%. Это означает, что у каждого человека могут быть свои индивидуальные особенности, но подавляющий вклад в определение консонанса вносит физика звука.
Разумеется, научные изыскания в этой области находятся ещё в самом начале. И в качестве структуры звука мы взяли сравнительно простую модель кратных гармоник, и расчет консонанса применяли самый простой – частотный, и не учитывали особенности деятельности мозга по обработке звукового сигнала. Но то, что даже в рамках таких упрощений получена очень высокая степень корреляции теории и эксперимента, весьма обнадеживает и дает стимул к дальнейшим исследованиям.
Применение научного метода в области музыкальной гармонии не ограничивается расчетом консонанса, оно дает и более интересные плоды.
Например, с помощью научного метода можно музыкальную гармонию изобразить графически, визуализировать. О том, как это сделать, мы поговорим в следующий раз.