координаты точки что это такое

Координаты точки.

Положение искомой точки А в трехмерном пространстве возможно определить с помощью трех координат точки следующим образом.

Через точку А проводим плоскости АР, АQ, АR, которые соответственно параллельны полученным плоскостям YOZ, ZOX, XOY.

В местах пересечения с осями появляются точки Р, Q, R.

Числа х (абсцисса), у (ордината), z (апликата), которые показывают измеряемые отрезки OP, OQ, OR в необходимом масштабе, называются прямоугольными координатами точки А.

Координаты точки следует выбирать положительными либо отрицательными, в зависимости от того, имеют ли векторы соответственно одинаковые с основными векторами i, j, k направления или они противоположны.

Название оси z происходит от латинского слова «апликата» (applicata), т.е. «приложенная».

Точку А можно построить следующим образом:

В начале взять на плоскости XOY точку L с координатами х = ОР, y = PL, а затем «приложить» отрезок LА = z, который будет перпендикулярен плоскости XOY.

Например. Координатами точки А являются:

Вектор , берущий свое начало в точке О, к искомой точке А, является радиусом-вектором точки А и на письме обозначен буквой r. Для отличия между собой различных радиус-векторов возле буквы r ставят соответствующие значки.

Источник

Шкалы, координаты

Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.

Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.

Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).

Рисунок 1. Измерительная линейка.

Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.

Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).

Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.

Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.

Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.

Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.

Рисунок 2 Цена деления шкалы

Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?

Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:

Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.

Координатный луч, единичный отрезок, координаты точки

Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.

Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.

Рис. 3. Луч с началом в точке O

Рис. 4. Луч с равными отрезками

Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).

Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.

Рис. 5. Луч с отрезками и цифрами

Покажу еще раз на примере точки S :

так как RS=OP (по условиям построения данных отрезков),

подставив известные нам значения длины отрезков OR и OP, получим:

Значит, точке S на нашем лучу соответствует число 3.

Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.

Рис. 6. Координатный луч

Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.

Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.

Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.

Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.

Координатный луч — это не что иное, как бесконечная шкала.

Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.

Рис. 7. Разные варианты единичного отрезка

Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).

Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.

Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.

Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.

Рис. 8. Координаты точек

Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).

В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.

Рис. 9. Большие числа на координатном луче.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 4.1 / 5. Количество оценок: 8

Источник

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

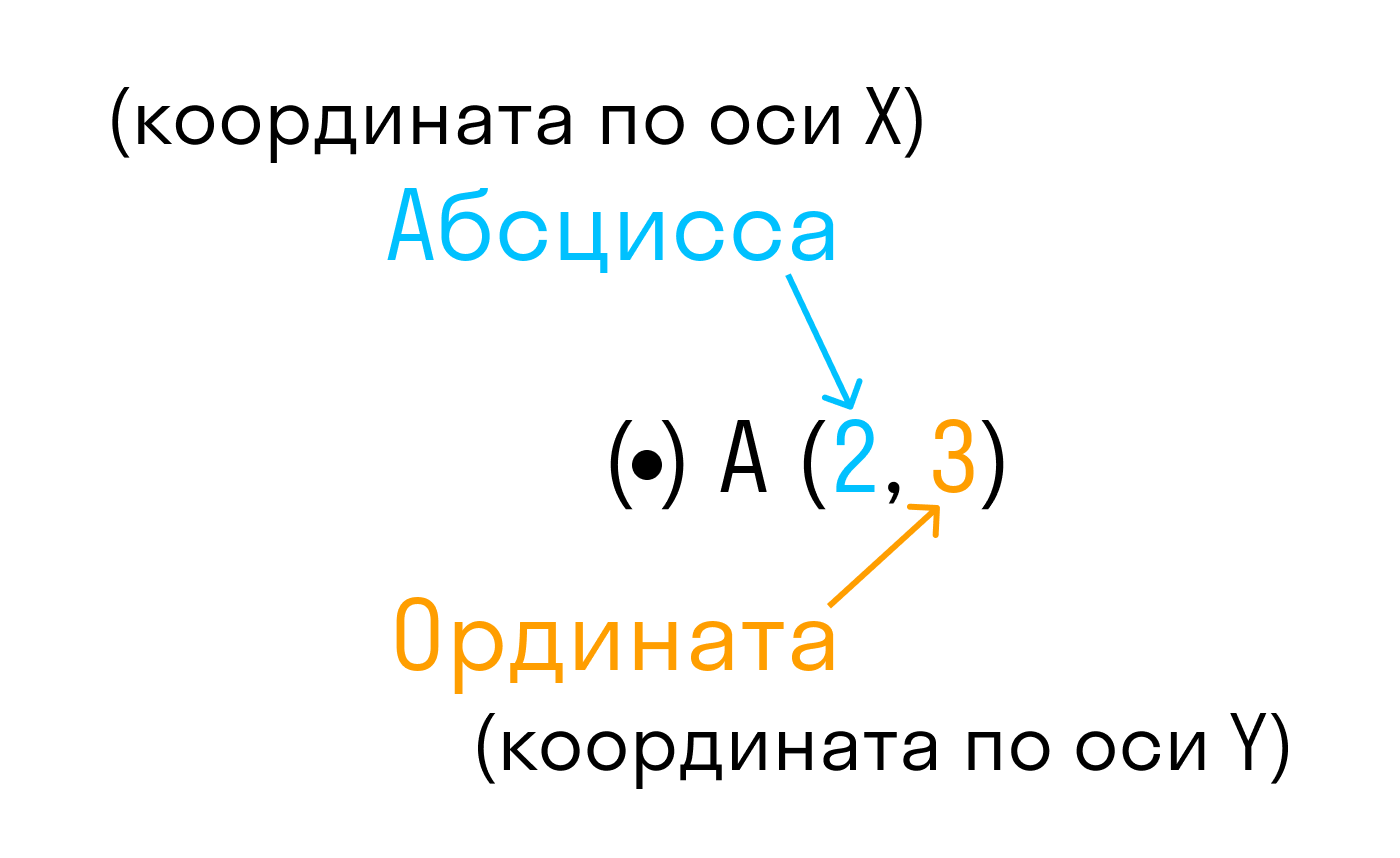
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

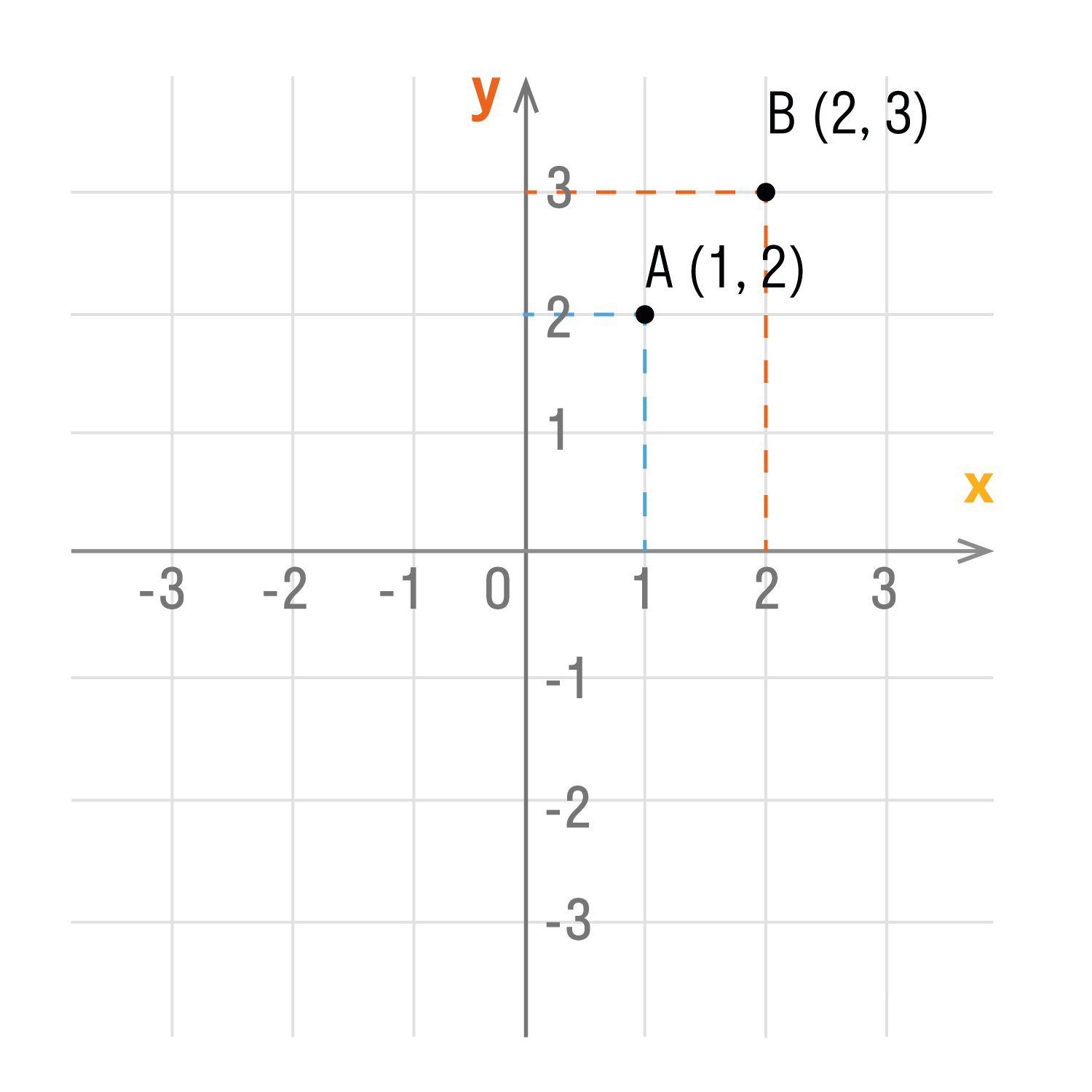
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Прямоугольная система координат в трехмерном пространстве

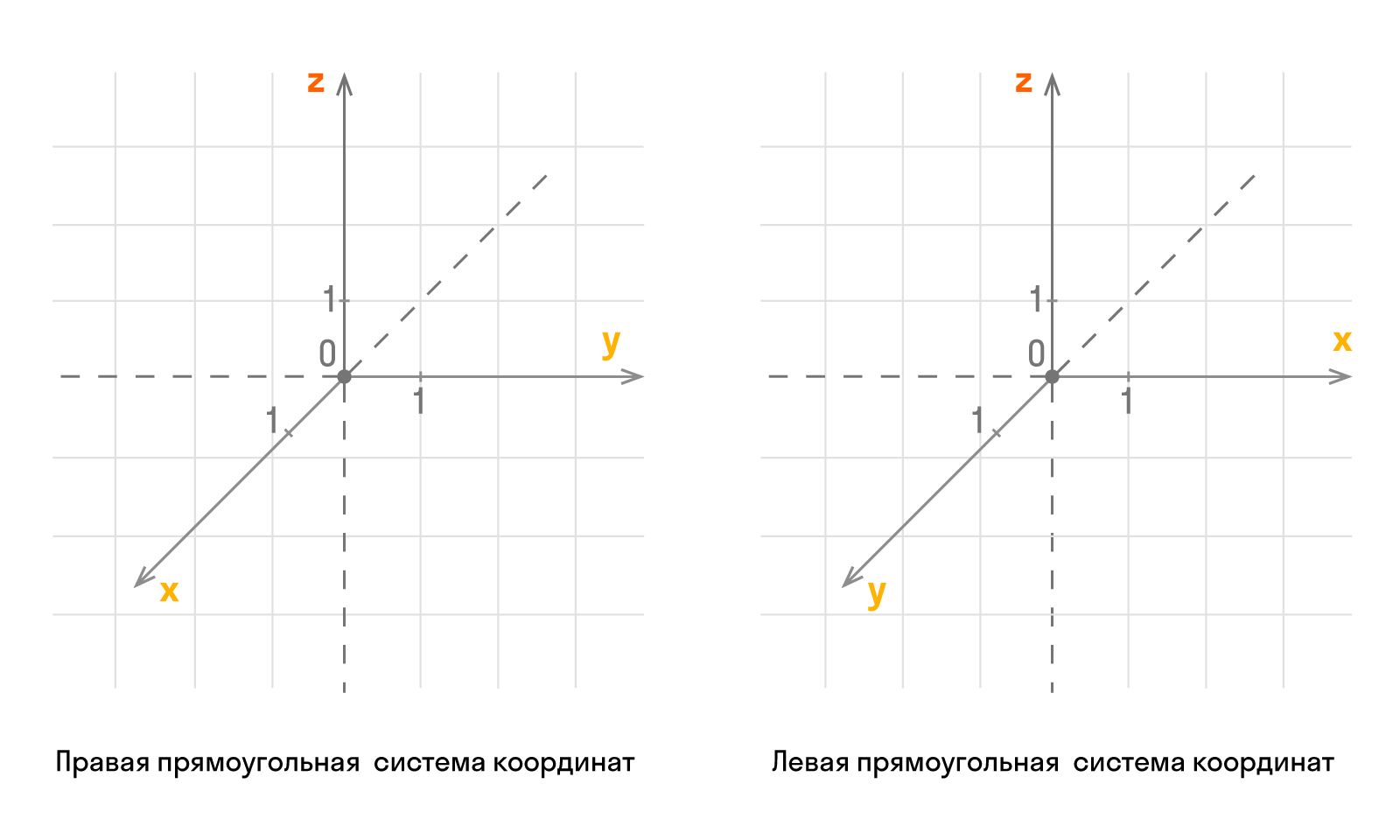
Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

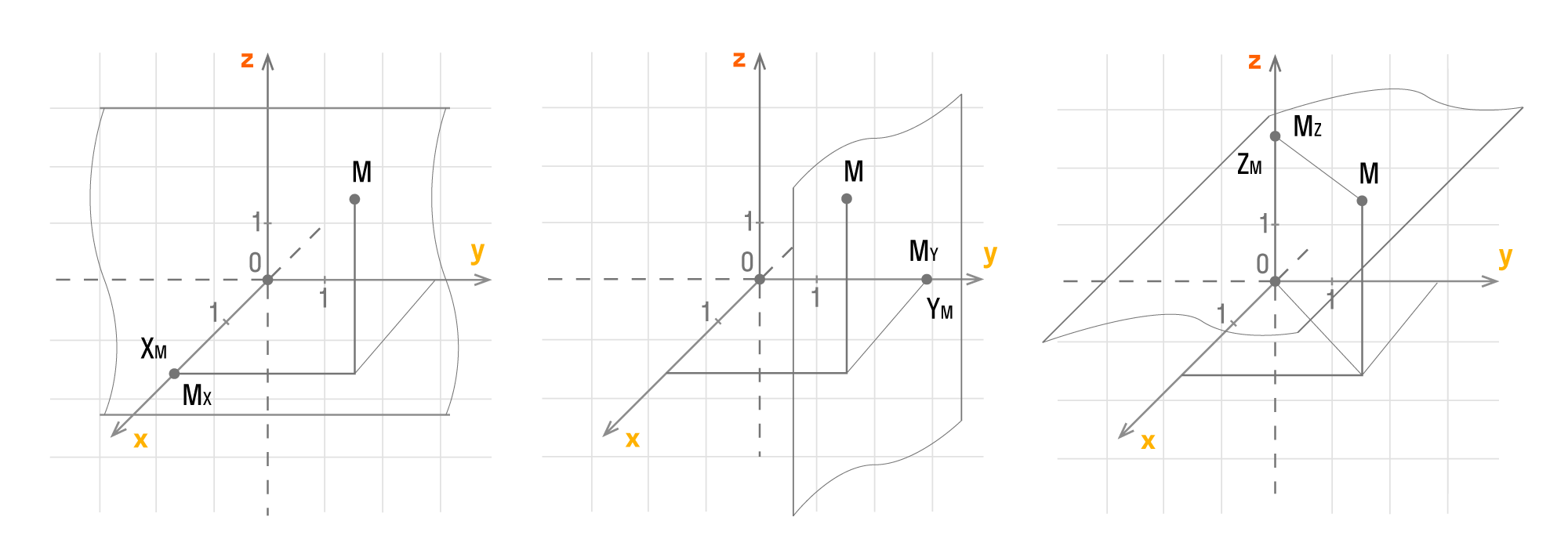
Сформулируем определение точки М в трехмерном пространстве.

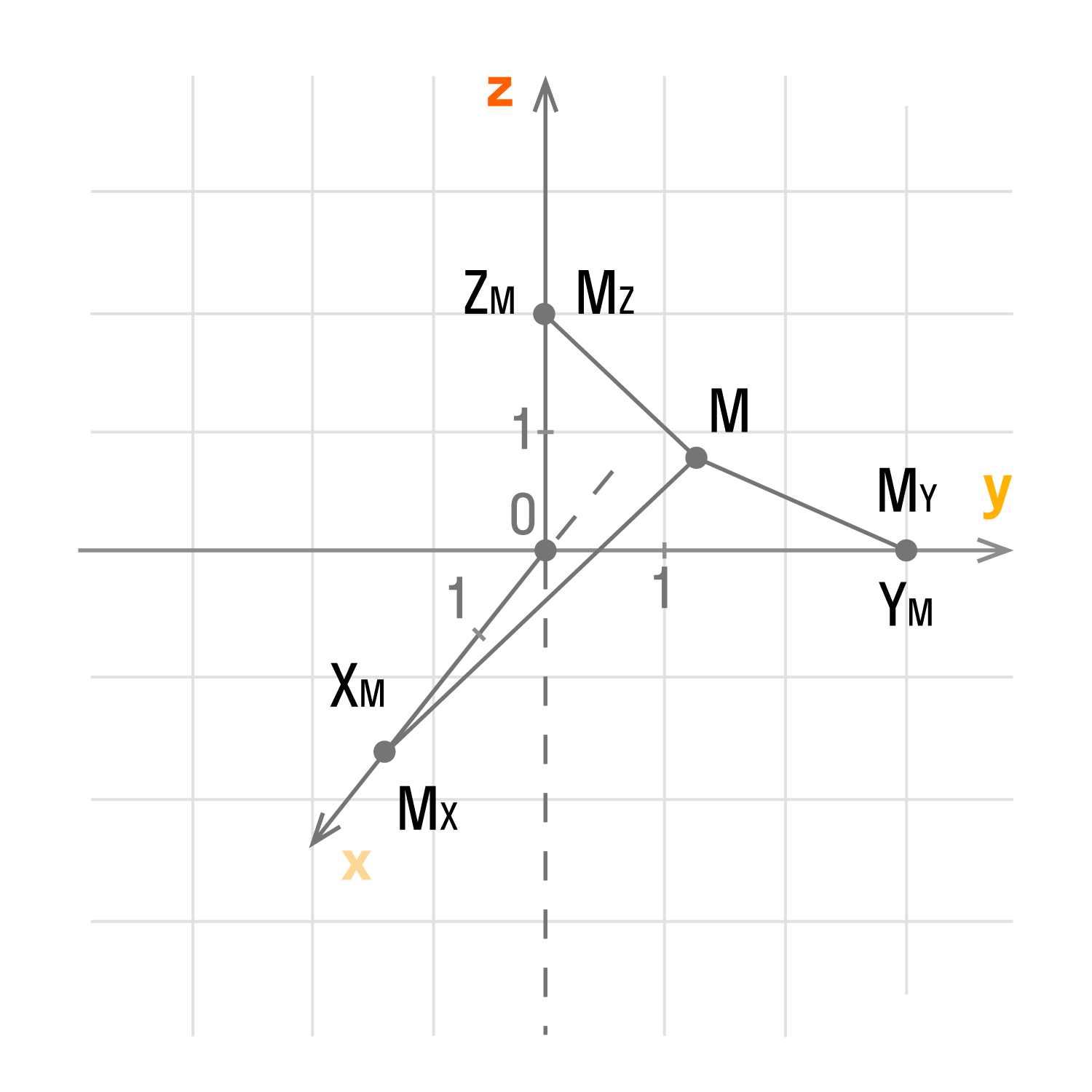
Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Источник

Координатная плоскость

Если построить на плоскости две взаимно перпендикулярные числовые оси: OX и OY, то они будут называться осями координат. Горизонтальная ось OX называется осью абсцисс (осью x), вертикальная ось OY — осью ординат (осью y).

Точка O, стоящая на пересечении осей, называется началом координат. Она является нулевой точкой для обеих осей. Положительные числа изображаются на оси абсцисс точками вправо, а на оси ординат — точками вверх от нулевой точки. Отрицательные числа изображаются точками влево и вниз от начала координат (точки O). Плоскость, на которой лежат оси координат, называется координатной плоскостью.

Оси координат делят плоскость на четыре части, называемые четвертями или квадрантами. Принято эти четверти нумеровать римскими цифрами в том порядке, в котором они пронумерованы на чертеже.

Координаты точки на плоскости

Если взять на координатной плоскости произвольную точку A и провести от неё перпендикуляры к осям координат, то основания перпендикуляров лягут на два числа. Число, на которое указывает вертикальный перпендикуляр, называется абсциссой точки A. Число, на которое указывает горизонтальный перпендикуляр, — ординатой точки A.

На чертеже абсцисса точки A равна 3, а ордината 5.

Абсцисса и ордината называются координатами данной точки на плоскости.

Координаты точки записываются в скобках справа от обозначения точки. Первой записывается абсцисса, а за ней ордината. Так запись A(3; 5) обозначает, что абсцисса точки A равна трём, а ордината — пяти.

Координаты точки – это числа, определяющие её положение на плоскости.

Начало координат — точка O — имеет и абсциссу и ординату равные нулю: O (0; 0).

Данная система координат называется прямоугольной или декартовой.

Источник