критерий вилкоксона для чего

Основные статистические критерии. Т-критерий Вилкоксона

Чтобы получить достоверные и обоснованные результаты, важно пользоваться проверенными и надежными приемами. В психологии подобрать подходящий метод непросто. Главное, учитывать все необходимые правила и требования, располагать необходимыми сведениями. Сегодня мы расскажем о непараметрическом статистическом подходе, так называемом Т-критерии Вилкоксона.

Чтобы получить достоверные и обоснованные результаты, важно пользоваться проверенными и надежными приемами. В психологии подобрать подходящий метод непросто. Главное, учитывать все необходимые правила и требования, располагать необходимыми сведениями. Сегодня мы расскажем о непараметрическом статистическом подходе, так называемом Т-критерии Вилкоксона.

Основные положения методики

Методика была разработана американским ученым, химиком, статистом Фрэнком Уилкоксоном. Ее апробация была произведена в 1945 году.

Суть методики Вилкоксона

Т-критерий Вилкоксона призван сопоставить абсолютные значения, свидетельствующие о наличии сдвига или определенной тенденции (направления).

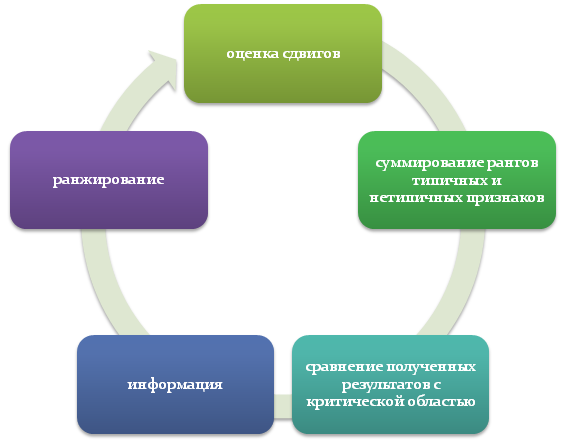
В основе метода лежит многоступенчатая обработка материалов: ранжирование, суммирование рангов, определение стабильностей и случайностей, интенсивности и пр.

Зачем нужен Т-критерий Вилкоксона?

Данная методика позволяет оценить различия между двумя признаками, рядами изменений, которые были выполнены в отношении выборки. Важным условием применения приема является то, что экспериментальная часть должна проводиться неоднократно в разное время и в разных условиях. Такой подход позволяет установить изменения не только факторов, но и их влияние на конечный результат, а также приверженность объектов исследования определенной тенденции.

Для чего применяют Т-критерий Вилкоксона?

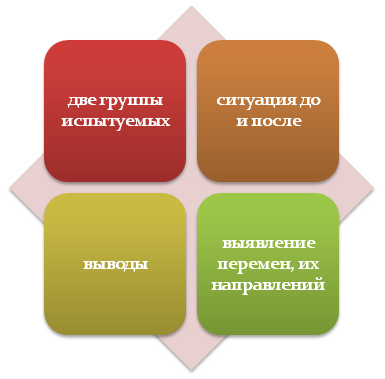
Т-критерий Вилкоксона помогает установить наличие изменений, их направление и выраженность интенсивность. С его помощью исследователь устанавливает, в каком направлении доминируют сдвиги (например, в положительную или отрицательную сторону).

Самым распространенным вариантом применения метода Вилкоксона является анализ ситуации «до» и «после» для сравнения показателей до конкретного обстоятельства/ситуации/явления и после его наступления.

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

При каких условиях Т-критерий Вилкоксона целесообразно использовать?

Рассматриваемый механизм относится к непараметрическим методам исследований. В связи с этим здесь не обязательно равномерное распределение признаков.

Важно, чтобы в качестве испытуемых принимало участие не менее 5 человек.

Параметры необходимые для применения Т-критерия Вилкоксона

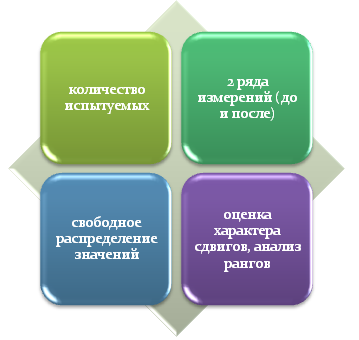
Этот алгоритм применим для сравнения количественных и качественных характеристик, в порядковой и ранговой шкале. В частности, автор научной работы может сравнивать объекты исследования на основе данных об артериальном давлении, хронических заболеваниях, привычках или по степени тяжести заболевания и пр.

Обязательным условием для применения методики Вилкоксона является наличие двух рядов измерений. Если выборок больше, то целесообразно отказаться от Т-критерия в пользу критерия Фридмана.

Как пользоваться приемом?

Существует определенная последовательность действий, позволяющая грамотно использовать данную методику.

Алгоритм использования методики

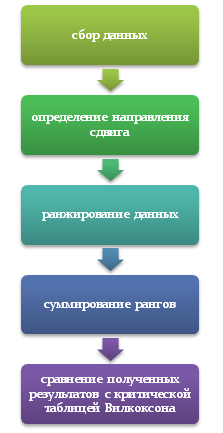
Сначала исследователю необходимо собрать необходимый для анализа материал. Здесь важно использовать не только статистические, но и экспериментальные данные (при этом проводить опыт придется неоднократно).

Далее исследователю предстоит вычислить «нулевые» сдвиги. Для этого необходимо определить начальные изменения в отношении пар испытуемых (предварительно все участники разбивают на пары, создавая две зависимые выборки). В дальнейшем они не будут учитываться. После этого следует повторно организовать эксперимент и снова вычислить сдвиги.

Затем нужно определить типичность и нетипичность выявленных изменений. Для этого нужно определить, какому направлению присуща доминанта (большая часть испытуемых).

После определения направления сдвигов и их интенсивности следует проранжировать разности пар по модулю (то есть фактический знак изменения не учитывается). Нужно расположить полученные данные в порядке возрастания.

Последним этапом при реализации Т-критерия Вилкоксона является расчет суммы рангов, относящихся к нетипичным сдвигам.

После произведенных расчетов необходимо сравнить результаты с таблицей критических значений. Если полученные данные меньше табличных, то это подчеркивает типичность признака и принимается альтернативная гипотеза.

Если же результат выше табличного, то принимается основная гипотеза.

Пример использования Т-критерия Вилкоксона

Таким образом, использование Т-критерия Вилкоксона позволяет упорядочить имеющиеся данные разбить их на две группы (до и после) и проанализировать. Результаты, получены при помощи этого приема, признаются достоверными и обоснованными, отражают общую тенденцию изучаемого явления ил признака. Чаще всего им пользуются студенты при выполнении курсовых, дипломных работ и отчетов по практике, а также соискатели ученых степеней при доказательстве выдвинутой гипотезы или проверке действия некоего закона в современных условиях.

Трудности с учебой?

Помощь в написании студенческих и
аспирантских работ!

Источник

Инструкция по использованию скрипта (FAQ)

Составлено по материалам книги: Сидоренко Е. В. «Методы математической обработки в психологии». СПб.: ООО «Речь», 2007 г.

Софья Каганович
Психолог-консультант, психодраматерапевт, психодиагност.

Владимир Каратаев
Психолог, психоаналитик.

Андрей Фетисов
Психолог, гештальт-терапевт.

Катерина Вяземская
Психолог, гештальт-терапевт, семейный терапевт.

Критерий применяется для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых.

Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.

Описание Т – критерия Вилкоксона

Суть метода состоит в том, что мы сопоставляем выраженность сдвигов в том и ином направлениях по абсолютной величине. Для этого мы сначала ранжируем все абсолютные величины сдвигов, а потом суммируем ранги. Если сдвиги в положительную и в отрицательную сторону происходят случайно, то суммы рангов абсолютных значений их будут примерно равны. Если же интенсивность сдвига в одном из направлений перевешивает, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.

Гипотезы Т – критерия Вилкоксона

H₀: Интенсивность сдвигов в типичном направлении не превосходит интенсивности сдвигов в нетипичном направлении.

H₁: Интенсивность сдвигов в типичном направлении превышает интенсивность сдвигов в нетипичном направлении.

Ограничения в применении Т – критерия Вилкоксона

2. Нулевые сдвиги из рассмотрения исключаются, и количество наблюдений n уменьшается на количество этих нулевых сдвигов (при условии, если флажок «Учитывать нулевой сдвиг?» не установлен). Можно обойти это ограничение (установив флажок «Учитывать нулевой сдвиг?»), сформулировав гипотезы, включающие отсутствие изменений, например: «Сдвиг в сторону увеличения значений превышает сдвиг в сторону уменьшения значений и тенденцию сохранения их на прежнем уровне».

Шаг 1

Введите в первую колонку данные первого замера («До»), а во вторую колонку данные второго замера («После»). Данные вводятся по одному числу на строку; без пробелов, пропусков и т.д. Вводятся только цифры. Дробные числа вводятся со знаком «.» (точка). После заполнения колонок нажмите на кнопку «Шаг 2», чтобы произвести расчет Т-критерия Вилкоксона.

Книга представляет собой практическое руководство для исследователей, поставивших целью статистически обосновать свои научные и практические выводы. Принцип отбора методов — ясность и простота. Методы рассматриваются на реальных примерах и сопровождаются алгоритмами и графическими иллюстрациями. Все они могут быть использованы для быстрой обработки данных. Руководство предназначено для психологов и специалистов в области социологии, педагогики, медицины, биологии, экономики.

Знание своего типа личности помогает лучше понимать других и себя, реализоваться в профессиональной сфере и строить более счастливые отношения с окружающими людьми.

Продолжаем раскрывать тему о самооценке. Слова «Прими это» словно говорят «довольствуйся тем, что имеешь и как живешь». Это тяжело воспринимать, как будто подразумевается отказаться от своих надежд на лучшее, от активных действий и убедить себя смириться.

Источник

Критерий Уилкоксона

Другие названия: W-критерий Вилкоксона [1], критерий знаковых рангов Вилкоксона, критерий суммы рангов Уилкоксона, Критерий Уилкоксона для связных выборок [2]

Содержание

Назначение критерия

Критерий предназначен для сопоставления показателей, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность, то есть, способен определить, является ли сдвиг показателей в одном направлении более интенсивным, чем в другом.

Описание критерия

Суть метода состоит в том, что мы сопоставляем абсолютные величины выраженности сдвигов в том или ином направлении. Для этого сначала все абсолютные величины сдвигов ранжируются, а потом суммируются ранги. Если сдвиги в ту или иную сторону происходят случайно, то и суммы их рангов окажутся примерно равны. Если же интенсивность сдвигов в одну сторону больше, то сумма рангов абсолютных значений сдвигов в противоположную сторону будет значительно ниже, чем это могло бы быть при случайных изменениях.

Ограничения критерия

Объем выборки — от 5 до 50 элементов. [источник не указан 395 дней]

Нулевые сдвиги исключаются из рассмотрения. (Это требование можно обойти, переформулировав вид гипотезы. Например: сдвиг в сторону увеличения значений превышает сдвиг в сторону их уменьшения и тенденцию к сохранению на прежнем уровне.)

Сдвиг в более часто встречающемся направлении принято считать «типичным», и наоборот.

Есть также урезанный вариант для сравнения одной выборки с известным значением медианы.

Алгоритм

Фактически оцениваются знаки значений, полученных вычитанием ряда значений одного измерения из другого. Если в результате количество снизившихся значений примерно равно количеству увеличившихся, то гипотеза о нулевой медиане подтверждается.

Примечания

Статистические показатели
Описательная статистика	Непрерывные данные Коэффициент сдвига Среднее (Арифметическое, Геометрическое, Гармоническое) · Медиана · Мода · Размах Вариация Ранг · Среднеквадратическое отклонение · Коэффициент вариации · Квантиль (Дециль, Процентиль/Перцентиль/Центиль) Моменты Математическое ожидание · Дисперсия · Асимметрия · Эксцесс Дискретные данные Частота · Таблица контингентности
Статистический вывод и проверка гипотез	Статистический вывод Доверительный интервал (Частотная вероятность) · Достоверный интервал (Байесовский вывод) · Статистическая значимость · Мета-анализ Планирование эксперимента Генеральная совокупность · Планирование выборки · Районированная выборка · Репликация · Группировка · Чувствительность и специфичность Объём выборки Статистическая мощность · Мера эффекта · Стандартная ошибка Общая оценка Байесовская оценка решения · Метод максимального правдоподобия · Метод моментов нахождения оценок · Оценка минимального расстояния · Оценка максимального интервала Статистические критерии Z-тест · t-критерий Стьюдента · Критерий Фишера · Критерий Пирсона (Хи-квадрат) · Критерий согласия Колмогорова · Тест Вальда · U-критерий Манна — Уитни · Критерий Уилкоксона · Критерий Краскела — Уоллиса · Критерий Кохрена · Критерий Лиллиефорса Анализ выживания Функция выживания · Оценка Каплана — Мейера · Логранк-тест · Интенсивность отказов · Пропорциональная модель опасностей
Корреляция	Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания
Линейные модели	Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Ковариационный анализ
Регрессия	Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия

Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами

Полезное

Смотреть что такое «Критерий Уилкоксона» в других словарях:

Критерий Уилкоксона-Манна-Уитни — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении … Википедия

Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона Манна Уитни. Критерий Краскела Уоллиса является ранговым, поэтому он инвариантен по отношению к любому… … Википедия

Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия

Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия

Критерий согласия Пирсона — Критерий Пирсона, или критерий χ² (Хи квадрат) наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая… … Википедия

Критерий Фишера — (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в… … Википедия

Критерий Лиллиефорса — статистический критерий, названный по имени Хьюберта Лиллиефорса, профессора статистики Университета Джорджа Вашингтона, являющийся модификацией критерия Колмогорова–Смирнова. Используется для проверки нулевой гипотезы о том, что выборка… … Википедия

Критерий Манна-Уитни-Уилкоксона — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении … Википедия

Критерий суммы рангов Уилкоксона — U критерий Манна Уитни (англ. Mann Whitney U test) непараметрический статистический критерий, используемый для оценки различий между двумя выборками по уровню какого либо признака, измеренного количественно. Позволяет выявлять различия в значении … Википедия

Источник

W критерий Уилкоксона

Ранжирование. Попарные разности величин признака для каждого больного ранжируются следующим образом. Положительные и отрицательные значения ставят (кроме нулевых) в один ряд так, чтобы наименьшая абсолютная величина (без учета знака) получила первый ранг, одинаковым величинам присваивают один ранг.

Отдельно вычисляют сумму рангов положительных и отрицательных разностей, меньшую из двух сумм без учета знака считают тестовой статистикой данного критерия. Нулевую гипотезу принимают при данном уровне значимости, если вычисленное значение превзойдет критической значение.

Определить нулевую и альтернативную гипотезы.

: медиана разницы в популяции равна нулю.

: медиана разницы в популяции не равна нулю.

Отобрать необходимые данные из двух взаимосвязанных выборок.

Вычислить величину статистики критерия, отвечающую H0.

Вычислите разность для каждой пары результатов. Проранжируйте все n’ ненулевые разности, присваивая ранг 1 наименьшей разности и ранг n’ — наибольшей. Сложите ранги положительных (Т+) и отрицательных (T_) разностей.

Если n’ 25, статистика критерия t принимает значение Т+ или Т_ в зависимости от того, какая из них меньше.

Если n’ > 25, рассчитайте статистику критерия z, где

которая подчиняется нормальному распределению (ее величина должна быть скорректирована, если имеется много связанных значений).

Сравнить величину статистики критерия с величинами известного распределения вероятности.

Интерпретировать значение достигнутого уровня значимости р и результаты.

Интерпретируйте значение p и рассчитайте доверительный интервал для медианы разностей.

Пример

Допустим в результате проведения исследования был вычислен ряд попарных разностей между показателем эффекта в двух попарно связанных группах (n1 = n2 = 10) (например, так называемая задача «До и после лечения»):

Ранжируем попарно разности в один ряд, независимо от знака разности, получаем следующий ранжированный ряд:

Рассчитаем отдельно сумму рангов положительных (W+) и отрицательных (W_) разностей, в нашем случае W+ = 2 + 4 + 5 + 8 + 9 + 10 = 38, W_ = 1 + 3 + 6 + 7 = 17. Для проверки двустороннего W-критерия используем меньшую статистику W_ = 17 и сравним ее с критическим значением для числа попарных разностей n = 10 и уровня значимости 5%. Такое значение равно 9. Рассчитанное минимальное значение W статистики превосходит соответствующее табличное значение, а значит нулевая гипотеза остается в силе.

В случае анализа результатов клинических исследований непараметрические критерии бывают полезны не только для анализа количественных данных, а также при качественной или альтернативной форме представления признаков.

Пример в STATISTICA

Выберите команду Непараметрическая статистика в меню Анализ для отображения стартовой панели модуля Непараметрическая статистика. Далее выберите Сравнение двух зависимых переменных и нажмите кнопку OK для отображения диалогового окна Сравнение двух переменных. В принципе, можно выполнить тест для списка переменных (точнее, списка пар); однако в данном примере мы имеем только 2 переменные.

Нажмите кнопку Переменные для отображения стандартного диалогового окна Выбор переменных, выберите переменные До лечения и После лечения.

Теперь нажмите кнопку критерий Вилкоксона, отобразится таблица результатов, показанная ниже.

Для визуализации результатов можно построить диаграмму размаха, нажав кнопку Диаграммы размаха в диалоговом окне Сравнение двух переменных. Выберите обе переменные в диалоговом окне Выбор переменных и нажмите кнопку OK. Далее, выберите тип графика в диалоге Тип диаграммы размаха. В этом примере выберите Среднее/ст.откл./ст.ош. и нажмите кнопку OK.

График ясно показывает, что переменная После лечения имеет большее среднее, чем переменная До лечения.

Источник