квантиль что это простыми словами
Квантиль
Материал из MachineLearning.
Содержание
Определение
—кванти́ль случайной величины с функцией распределения — это любое число удовлетворяющее двум условиям:
Заметим, что данные условия эквивалентны следующим:
и x_\alpha)\le 1- \alpha.» alt= «\mathbb
(\xi>x_\alpha)\le 1- \alpha.» />
Если — непрерывная строго монотонная функция, то существует единственный квантиль любого порядка который однозначно определяется из уравнения и, следовательно, выражается через функцию, обратную к функции распределения:
Кроме указанной ситуации, когда уравнение имеет единственное решение (которое и дает соответствующий квантиль), возможны также две других:
Часто используемые квантили специальных видов
Терминология, принятая в математической статистике
В задачах математической статистики часто возникает необходимость отделить сверху, снизу или с обеих сторон области, вероятности попадания в которые малы. В связи с этим часто используется следующая терминология.
Нижний (односторонний) квантиль уровня — то же, что и обычный квантиль порядка :
Верхний (односторонний) квантиль уровня — обычный квантиль порядка :
Применение квантилей в задачах проверки статистических гипотез
Если статистика с указанными свойствами существует, тогда на ее основе можно получить статистический критерий для данной задачи. Для этого необходимо с помощью соответствующих квантилей выделить область (нижнюю, верхнюю или двустороннюю), попадание в которую было бы маловероятно при нулевой гипотезе (и эта вероятность известна), однако может быть объяснено тем, что на самом деле имеет место альтернатива. Многочисленные критерии принятия решения строятся именно по такой схеме.
Применение квантилей в задачах оценивания параметров
Далее можно попробовать разрешить неравенство, стоящее под вероятностью, относительно неизвестного параметра, и переписать его в виде:
чтобы величины и зависели бы только от выборки, т.е. являлись бы статистиками. Если это удается сделать, то мы построили доверительный интервал для неизвестного параметра.
Выборочные квантили; статистическая оценка квантилей
Таким образом, выборочные квантили являются несмещёнными оценками обычных (не выборочных) квантилей.
Квантиль
Кванти́ль в математической статистике — значение, которое заданная случайная величина не превышает с фиксированной вероятностью.
Содержание
Определение
Пусть есть вероятностное пространство 
и 
— вероятностная мера, задающая распределение некоторой случайной величины 
. Пусть фиксировано 
. Тогда 
-квантилью (или квантилью уровня ) распределения называется число 
, такое что
Замечания
где 
— функция распределения .
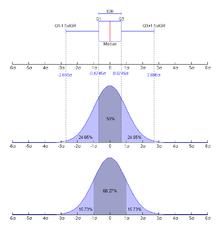
Медиана и квартили
Интерквартильным размахом (англ. Interquartile range ) называется разность между третьим и первым квартилями, то есть 
. Интерквартильный размах является характеристикой разброса распределения величины и является робастным аналогом дисперсии. Вместе, медиана и интерквартильный размах могут быть использованы вместо математического ожидания и дисперсии в случае распределений с большими выбросами, либо при невозможности вычисления последних.
Дециль
Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля.
Перцентиль
-ой перценти́лью называют квантиль уровня 
. При этом обычно рассматривают перцентили для целых , хотя данное требование не обязательно. Соответственно, медиана является 50-й перцентилью, а первый и третий квартиль — 25-й и 75-й перцентилями.
В целом, понятия квантиль и перцентиль взаимозаменяемы, также, как и шкалы исчисления вероятностей — абсолютная и процентная.
Перцентили также называются процентилями или центилями.
Квантили стандартного нормального распределения
| Вероятность, % | 99,99 | 99,90 | 99,00 | 97,72 | 97,50 | 95,00 | 90,00 | 84,13 | 50,00 |
| Квантиль | 3,715 | 3,090 | 2,326 | 2,000 | 1,960 | 1,645 | 1,282 | 1,000 | 0,000 |
См. также
Полезное
Смотреть что такое «Квантиль» в других словарях:
Квантиль — численная характеристика, применяемая в математической статистике. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
КВАНТИЛЬ — величина, характеризующая функцию распределения F(x). К. распределения порядка р, 0 Геологическая энциклопедия
квантиль — Одна из числовых характеристик случайных величин в математической статистике. БСЭ 3 … Исторический словарь галлицизмов русского языка
квантиль — 3.32 квантиль (fractile): р квантиль (квантиль уровня р или процентиль) и соответствующее значение квантили хропределяется как: F(xp) = p, (3.1) где F функция распределения для хр. Источник … Словарь-справочник терминов нормативно-технической документации
Квантиль — одна из числовых характеристик случайных величин, применяемая в математической статистике. Если функция распределения случайной величины Х непрерывна, то квантиль Kp порядка р определяется как такое число, для которого вероятность… … Большая советская энциклопедия
квантиль — Число xp, p [0,1], удовлетворяющее соотношению Pr(X Словарь социологической статистики
КВАНТИЛЬ — одна из числовых характеристик распределения вероятностей. Для действительной случайной величины Xс функцией распределения F(x)квантилью порядка р, 0 Математическая энциклопедия
КВАНТИЛЬ — одна из характеристик распределения вероятностей (см.). Лит.: Квантиль//Математическая энциклопедия. Т. 2. М. 1979. Ю.Н. Толстова … Российская социологическая энциклопедия
квантиль — квант иль, я … Русский орфографический словарь
квантиль — я, ч., мат. Одна з числових характеристик випадкових величин … Український тлумачний словник
Квантиль
Смотреть что такое «Квантиль» в других словарях:
Квантиль — численная характеристика, применяемая в математической статистике. Словарь бизнес терминов. Академик.ру. 2001 … Словарь бизнес-терминов
КВАНТИЛЬ — величина, характеризующая функцию распределения F(x). К. распределения порядка р, 0 Геологическая энциклопедия
квантиль — Одна из числовых характеристик случайных величин в математической статистике. БСЭ 3 … Исторический словарь галлицизмов русского языка
квантиль — 3.32 квантиль (fractile): р квантиль (квантиль уровня р или процентиль) и соответствующее значение квантили хропределяется как: F(xp) = p, (3.1) где F функция распределения для хр. Источник … Словарь-справочник терминов нормативно-технической документации
Квантиль — в математической статистике значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Содержание 1 Определение 2 Замечания 3 Медиан … Википедия
квантиль — Число xp, p [0,1], удовлетворяющее соотношению Pr(X Словарь социологической статистики
КВАНТИЛЬ — одна из числовых характеристик распределения вероятностей. Для действительной случайной величины Xс функцией распределения F(x)квантилью порядка р, 0 Математическая энциклопедия
КВАНТИЛЬ — одна из характеристик распределения вероятностей (см.). Лит.: Квантиль//Математическая энциклопедия. Т. 2. М. 1979. Ю.Н. Толстова … Российская социологическая энциклопедия
квантиль — квант иль, я … Русский орфографический словарь
квантиль — я, ч., мат. Одна з числових характеристик випадкових величин … Український тлумачний словник
Обсудив меры центральной тенденции, рассмотрим подход к описанию положения статистических данных, который включает в себя определение пороговых значений, в пределах которых лежат указанные пропорции данных.
Мы знаем, что медиана делит распределение пополам. Мы можем определить другие разделительные линии, которые разбивают распределение на меньшие части.
Например, первый квартиль \(Q_1\) делит распределение так, что 25 процентов наблюдений лежат не выше него; следовательно, 1-й квартиль также является 25-м процентилем.
Второй квартиль \(Q_2\) представляет 50-й процентиль, а третий квартиль \(Q_3\) представляет 75-й процентиль, потому что 75 процентов наблюдений лежат не выше него.
Имея дело с фактическими данными, мы часто обнаруживаем, что нам нужно найти приблизительное значение процентиля. Например, если нас интересует значение 75-го процентиля, мы можем обнаружить, что ни одно наблюдение не разделяет выборку так, что ровно 75 процентов наблюдений лежат не выше этого значения.
Следующая процедура, однако, может помочь нам определить или оценить процентиль. Процедура включает в себя сначала определение положения процентиля в наборе наблюдений, а затем определение (или оценку) значения, связанного с этой позицией.
Формула для позиции процентиля в массиве из n записей, отсортированных по возрастанию:
\(\large \dst
L_y = (n+1) \frac
Значение \(L_y\) может быть или не быть целым числом.
Как правило, по мере увеличения размера выборки результат расчета положения в процентилях становится более точным; в небольших выборках он может быть весьма приблизительным.
В качестве примера случая, когда \(L_y\) не является целым числом, предположим, что мы хотим определить 3-ий квартиль доходности за 2012 год (\(Q_3\) или \(P_<75>\)) для 16 европейских фондовых рынков, представленных в Таблице 8.
В соответствии с Формулой 8 позиция третьего квартиля имеет вид \(L_<75>\) = (16 + 1) (75/100) = 12.75 или между 12-м и 13-м позициями в Таблице 9, в которой доходность представлена в порядке возрастания.
Определив «0.75» как «12.75», мы пришли бы к выводу, что \(P_<75>\) находится на 75% расстояния между 15.90% и 20.72%.
Подведем итоги:
1) Когда позиция \(L_y\) представляет собой целое число, она соответствует фактическому наблюдению. Например, если бы Дания не была включена в выборку, то \(n + 1\) было бы равно 16, а при \(L_<75>\) = 12 третий квартиль был бы \(P_ <75>= X_<12>\), где \(X_i\) определяется как значение наблюдения в \(i\)-й \((i = L_<75>)\) позиции данных, отсортированных в порядке возрастания (т. е. \(P_<75>\) = 15.90).
Возвращаясь к расчету \(P_<75>\) для доходности капитала, мы обнаружили, что \(L_y\) = 12.75; следующее более низкое целое число равно 12, а следующее более высокое целое число равно 13.
Используя линейную интерполяцию, находим:
Как указано выше, на 12-й позиции находится доходность акций Франции, поэтому \(X_<12>\) = 15.90%; \(X_<13>\) = 20.72%, что соответствует доходности акций Австрии.
Таким образом, наша оценка методом линейной интерполяции составит:
Мы следуем этой схеме всякий раз, когда \(L_y\) не является целым числом: ближайшие целые числа ниже и выше \(L_y\) устанавливают позиции наблюдений, которые ограничивают \(P_y\), а затем используются для интерполяции.
Пример, приведенный ниже иллюстрирует расчет различных квантилей для дивидендной доходности компонентов основного европейского индекса акций.
Пример расчета процентилей, квартилей и квинтилей.
Рыночная капитализация ранжируется в порядке возрастания.