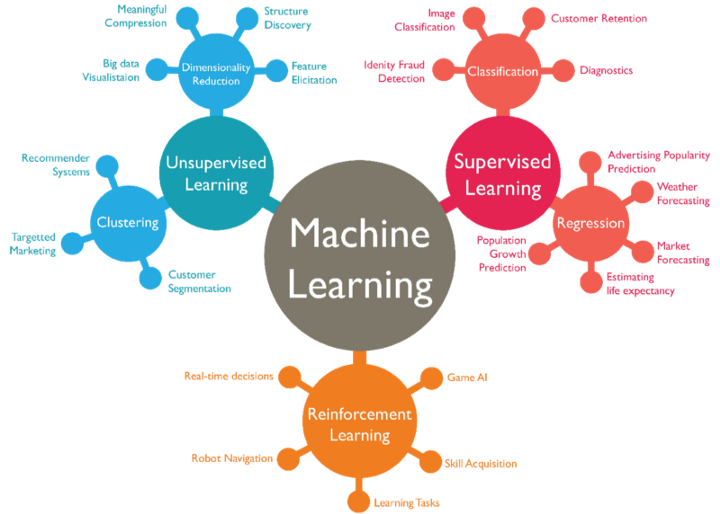
логистическая регрессия что это такое
Логистическая регрессия для чайников: подробное объяснение
Дата публикации Aug 14, 2019
Хотел бы начать это путешествие ML с этим сообщением:
«Постарайтесь сначала понять формулировку проблемы, оставив в стороне свой тренированный интеллект, и попытайтесь проанализировать данные, как будто вы ничего о них не знаете. Ваше честное признание того, что вы ничего не знаете, приведет вас к процессу создания модели, достойной развертывания. «
Процесс важнее, чем результат в области науки о данных
В нашей последней статье о контролируемом ML мы рассмотрели модель линейной регрессии, которая имела дело с непрерывными атрибутами, чтобы определить влияние независимой переменной на зависимую переменную. Я бы пригласил вас пройти через это, чтобы получить правильный контекст.
Машинное обучение под наблюдением с использованием линейной регрессии: Часть 1
Понимание модели линейной регрессии
towardsdatascience.com
Все упражнение в модели линейной регрессии состояло в том, чтобы найти наилучшую линию соответствия, которая может предсказать влияние независимой переменной на зависимую или целевую переменную. Линейная регрессия имеет дело с проблемой, где нам нужно предсказать
Здесь мы пытаемся предсказать влияние / изменения, наблюдаемые на целевые переменные продажи / производительность, исходя из рабочего времени / возраста. Как насчет проблемы, когда мы хотим четко предсказать на основе входных данных, вероятность того, что пациенты будут диабетиками или не диабетиками, или предсказать вероятность того, что собака будет лаять в середине ночи или нет.
Проблема такого типа, когда нам нужно найти вероятность того, что событие произойдет или нет, или же оно будет истинным / ложным, называется проблемой классификации. Чтобы решить эту проблему, мы часто используем один из самых популярныхмодель ML под наблюдениемназывается,Модель логистической регрессии.
С этой информацией давайте начнем сегодняшнюю сессию по логистической регрессии, где мы рассмотрим
Что такое логистическая регрессия?
Логистическая регрессияэто статистический метод для анализа набора данных, в котором есть одна или несколько независимых переменных, которые определяют результат. Результат измеряется с помощью дихотомической переменной (в которой есть только два возможных результата). Он используется для прогнозирования двоичного результата (1/0, Да / Нет, Истина / Ложь) с учетом набора независимых переменных.
Вы также можете рассматривать логистическую регрессию как особый случай линейной регрессии, когда исходная переменная является категориальной, где мы используем логарифм шансов в качестве зависимой переменной. Проще говоря, он предсказывает вероятность возникновения события путем подгонки данных клогитфункция.
Помните, что в некоторых случаях зависимые переменные могут иметь более двух результатов, например, в браке / не замужем / в разводе, такие сценарии классифицируются какполиномиальная логистическая регрессия.Хотя они работают одинаково, чтобы предсказать результат.
Несколько знакомых примеров логистической регрессии:
Некоторые выдающиеся примеры, такие как:
Как работает логистическая регрессия?
Логистическая модель: сигмовидная функция
Давайте попробуем понять логистическую регрессию, понимая логистическую модель. Как и в случае линейной регрессии, давайте представим нашу гипотезу (Предсказание зависимой переменной) в классификации. В классификации наше представление гипотезы, которое пытается предсказать двоичный результат или o или 1, будет выглядеть так:
hθ (x) = g (θ T x) = 1/1 + e − θ T x,
Здесь g (z) = 1 / (1 + e ^ −z) называется lОгистическая функция или сигмовидная функция:
(г): представление логистической функции, которую мы также называем сигмовидной функцией. Из приведенного выше визуального представления сигмовидной функции мы можем легко понять, как эта кривая описывает многие реальные ситуации, такие как рост населения. На начальных этапах это показывает экспоненциальный рост, но через некоторое время, из-за конкуренции за определенные ресурсы (горлышко бутылки), скорость роста снижается, пока не достигнет тупиковой ситуации, и рост не будет
Вопрос здесь в том, как этологит(сигмоидальная функция) помогает нам определить вероятность классификации данных по различным классам. Давайте попробуем понять, как рассчитывается наша функция logit, что даст нам некоторую ясность
Математика за логистической функцией:
Шаг 1: Классификация входных данных должна быть в классе ноль или единица.
Во-первых, нам нужно вычислить вероятность того, что наблюдение принадлежит классу 1 (мы также можем назвать его положительным классом), используя функцию логистического отклика. В этом случае наш параметр z, как видно из приведенной ниже функции logit.
Log Odds (функция Logit):
Вышеприведенное объяснение также может быть понято с точки зрения логарифмических коэффициентов, что является своего рода пониманием вероятности классификации элементов на классы (1 или 0) с помощьюСТАВКИ:
Эти шансы, которые напоминают сходство с линейной регрессией, называютсялогит.
logit (P) = a + bX,
Шаг 2: Определение граничных значений для шансов
Теперь мы определим границу порога, чтобы четко классифицировать каждое заданное входное значение в один из классов.
Мы можем выбрать пороговое значение в соответствии с бизнес-проблемой, которую мы пытаемся решить, как правило, которая находится в районе 0,5 Таким образом, если ваши значения вероятности окажутся> 0,5, мы можем классифицировать такое наблюдение в тип класса 1, а остальные в класс 0.Выбор порогового значения обычно основывается на типах ошибок, которые бывают двух типов:ложные срабатывания и ложные отрицания.
Ложно-положительная ошибка возникает, когда модель прогнозирует класс 1, но наблюдение фактически принадлежит классу 0. Ложно-отрицательная ошибка допускается, когда модель прогнозирует класс 0, но наблюдение фактически принадлежит классу 1. Идеальная модель будет классифицировать все правильно классифицирует: все 1 (или истины) как 1, и все 0 (или ложь) как 0. Таким образом, мы имели бы FN = FP = 0.
Влияние пороговых значений:
1.Более высокое пороговое значение
Предположим, если P (y = 1)> 0,7. Модель является более строгой при классификации как 1, и, следовательно, будет сделано больше ошибок ложного отрицания.
2. Нижнее пороговое значение:
Предположим, если P (y = 1)> 0,3.
Модель теперь менее строгая, и мы классифицируем больше примеров как класс 1, поэтому мы делаем больше ошибок ложных срабатываний.
Путаница Матрица: путь к Choose Эффективное пороговое значение:
Матрица путаницы, также известная как матрица ошибок, является предиктором производительности модели для задачи классификации. Количество правильных и неправильных прогнозов суммируется со значениями количества и разбивается по каждому классу. Это лежит в основе путаницы.
Матрица путаницы показывает, каким образом ваша модель классификации находится в замешательстве, когда она делает прогнозы для наблюдений, она помогает нам измерить тип ошибки, которую делает наша модель, при классификации наблюдения по различным классам.
Ключевые части матрицы путаницы:
Ключевые показатели обучения из матрицы путаницы:
Матрица путаницы помогает нам изучать следующие метрики, помогая нам измерять производительность логистической модели.
Точность:
В целом, как часто верен классификатор?
Точность = (TP + TN) / общее количество засекреченных предметов = (TP + TN) / (TP + TN + FP + FN)
Точность:
Когда это предсказывает да, как часто это правильно?
Точность обычно используется, когда целью являетсяограничить количество ложных срабатываний(ФП). Например, с помощью алгоритма фильтрации спама, где наша цель состоит в том, чтобы свести к минимуму количество реальных электронных писем, которые классифицируются как спам
Точность = TP / (TP + FP)
Отзыв:
Когда это на самом деле положительный результат, как часто он предсказывает правильно?
Напомним = TP / (TP + FN), также известный как чувствительность.
f1-счет:
Это просто гармоническое среднее точности и напоминания:
f1-оценка = 2 * ((точность * отзыв) / (точность + отзыв))
Поэтому, когда вам нужно принять во внимание как точность, так и вспомнить, этот показатель f1 является полезным показателем для измерения. Если вы попытаетесь оптимизировать только отзыв, ваш алгоритм будет предсказывать, что большинство примеров будет принадлежать положительному классу, но это приведет к множеству ложных срабатываний и, следовательно, к низкой точности. Кроме того, если вы попытаетесь оптимизировать точность, ваша модель будет предсказывать очень мало примеров как положительные результаты (те, которые имеют наибольшую вероятность), но отзыв будет очень низким. Так что может быть полезно сбалансировать и рассмотреть оба варианта и увидеть результат.
Площадь AUC под кривой:
Специфичность или истинный отрицательный показатель= TN / (TN + FP)
Чувствительность или истинно положительный показатель= TP / (TP + FN)
ТакFPR, ложноположительный показатель = 1 – специфичность
Интуиция за кривой ROC:
Эта модель, которая предсказывает случайно, будет иметь ROC-кривую, которая выглядит как диагональная зеленая линия (как показано выше на рисунке). Это не дискриминационная модель. Чем дальше кривая от диагональной линии, тем лучше модель различает положительные и отрицательные значения в целом.
Типы логистической регрессии:
Поскольку мы поняли некоторые важные оговорки, связанные с логистической регрессией, пришло время взять некоторое практическое понимание на простом примере:
Реализация логистической регрессии:
Мы собираемся охватить это упражнение по созданию модели в следующие шаги:
Основная цель: прогнозировать диабет с использованием классификатора логистической регрессии.
1. Загрузка данных:
Мы будем использоватьНабор данных индийского диабета Pima, полученный из kaggle, Пожалуйста, загрузите данные из следующихссылка:
Напишите / скопируйте приведенный ниже код и запустите его в своем блокноте Juypter (убедитесь, что вы установилианаконда дистрибуцияв вашей системе), когда вы запустите этот фрагмент кода, вы увидите вывод, как показано на рис. 1.0
Исследовательский анализ данных:
Давайте изучим данный набор данных, чтобы найти
Анализ нечисловых и нулевых значений:
Напишите следующий фрагмент кода и скомпилируйте его:
Выход:
Вы обнаружите, что нет нечисловых атрибутов, так как возвращаемый массив имеет пустые значения индекса для каждого столбца.
Описательный анализ:
Давайте проведем некоторый описательный анализ, чтобы найти
Мы можем проанализировать каждый столбец с помощью пандописывают ()метод, чтобы получить статистическую сводку всех атрибутов. Этот анализ помогает нам определить, какой столбец сильно искажен, как выглядят хвосты, каковы средние, срединные и квартильные значения каждого столбца.
Запишите / скопируйте следующий код в свой блокнот и скомпилируйте его:
Быстрое наблюдение:
Давайте разберемся подробнее со всеми атрибутами dataframe, используя визуализацию парных участков.
Анализ парных участков.
Давайте посмотрим на целевой столбец ‘учебный классЧтобы понять, как данные распределяются между различными значениями.
Ключевые идеи:
Логистическая модель с использованием SkLearn & Python:
Импортные пакеты Sklearn:
ИмпортироватьЛогистическая регрессиямодель и другие необходимые пакеты, отsklearnпакет Python, как показано ниже:
Разделить данные на данные обучения и испытаний:
Давайте построим нашу модель:
Давайте посмотрим, как наша модель маркирует данные X_train, чтобы сделать классификацию:
Вы можете видеть, что с помощью функции model.predict (X_test) наша модель классифицировала каждый атрибут столбца (X-train) как 0/1 как прогноз
Время, чтобы измерить, как модель выступила (забил)
Перед этим давайте выясним значения коэффициентов плоскости (поверхности), которую наша модель нашла в качестве поверхности наилучшего соответствия, используя приведенный ниже код:
Который, получить в нашей функции сигмовидной
сигмоид, g (z) = 1 / (1 + e ^ −z).
Оценка модели:
Давайте посмотрим, как наша модель наилучшего соответствия сравнивается с нетренированными тестовыми данными, используя основную логистическую функцию (сигмовидная функция) мы обсуждали выше.
Показатель модели составляет 0,774, что в пересчете на процент составляет 77,4%. Это не на высоте. Кроме того, здесь необходимо указать, что ранее мы обсуждали, как диабетический класс был недостаточно представлен по сравнению с недиабетическим классом с точки зрения выборочных данных, поэтому мы должны редко полагаться на эту модель и проводить дальнейшие измерения с использованием метрик уровня класса матриц смешения. (Напомним, точность и т. Д.)
Давайте измерим производительность модели с помощью Confusion Metrics:
Наблюдение:
Давайте вычислим значение отзыва: показатель уровня класса для измерения производительности модели:
Отзыв:
Отзыв(Для недиабетических) = TP / (TP + FN)
Напомним = 132 / (132 + 14) = 132/146 = 0,90 = 90%
Отзыв(Для диабетиков) = TP / (TP + FN)
Напомним (для диабетиков) = 47/85 = 0,55 = 55%,
Эта модель работает плохо в случае диабетика, что вполне заметно из-за отсутствия доступных образцов данных для диабетического класса для моделирования, как мы обсуждали ранее.
Точность:
что является низким, особенно учитывая природу проблемы (здесь отрасль здравоохранения), которую мы пытаемся решить, где ожидается точность более 95%.
Что дальше?
Закрытие:
Хотелось бы закончить эту часть «Логистической регрессией» пищей для размышлений
Никогда не доверяйте тому, что вы знаете, вместо того, чтобы задавать вопросы и найти ответ для себя.
Алгоритмы машинного обучения простым языком. Часть 3
Jun 8, 2019 · 5 min read
Логистическая регрессия
Итак, мы уже познакомились с линейной регрессией. Она определяла влияние переменных на другую переменную при условии, что: 1) результирующая переменная непрерывна и 2) отношение между независимыми переменными и результирующей линейное.
Но что, если результирующая переменная категориальная? Тогда и приходит на помощь логистическая регрессия!
Категориальные переменные — те, которые могут принимать лишь значения, обозначающие определённую категорию. Например, дни недели. Если у тебя есть точки на графике, обозначающие события определённого дня, то ни одна точка не может быть между понедельником и вторником. Если что-то произошло в понедельник, то оно произошло в понедельник, всё просто.
Те п ерь, если мы вспомним, как работает линейная регрессия, то как вообще можно определить линию наилучшего соответствия для чего-то категориального? Это невозможно! Поэтому логистическая регрессия выдаёт не численное значение, а вероятность соответствия той или иной категории. Поэтому модели, использующие логистическую регрессию, чаще всего используются для классификации.
Логистическая функция нелинейна. Как тогда логистическая регрессия может быть линейным классификатором?
Многомерная логистическая функция задаёт поверхность, которая поднимается от озёрной ложи (в точке ноль) к плато (в точке 1). Если вы заполните озеро до значения 0,5, то береговая линия будет прямой. Эта прямая и есть разделительная прямая для классификатора. В этом смысле логистическая регрессия — это линейный классификатор. Она работает лучше всего с линейно разделимыми классами”.
Вернёмся к тому, что мы называем линейную и логистическую регрессию “линейными”. Где же линейная часть логистической регрессии, когда мы не можем определить линию наилучшего соответствия? В мире логистической регрессии результирующая переменная находится в линейных отношениях с логарифмом отношения шансов независимых переменных.
Отношение шансов
Ядро логистической регрессии=отношение шансов.
Отношение шансов — это отношение вероятности успешного исхода к вероятности провала. Другими словами, это отношение вероятности того, что событие произойдёт, к вероятности того, что оно не произойдёт.
Для конкретного примера давай рассмотрим школьников, которые пишут тест. Известно, что для девушек отношение шансов того, что они сдадут тест, 5:1, а для парней — 3:10. Это значит, что из 6 девушек 5 скорее всего успешно сдадут тест, а из 13 парней — всего лишь 3. Общее количество учеников равно 19.
То есть отношение шансов и вероятность — одно и то же?
Нет. Вероятность — это отношение количества раз, когда произошло конкретное событие, к количеству всех произошедших событий (например, из 30 подбрасываний монетки в 10 случаях выпала решка).
Отношение шансов — это отношение количества раз, когда произошло конкретное событие, к количеству раз, когда оно не произошло (из 30 подбрасываний в 10 случаях выпала решка, значит, в 20 она не выпала, тогда отношение шансов — 10:20).
Это значит, что вероятность всегда будет в пределах от нуля до единицы, тогда как отношение шансов может расти от нуля до бесконечности. Это проблема для модели логистической регрессии, так как ожидаемые выходные данные должны быть вероятностью, то есть числом в промежутке от нуля до единицы.
Как получить вероятность из отношения шансов?
Давай рассмотрим это на определённой задаче классификации. Например, победит ли твоя любимая футбольная команда в матче с другой командой. Предположим, что отношение шансов того, что твоя любимая команда проиграет — 1:6 или 0,17, а того, что выиграет — 6:1 или 6. Эти числа можно представить на числовой прямой таким образом:
Скорее всего, ты не хочешь, чтобы модель ориентировалась только на модуль отношений шансов. Нужно, чтобы она учитывала, допустим, погоду, игроков и так далее. Для того, чтобы равномерно (симметрично) распределить модуль отношения шансов, мы вычисляем логарифм отношения шансов.
Логарифм отношения шансов
Это натуральный логарифм из отношения шансов. Когда ты берёшь натуральный логарифм от каких-то значений, ты делаешь их более нормально распределёнными. Когда что-то имеет нормальное распределение, с ним очень легко работать.
Когда мы берём натуральный логарифм от отношения шансов, мы распределяем значения от отрицательной бесконечности до положительной. Ты можешь увидеть это на кривой Белла.
Хоть нам и до сих пор нужно число в промежутке от 0 до 1, достигнутая симметрия приближает нас к получению верного результата.
Логит-функция
Это функция, с помощью которой мы получаем логарифм отношения шансов.
Логистическая регрессия и ROC-анализ — математический аппарат
Математический аппарат и назначение бинарной логистической регрессии — популярного инструмента для решения задач регрессии и классификации. ROC-анализ тесно связан с бинарной логистической регрессией и применяется для оценки качества моделей: позволяет выбрать аналитику модель с наилучшей прогностической силой, проанализировать чувствительность и специфичность моделей, подобрать порог отсечения.
Введение
Логистическая регрессия — полезный классический инструмент для решения задачи регрессии и классификации. ROC-анализ — аппарат для анализа качества моделей. Оба алгоритма активно используются для построения моделей в медицине и проведения клинических исследований.
Логистическая регрессия получила распространение в скоринге для расчета рейтинга заемщиков и управления кредитными рисками. Поэтому, несмотря на свое «происхождение» из статистики, логистическую регрессию и ROC-анализ почти всегда можно увидеть в наборе Data Mining алгоритмов.
Логистическая регрессия
Логистическая регрессия — это разновидность множественной регрессии, общее назначение которой состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Бинарная логистическая регрессия применяется в случае, когда зависимая переменная является бинарной (т.е. может принимать только два значения). С помощью логистической регрессии можно оценивать вероятность того, что событие наступит для конкретного испытуемого (больной/здоровый, возврат кредита/дефолт и т.д.).
Все регрессионные модели могут быть записаны в виде формулы:
y = F (x_1,\, x_2, \,\dots, \, x_n)
В множественной линейной регрессии предполагается, что зависимая переменная является линейной функцией независимых переменных, т.е.:
Можно ли ее использовать для задачи оценки вероятности исхода события? Да, можно, вычислив стандартные коэффициенты регрессии. Например, если рассматривается исход по займу, задается переменная y со значениями 1 и 0, где 1 означает, что соответствующий заемщик расплатился по кредиту, а 0, что имел место дефолт.
Для решения проблемы задача регрессии может быть сформулирована иначе: вместо предсказания бинарной переменной, мы предсказываем непрерывную переменную со значениями на отрезке [0,1] при любых значениях независимых переменных. Это достигается применением следующего регрессионного уравнения (логит-преобразование):
где P — вероятность того, что произойдет интересующее событие e — основание натуральных логарифмов 2,71…; y — стандартное уравнение регрессии.
Рис. 1 — Логистическая кривая
P’ = \log_e \Bigl(\frac
<1-P>\Bigr)
Это преобразование обычно называют логистическим или логит-преобразованием. Теоретически P’ может принимать любое значение. Поскольку логистическое преобразование решает проблему об ограничении на 0-1 границы для первоначальной зависимой переменной (вероятности), то эти преобразованные значения можно использовать в обычном линейном регрессионном уравнении. А именно, если произвести логистическое преобразование обеих частей описанного выше уравнения, мы получим стандартную модель линейной регрессии.
Существует несколько способов нахождения коэффициентов логистической регрессии. На практике часто используют метод максимального правдоподобия. Он применяется в статистике для получения оценок параметров генеральной совокупности по данным выборки. Основу метода составляет функция правдоподобия (likehood function), выражающая плотность вероятности (вероятность) совместного появления результатов выборки
L\,(Y_1,\,Y_2,\,\dots,\,Y_k;\,\theta) = p\,(Y_1;\, \theta)\cdot\dots\cdotp\,p\,(Y_k;\,\theta)
L\,*\,(Y;\,\theta) = \ln\,(L\,(Y;\,\theta)\,) \rightarrow \max
Логарифмическая функция правдоподобия равна:
Можно показать, что градиент g и гессиан H функции правдоподобия равны:
g = \sum_i (Y_i\,-\,P_i)\,X_i
H=-\sum_i P_i\,(1\,-\,P_i)\,X_i^T\,X_i\,\leq 0
Гессиан всюду отрицательно определенный, поэтому логарифмическая функция правдоподобия всюду вогнута. Для поиска максимума можно использовать метод Ньютона, который здесь будет всегда сходиться (выполнено условие сходимости метода):
Логистическую регрессию можно представить в виде однослойной нейронной сети с сигмоидальной функцией активации, веса которой есть коэффициенты логистической регрессии, а вес поляризации — константа регрессионного уравнения (рис. 2).
Рис. 2 — Представление логистической регрессии в виде нейронной сети
Однослойная нейронная сеть может успешно решить лишь задачу линейной сепарации. Поэтому возможности по моделированию нелинейных зависимостей у логистической регрессии отсутствуют. Однако для оценки качества модели логистической регрессии существует эффективный инструмент ROC-анализа, что является несомненным ее преимуществом.
Для расчета коэффициентов логистической регрессии можно применять любые градиентные методы: метод сопряженных градиентов, методы переменной метрики и другие.
ROC-анализ
ROC-кривая (Receiver Operator Characteristic) — кривая, которая наиболее часто используется для представления результатов бинарной классификации в машинном обучении. Название пришло из систем обработки сигналов. Поскольку классов два, один из них называется классом с положительными исходами, второй — с отрицательными исходами. ROC-кривая показывает зависимость количества верно классифицированных положительных примеров от количества неверно классифицированных отрицательных примеров.
В терминологии ROC-анализа первые называются истинно положительным, вторые — ложно отрицательным множеством. При этом предполагается, что у классификатора имеется некоторый параметр, варьируя который, мы будем получать то или иное разбиение на два класса. Этот параметр часто называют порогом, или точкой отсечения (cut-off value). В зависимости от него будут получаться различные величины ошибок I и II рода.
В логистической регрессии порог отсечения изменяется от 0 до 1 — это и есть расчетное значение уравнения регрессии. Будем называть его рейтингом.
Для понимания сути ошибок I и II рода рассмотрим четырехпольную таблицу сопряженности (confusion matrix), которая строится на основе результатов классификации моделью и фактической (объективной) принадлежностью примеров к классам.
| Модель | Фактически положительно | Фактически отрицательно |
|---|---|---|
| Положительно | TP | FP |
| Отрицательно | FN | TN |
Что является положительным событием, а что — отрицательным, зависит от конкретной задачи. Например, если мы прогнозируем вероятность наличия заболевания, то положительным исходом будет класс «Больной пациент», отрицательным — «Здоровый пациент». И наоборот, если мы хотим определить вероятность того, что человек здоров, то положительным исходом будет класс «Здоровый пациент», и так далее.
При анализе чаще оперируют не абсолютными показателями, а относительными — долями (rates), выраженными в процентах:
Введем еще два определения: чувствительность и специфичность модели. Ими определяется объективная ценность любого бинарного классификатора.
Чувствительность (Sensitivity) — это и есть доля истинно положительных случаев:
Специфичность (Specificity) — доля истинно отрицательных случаев, которые были правильно идентифицированы моделью:
Заметим, что FPR=100-Sp
Попытаемся разобраться в этих определениях.
Модель с высокой чувствительностью часто дает истинный результат при наличии положительного исхода (обнаруживает положительные примеры). Наоборот, модель с высокой специфичностью чаще дает истинный результат при наличии отрицательного исхода (обнаруживает отрицательные примеры). Если рассуждать в терминах медицины — задачи диагностики заболевания, где модель классификации пациентов на больных и здоровых называется диагностическим тестом, то получится следующее:
ROC-кривая получается следующим образом:
Канонический алгоритм построения ROC-кривой
В результате вырисовывается некоторая кривая (рис. 3).
Для идеального классификатора график ROC-кривой проходит через верхний левый угол, где доля истинно положительных случаев составляет 100% или 1,0 (идеальная чувствительность), а доля ложно положительных примеров равна нулю. Поэтому чем ближе кривая к верхнему левому углу, тем выше предсказательная способность модели. Наоборот, чем меньше изгиб кривой и чем ближе она расположена к диагональной прямой, тем менее эффективна модель. Диагональная линия соответствует «бесполезному» классификатору, т.е. полной неразличимости двух классов.
При визуальной оценке ROC-кривых расположение их относительно друг друга указывает на их сравнительную эффективность. Кривая, расположенная выше и левее, свидетельствует о большей предсказательной способности модели. Так, на рис. 4 две ROC-кривые совмещены на одном графике. Видно, что модель «A» лучше.
Рис. 4 — Сравнение ROC-кривых
Визуальное сравнение кривых ROC не всегда позволяет выявить наиболее эффективную модель. Своеобразным методом сравнения ROC-кривых является оценка площади под кривыми. Теоретически она изменяется от 0 до 1,0, но, поскольку модель всегда характеризуются кривой, расположенной выше положительной диагонали, то обычно говорят об изменениях от 0,5 («бесполезный» классификатор) до 1,0 («идеальная» модель).
Эта оценка может быть получена непосредственно вычислением площади под многогранником, ограниченным справа и снизу осями координат и слева вверху — экспериментально полученными точками (рис. 5). Численный показатель площади под кривой называется AUC (Area Under Curve). Вычислить его можно, например, с помощью численного метода трапеций:
AUC = \int f(x)\,dx = \sum_i \Bigl[ \frac
Рис. 5 — Площадь под ROC-кривой
| Интервал AUC | Качество модели |
|---|---|
| 0,9-1,0 | Отличное |
| 0,8-0,9 | Очень хорошее |
| 0,7-0,8 | Хорошее |
| 0,6-0,7 | Среднее |
| 0,5-0,6 | Неудовлетворительное |
Порог отсечения нужен для того, чтобы применять модель на практике: относить новые примеры к одному из двух классов. Для определения оптимального порога нужно задать критерий его определения, т.к. в разных задачах присутствует своя оптимальная стратегия. Критериями выбора порога отсечения могут выступать:
Второе значение порога обычно предлагается пользователю по умолчанию. В третьем случае порог есть точка пересечения двух кривых, когда по оси X откладывается порог отсечения, а по оси Y — чувствительность или специфичность модели (рис. 6).
Рис. 6 — «Точка баланса» между чувствительностью и специфичностью
Существуют и другие подходы, когда ошибкам I и II рода назначается вес, который интерпретируется как цена ошибок. Но здесь встает проблема определения этих весов, что само по себе является сложной, а часто не разрешимой задачей.