луна в зените что это
Почему Луна над горизонтом кажется больше?
 |
 |
Иллюзия Луны — оптическая иллюзия, которая заключается в том, что Луна низко над горизонтом кажется в несколько раз больше, чем когда она находится высоко в небе (около зенита). На самом деле угловой размер Луны практически не зависит от её высоты над горизонтом. Иллюзия возникает и при наблюдениях Солнца и созвездий. Свидетельства о феномене сохранились с древних времён и зафиксированы в различных источниках человеческой культуры. В настоящее время существует несколько различных теорий, объясняющих эту иллюзию.
Широко распространено заблуждение, бытующее как минимум со времён Аристотеля (IV век до н. э.), заключающееся в том, что бо́льший размер Луны у горизонта объясняется увеличением, создаваемым атмосферой Земли. На самом деле астрономическая рефракция у горизонта, наоборот, немного уменьшает наблюдаемый размер Луны по вертикали и не влияет на размер по горизонтали. В результате лунный диск около горизонта виден приплюснутым.
Есть и ещё один фактор, из-за которого угловой размер Луны около горизонта слегка меньше, чем когда она в зените. С перемещением Луны от зенита к горизонту расстояние от неё до наблюдателя возрастает на величину земного радиуса, и её видимый размер уменьшается на 1,7 %.
Кроме того, угловой размер Луны слегка меняется в зависимости от её положения на орбите. Поскольку её орбита заметно вытянута, в перигее (ближайшей к Земле точке орбиты) угловой размер Луны составляет 33,5 угловых минут, а в апогее — на 12 % меньше (29,43 угловых минут)[1][2]. Эти незначительные изменения не связаны с кажущимся многократным увеличением Луны у горизонта: оно представляет собой ошибку восприятия. Измерения с помощью теодолита и фотографии Луны на различной высоте над горизонтом показывают неизменность размера, около половины градуса, а проекция лунного диска на сетчатку невооружённого глаза наблюдателя всегда имеет размер около 0,15 мм.
 |
Самый простой способ продемонстрировать иллюзорность эффекта — это подержать небольшой объект (например, монетку) на вытянутой руке, прикрыв при этом один глаз. Сравнивая размер объекта с большой Луной у горизонта и с маленькой Луной высоко в небе, можно увидеть, что относительный размер не изменяется. Можно также сделать из листа бумаги трубу и смотреть через неё только на Луну, без окружающих объектов — иллюзия исчезнет.
Размер видимого нами объекта может быть определён либо через его угловой размер (угол, который образуют входящие в глаз лучи от краёв объекта) либо через его физический размер (реальный размер, например в метрах). Эти два понятия различаются с точки зрения человеческого восприятия. Например, угловые размеры двух одинаковых объектов, помещённых на расстоянии 5 и 10 метров от наблюдателя, различаются почти в два раза, однако, нам, как правило, не кажется, что ближний объект в два раза больше. И наоборот, если более удалённый объект имеет тот же угловой размер, что и более близкий, мы будем его воспринимать как в два раза больший (закон Эммерта).
На данный момент не достигнуто согласия по вопросу, из-за чего Луна кажется больше у горизонта — из-за бо́льшего воспринимаемого углового размера или из-за бо́льшего воспринимаемого физического размера, то есть кажется ли она как находящаяся ближе или как увеличившаяся в размере.
Вообще, полного объяснения этой особенности человеческого восприятия до сих пор не существует. В 2002 году Хелен Росс и Корнелис Плаг выпустили книгу «Загадка лунной иллюзии»[3], в которой, рассмотрев различные теории, сделали вывод: «Ни одна теория не победила». К тому же решению пришли авторы сборника «Лунная иллюзия», выпущенного в 1989 году под редакцией М. Хершенсона[4].
Существует много различных теорий, объясняющих иллюзию Луны. Ниже перечислены лишь основные из них.
В 1940-х годах Боринг (Boring, 1943; Holway & Boring, 1940; Taylor & Boring, 1942) и в 1990-х Судзуки (Suzuki, 1991,1998) предложили объяснение иллюзии Луны, согласно которому, кажущаяся величина Луны зависит от степени конвергенции глаз наблюдателя. То есть иллюзия Луны — это результат усиления импульсов к конвергенции глаз, возникающих у наблюдателя, когда он поднимает взгляд наверх (чтобы посмотреть на Луну в зените), а глаза сами по себе стремятся дивергировать. Из-за того, что конвергенция глаз является одним из признаков близости объекта, наблюдателю кажется, что объект высоко в небе меньше по размеру.
В одном из экспериментов Холуэй и Боринг (Holway & Boring, 1940) просили испытуемых сравнить воспринимаемую ими величину Луны с одним из световых дисков, спроецированных на расположенный рядом с ними экран. В первой серии эксперимента испытуемые сидели на стуле. Наблюдая за Луной, находящейся близ горизонта (на уровне глаз наблюдателя), они выбирали диск, который значительно превосходил по величине тот, который они выбирали, когда наблюдали за Луной, находящейся в зените (подняв глаза под углом 30°). Во второй серии испытуемые наблюдали за Луной лёжа на столе. Когда они лежали на спине и смотрели на Луну в зените или когда они были вынуждены закидывать голову назад и поднимать глаза вверх, чтобы из положения на спине увидеть Луну на горизонте, результаты были противоположными. Луна близ горизонта казалась им меньше по величине, чем Луна в зените.
Противники данной гипотезы утверждают, что иллюзия увеличенной Луны быстро затухает при увеличении высоты светила над горизонтом, когда необходимость запрокидывать голову и поднимать глаза вверх ещё не возникает.
По теории относительного размера воспринимаемый размер зависит не только от размера на сетчатке, но и от размеров остальных объектов в поле зрения, которые мы наблюдаем одновременно. При наблюдении Луны близко к горизонту мы видим не только Луну, но и другие объекты, на фоне которых спутник Земли кажется больше, чем есть на самом деле. Когда же Луна находится в небе, бескрайние просторы неба заставляют её выглядеть меньше.
Данный эффект был продемонстрирован психологом Германом Эббингаузом. Круг, окружённый маленькими кругами, представляет собой Луну у горизонта и окружающие её маленькие объекты (деревья, столбы и т. п.), а круг, окружённый более крупными объектами, представляет собой Луну в небе. При том, что оба центральных круга имеют одинаковый размер, многим людям кажется, что правый круг на картинке больше. Этот эффект может проверить каждый, вынеся из комнаты во двор какой-нибудь крупный предмет (например, стол). На открытом пространстве он будет выглядеть явно меньше, чем в помещении.
Противники данной теории указывают на то, что пилоты самолётов тоже наблюдают данную иллюзию, хотя в их поле зрения наземных объектов нет.
Теория кажущейся удалённости впервые была описана у Клеомеда примерно в 200 г. н. э. Теория предполагает, что Луна у горизонта выглядит больше Луны в небе из-за того, что она кажется дальше. Мозг человека видит небо не как полусферу, чем оно на самом деле является, а как сплюснутый купол. Наблюдая за облаками, птицами и самолётами, человек видит, что они уменьшаются при приближении к горизонту. В отличие от земных объектов, Луна, находясь вблизи горизонта, имеет примерно такой же видимый угловой диаметр, как и в зените, но человеческий мозг пытается компенсировать перспективные искажения и предполагает, что диск Луны должен быть физически больше.
 |
 |
Эксперименты, проведённые в 1962 году Кауфманом и Роком (Kaufman & Rock)[5], показали, что существенным фактором при создании иллюзии являются наглядные ориентиры.
Луна у горизонта оказывается в конце последовательности объектов ландшафта, деревьев и зданий, что говорит мозгу о её большой удалённости. При удалении ориентиров из поля зрения, выглядящая крупной Луна становится меньше.
Такое же объяснение предлагают Джозеф Антонидес (Joseph Antonides) и Тоширо Кубота (Toshiro Kubota) из Университета Саскуэханны (США) в недавно опубликованной работе[6]. Да, механизм контрастно-размерной теории проверен в иллюзии Эббингауза. Но типичный размер кажущегося увеличения предметов в такой иллюзии равен 10%. А кажущееся увеличение Луны у горизонта равно двукратному (при предельно нижнем положении, не во всех широтах). Самое интересное, отмечают они, что иллюзия Эббингазуа, как и большинство оптических иллюзий вообще, не исчезает на фото. Луна же на фотографии вовсе не кажется большей, чем на самом деле.
Исследователи обращаются к модной теории, гласящей о том, что информация, попадающая в зрительную кору головного мозга, идёт в ней двумя разными потоками. Первый — это бинокулярное зрение. Когда изображение от обоих глаз одинаково, объект должен быть далеко, и чем выше сходство изображений, получаемых обоими глазами, тем дальше он находится.
Второй путь использует встроенную в наше восприятие модель мира. В ней мы интуитивно воспринимаем небо как находящееся на некоторой конечной дистанции от нас, а Солнце и Луну (как и звёзды) — располагающимися перед небом (относительно нас), при этом небо служит им фоном.
В отношении небесных объектов это порождает противоречие. Бинокулярное зрение не обманывает — Луна и в самом деле дальше от нас, нежели небо, причём эта разница достигает сотен раз.
 |
Однако мозг не может работать на основании столь отличающихся данных, противоречие надо исключить. Поэтому он искажает проекцию Луны, посредством преувеличения различий в картинке, поступающей от одного и другого глаза, а именно такие различия выступают мерилом дальности объекта. Степень же искажения зависит от кажущейся дистанции до небосвода. У земли, где на его фоне видны деревья и другие предметы, небо кажется ближе, что уменьшает противоречие между двумя каналами получения информации. Поэтому у горизонта искажение минимизируется, и мозг позволяет глазам увидеть объект бóльшим.
Как проверить идею? Г-да Антонидес и Кубота хотят измерить изменения кажущегося размера Луны с разными «подсказчиками» в открытом поле, долине, в горах, городском ландшафте и так далее. Кроме того, небезынтересно было бы выяснить и то, существует ли иллюзия у людей с отсутствием бинокулярного зрения. Также они намерены исследовать вопрос о точности сообщений, говорящих, что иллюзия исчезает, если мы смотрим на Луну у горизонта вверх ногами, стоя на голове.
Противники данной теории указывают на наличие иллюзии даже при наблюдении светила через темный светофильтр, когда окружающие его объекты неразличимы.
Луна в зените что это
9. Луна в зените
А Когда угловой диаметр Луны больше: когда она находится вблизи зенита или вблизи горизонта?
Б Вообще Луна у горизонта выглядит более крупной, чем на большой высоте. Но мы знаем, что это оптический обман. Ведь Луна и в зените, и на горизонте одна и та же. Более того, в тот момент, когда мы видим ее большой на горизонте, где-то кто-то другой видит ее маленькой в зените. Не может же она одновременно быть и большой, и маленькой!
Таков ответ большинства читателей, и в нем все логично, кроме последней фразы. По мнению автора, угловые размеры Луны у горизонта в действительности меньше, чем у зенита. А как думаете вы?
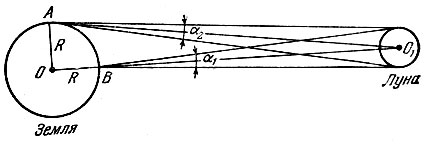
В Угловые размеры Луны определяются ее линейными размерами М и расстоянием до наблюдателя. Пусть в данный момент расстояние между центрами Земли и Луны 380 000 км (в силу эллиптичности орбиты Луны это расстояние меняется в пределах между 363 300 и 405 500 км). Тогда от наблюдателя А (рис. 6), видящего Луну у самого горизонта, расстояние до Луны тоже равно приблизительно 380 000 км (AO1 ≈ OO1). Однако наблюдатель В, видящий Луну в зените, находится ближе к ней приблизительно на величину радиуса земного шара R ≈ 6380 км:
Следовательно, угловые размеры Луны для наблюдателя В больше, чем для наблюдателя А (α1 > α2), приблизительно во столько раз, во сколько ВО1 меньше АО1 т. е. на 1,7%.
Рис. 6
Отметим, что в наших широтах увидеть Луну в зените, нельзя. Солнце в зените может увидеть наблюдатель в широтах ± 23,5° (угол наклона плоскости эклиптики к плоскости экватора). Поскольку плоскость орбиты Луны наклонена к плоскости эклиптики приблизительно на 5°, то Луну в зените можно увидеть в широтах ± 28,5°.
На широте Ленинграда Луна иногда поднимается на 58,5° над горизонтом. Этого вполне достаточно для проявления как субъективного эффекта уменьшения диаметра Луны с высотой, так и объективного обратного эффекта.
Рефракция, приводящая к заметному сжатию вертикального диаметра Луны, находящейся очень близко к горизонту, дополнительно усиливает эффект, рассмотренный в задаче.
Занимательная астрономия — факты о Луне
Интересности
Все знают что Луна обращена к Земле всегда одной стороной, но мало кто знает что благодаря либрации суммарно можно наблюдать около 59 % лунной поверхности. Данное явление было открыто Галилео Галилеем в 1635 году, когда он был осуждён Инквизицией.
Об этом и многом другом читаем под катом.
Вращение системы Земля-Луна происходит не вокруг центра Земли, а вокруг центра масс системы Земля-Луна, который находится на расстоянии 1700 км под поверхностью Земли.
Лунные день и ночь длятся по 14,8 земных суток.
Небо Луны всегда черное, даже днем, так как в нем не рассеиваются лучи Солнца.
Диск Земли выглядит с Луны в 3,67 раз больше, чем Луна с Земли и висит практически неподвижно.
Солнце притягивает Луну в 2,2 раза сильнее чем Земля.
Полная Луна отражает только 7 % падающего на неё солнечного света.
Освещение отражённым светом Земли примерно в 50 раз сильнее, чем освещение лунным светом на Земле.
Свет, пущенный с Земли, достигает Луны за 1,28 секунды
Из-за приливной синхронизации Луна всегда обращена к Земле одной стороной, а орбита ее представляет собой медленно раскручивающуюся спираль — Луна постепенно удаляется от Земли со скоростью примерно 38 мм/год.
Через миллионы лет это крошечное изменение, а также увеличение земного дня на 23 мкс в год, приведут к значительным изменениям. Так, например, в Девонский период (примерно 410 млн лет назад) в году было 400 дней, а сутки длились 21,8 часа.
Максимальная амплитуда приливной волны на Земле наблюдается в заливе Фанди в Канаде и составляет 18 метров.
Приливообразующая сила Солнца в среднем в 2,17 раза меньше лунной.
Луна — восемнадцатая карта (аркан) Таро.
Во время лунного затмения (даже полного) Луна не исчезает полностью, а становится тёмно-красной. Это связано с тем, что земная атмосфера лучше всего пропускает через себя оттенки красного цвета что отчетливо видно во время заката или рассвета. Именно этот рассеянный «закатный» цвет и освещает Луну во время затмения.
Иллюзия Луны («лунная иллюзия») — оптическая иллюзия, при которой воспринимаемый размер Луны примерно в полтора раза больше, когда она находится низко над горизонтом, по сравнению с тем, как она воспринимается при нахождении высоко в небе (в зените), хотя её проекции на сетчатку глаза в обоих случаях равны между собой.
Когда человек смотрит на Луну, лучи лунного света формируют на его сетчатке изображение размером около 0,15 мм.
С Земли видимый размер Луны очень близок к видимому размеру Солнца. Угловые размеры (или телесный угол) этих двух небесных тел схожи постольку, поскольку хоть диаметр Солнца и больше лунного в 400 раз, оно находится в 400 раз дальше от Земли.
Лунная радуга (также известная как ночная радуга) — радуга, порождаемая луной в большей степени, чем Солнцем. Лунная радуга сравнительно более бледная, чем обычная. Это объясняется тем, что Луна производит (отражает от Солнца) меньше света, чем Солнце. Лунная радуга всегда находится на противоположной от Луны стороне неба.
Наиболее распространённая теория происхождения Луны, Теория гигантского столкновения, утверждает, что Луна образовалась в результате столкновения протопланеты Теи (размером примерно с Марс) с ранней Землёй. Эта гипотеза, среди прочего, объясняет причины сходства и различия состава лунного грунта и земного.
Подготовлено по материалам Википедии и других научно-познавательных сайтах о Луне в частности и астрономии в целом.
Задача 9. Луна в зените
Пётр Маковецкий. Смотри в корень! Сборник любопытных задач и вопросов
Когда угловой диаметр Луны больше: когда она находится вблизи зенита или вблизи горизонта?
Вообще Луна у горизонта выглядит более крупной, чем на большой высоте. Но мы знаем, что это оптический обман. Ведь Луна и в зените, и на горизонте одна и та же. Более того, в тот момент, когда мы видим ее большой на горизонте, где-то кто-то другой видит ее маленькой в зените. Не может же она одновременно быть и большой, и маленькой.
Таков ответ большинства читателей, и в нем все логично, кроме последней фразы. По мнению автора, угловые размеры Луны у горизонта в действительности меньше, чем у зенита. А как думаете вы?
Угловые размеры Луны определяются ее линейными размерами и расстоянием до наблюдателя. Пусть в данный момент расстояние между центрами Земли и Луны 380 000 км (в силу эллиптичности орбиты Луны это расстояние меняется в пределах между 363 300 и 405 500 км). Тогда от наблюдателя A (рис. 6), видящего Луну у самого горизонта, расстояние до Луны тоже равно приблизительно 380 000 км (AO1 ≈ OO1). Однако наблюдатель B, видящий Луну в зените, находится ближе к ней приблизительно на величину радиуса земного шара R ≈ 6380 км:
Следовательно, угловые размеры Луны для наблюдателя B больше, чем для наблюдателя A (α1 > α2), приблизительно во столько раз, во сколько BO1 меньше AO1, т.е. на 1,7%.
Разумеется, все эти расчеты верны лишь в пределах одного дня. Эллиптичность орбиты Луны может привести к тому, что для одного и того же наблюдателя Луна в зените сегодня будет меньше Луны у горизонта две недели назад. Однако за время перехода Луны от горизонта к зениту (порядка четверти суток) расстояние Земля – Луна меняется меньше, чем на радиус Земли.
Отметим, что в наших широтах увидеть Луну в зените нельзя. Солнце в зените может увидеть наблюдатель в широтах ±23,5° (угол наклона плоскости эклиптики к плоскости экватора). Поскольку плоскость орбиты Луны наклонена к плоскости эклиптики приблизительно на 5°, то Луну в зените можно увидеть в широтах ±28,5°.
На широте Ленинграда Луна иногда поднимается на 58,5° над горизонтом. Этого вполне достаточно для проявления как субъективного эффекта уменьшения диаметра Луны с высотой, так и объективного обратного эффекта.
Рефракция, приводящая к заметному сжатию вертикального диаметра Луны, находящейся очень близко к горизонту, дополнительно усиливает эффект, рассмотренный в задаче.
Логические задачи и головоломки
Когда угловой диаметр Луны больше: когда она находится вблизи зенита или вблизи горизонта?
Ответ: Вообще Луна у горизонта выглядит более крупной, чем на большой высоте. Но мы знаем, что это оптический обман. Ведь Луна и в зените, и на горизонте одна и та же. Более того, в тот момент, когда мы видим ее большой на горизонте, где-то кто-то другой видит ее маленькой в зените. Не может же она одновременно быть и большой, и маленькой.
Таков ответ большинства читателей, и в нем все логично, кроме последней фразы. По мнению автора, угловые размеры Луны у горизонта в действительности меньше, чем у зенита. А как думаете вы?
В.
Угловые размеры Луны определяются ее линейными размерами и расстоянием до наблюдателя. Пусть в данный момент расстояние между центрами Земли и Луны 380 000 км (в силу эллиптичности орбиты Луны это расстояние меняется в пределах между 363 300 и 405 500 км). Тогда от наблюдателя A (рис. 6), видящего Луну у самого горизонта, расстояние до Луны тоже равно приблизительно 380 000 км (AO1 ≈ OO1). Однако наблюдатель B, видящий Луну в зените, находится ближе к ней приблизительно на величину радиуса земного шара R ≈ 6380 км:
BO1 = OO1 – OB = 380 000 – 6 380 = 373 620 км.
Следовательно, угловые размеры Луны для наблюдателя B больше, чем для наблюдателя A (α1 > α2), приблизительно во столько раз, во сколько BO1 меньше AO1, т.е. на 1,7%.
Разумеется, все эти расчеты верны лишь в пределах одного дня. Эллиптичность орбиты Луны может привести к тому, что для одного и того же наблюдателя Луна в зените сегодня будет меньше Луны у горизонта две недели назад. Однако за время перехода Луны от горизонта к зениту (порядка четверти суток) расстояние Земля – Луна меняется меньше, чем на радиус Земли.
Отметим, что в наших широтах увидеть Луну в зените нельзя. Солнце в зените может увидеть наблюдатель в широтах ±23,5° (угол наклона плоскости эклиптики к плоскости экватора). Поскольку плоскость орбиты Луны наклонена к плоскости эклиптики приблизительно на 5°, то Луну в зените можно увидеть в широтах ±28,5°.
На широте Ленинграда Луна иногда поднимается на 58,5° над горизонтом. Этого вполне достаточно для проявления как субъективного эффекта уменьшения диаметра Луны с высотой, так и объективного обратного эффекта.
Рефракция, приводящая к заметному сжатию вертикального диаметра Луны, находящейся очень близко к горизонту, дополнительно усиливает эффект, рассмотренный в задаче.