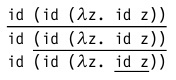лямбда что за алфавит
Что такое лямбда? 11-я буква греческого алфавита
В настоящее время древнегреческий язык утратил многие признаки категории живого языка. Однако до сих пор на страницах школьных учебников, монастырских и церковных книг можно обнаружить древнегреческие слова и символы, используемые в качестве обозначения определенных величин.
За время своего существования древнегреческий язык сыграл большую роль в развитии мировой письменности и предопределил развитие некоторых мировых языков.
Интерес к языку подпитывается нередкими исследованиями алфавита, правил правописания и произношения. В данной статье узнаем, что представляет собой 11-я буква греческого алфавита – лямбда.
Наука и Греция
Алфавит, изобретенный греками, основан на финикийской и древнегреческой азбуке. Его основная особенность заключается в содержании двух типов букв – согласных и гласных. Прошло более двух десятков веков, но алфавит сохранился.
В научной среде греческий алфавит занимает прочное место. Во многих отраслях знаний его буквы можно обнаружить в качестве обозначения некоторых показателей. В математике синус угла обозначается α, используется знак суммы Σ. В астрономии в названии самых крупных звезд ярких созвездий упоминается α (альфа Большого Пса). В биологии при изучении групп особей активно используются понятия омега-самка и альфа-самец. В разделе ядерной физики можно встретиться с понятиями гамма-частицы и альфа-излучения. На страницах учебников химии и физики в качестве постоянных величин фигурируют ρ и λ, которыми обозначают плотность материала и длину волны соответственно. О последней букве расскажем подробнее, то есть ответим на вопросы о том, как пишется лямбда, откуда берет происхождение и где применяется.
Правописание
В первых версиях греческого алфавита внешний вид лямбды отличался от современного представления, хотя общее сходство наблюдалось. Большинство вариаций написания были представлены двумя прямыми линиями, одна из которых незначительно короче другой, а их концы сходятся. В восточном алфавите угол соединения находился в верхнем углу, в западном – в левом нижнем. Впоследствии римляне определились, что угол у них будет внизу слева, а греки решили, что он будет сверху. Последующий вариант содержал в себе вертикальный штрих с наклонной линией, уходящей вправо. В настоящее время букву лямбду прописную пишут согласно последнему описанному варианту, а заглавная выглядит в виде перевернутого знака V. На основе греческой лямбды образовалась латинская лямбда, заглавный символ которой представлен в виде перевернутого Y.
Значение
Лямбда образовалась от буквы финикийского алфавита – ламед. Данному символу в числовой алфавитной системе соответствовало число 30, которое в Греции приписывали справа сверху около вертикальной линии символа. На основании буквы лямбды образовались кириллическая Л и латинская L, а после и производные последних.
Использование прописной буквы
Области применения прописной версии буквы довольно обширны. Раньше символ можно было обнаружить на щитовых узорах спартанских войск. Сейчас он сохранился при обозначении вида частиц в физике, а в математике он представляет собой диагональную матрицу из собственных значений и выступает вводимыми операторами. Такое описание поясняет, что такое лямбда прописная и где она используется.
Строчная лямбда
Строчная буква λ закрепилась и занимает прочное место в физических формулах алгебры, физики, химии, информатики. Удельная теплота плавления, постоянная распада, длина волны, значение Ламе, линейная плотность электрического заряда – это те переменные, которые для простоты заменены этим символом. В биологии изучается вирус фаг лямбда. В информатике функциональные выражения производят в λ-исчислении. В самолетостроении при удлинении крыла вводится буква лямбда. В линейной алгебре найденные корни дифференциального уравнения также обозначаются через нее.
Каждый современный автомобилист знаком с лямбда-зондом, установленным в его транспортном средстве. Прибор измеряет количество образуемого углекислого газа в выхлопе. Оснащение автомобиля данным датчиком произошло по причине того, что власти многих стран заботятся об экологической составляющей и здоровье нации и таким образом регулируют количество выделяемого автомобилем СО2. В случае критичности значения этого показателя, то есть его превышения относительно допустимой величины, в качестве жесткой меры выписывается штраф. Этот датчик также необходим для соблюдения оптимального и экономного расхода топлива.
Связь с культурной сферой
Что такое лямбда в культурной среде? В известном кинофильме «Звездные войны» путешествовал космический корабль класса лямбда. Буква также используется в компьютерных играх под эмблемой «Комплекс Лямбда». По мере развития сюжета игры она применяется в качестве знака противоборства между населением и альянсом. Символ существует и в эмблеме игр, строчная буква лямбда нередко фигурирует в слове Half-Life, в итоге получается Hλlf-Life.
В романтической песне под названием «Австралия» Михаила Щербакова герой мечтал завести кенгуру, муравьеда или жирафа по имени Лямбда.
В 1970 году, когда регулярно стали проходить гей-парады, значок лямбда был впервые использован в Нью-Йорке в качестве обозначения правозащитной организации «Альянс гей-активистов». Через четыре года в Шотландии Международным конгрессом прав геев «λ» признана интернациональным знаком движения за свободу и права людей с нетрадиционной ориентацией.
В настоящее время под знаком лямбды в культуре понимают объединение именно таких людей. Активисты при объяснении, почему именно этот символ выбран ключевым для описания их движения, ссылаются на физическое понятие длины волны. Они видят аналогию с волной, направленной в пространство и бесконечность, и считают, что лямбда является удачным обозначением для описания предстоящих изменений в социуме, в котором лиц нетрадиционной ориентации должны принять.
Сакральное значение
Что такое лямбда в эзотерическом плане? Лямбда заключает в себе принцип органического роста и переход системы на возвышенный уровень. Это подтверждается примерами двух видов прогрессий, ключевых числовых последовательностей древнегреческой математики, где используется знак. В теоретическом плане буква символизирует возрастание числовых рядов, которыми описывается любая система физических явлений. Каждый, рассматривая руны, обозначающие возвышение и означающие звук «Л» или древнееврейский знак ламед, обнаружит сходство с исследуемой буквой.
В данной статье было рассмотрено, что такое лямбда, и где ее можно встретить в окружающем мире.
Λ Греческая заглавная буква лямбда
U+039B
Нажмите, чтобы скопировать и вставить символ
Техническая информация
Значение символа
Греческая заглавная буква лямбда. Греческое и коптское письмо.
Символ «Греческая заглавная буква лямбда» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Греческое и коптское письмо |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 03BB |
| Простое изменение регистра | 03BB |
Похожие символы
Греческая заглавная буква альфа
Греческая заглавная буква омикрон
Греческая строчная буква лямбда
Греческая заглавная буква бета
Греческая заглавная буква омега
Греческая заглавная буква пси
Греческая заглавная буква хи
Греческая заглавная буква фи
Греческая заглавная буква ипсилон
Греческая заглавная буква сигма
Греческая заглавная буква ро
Греческая заглавная буква пи
Греческая заглавная буква тау
Греческая заглавная буква кси
Греческая заглавная буква эта
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | CE 9B | 206 155 | 52891 | 11001110 10011011 |
| UTF-16BE | 03 9B | 3 155 | 923 | 00000011 10011011 |
| UTF-16LE | 9B 03 | 155 3 | 39683 | 10011011 00000011 |
| UTF-32BE | 00 00 03 9B | 0 0 3 155 | 923 | 00000000 00000000 00000011 10011011 |
| UTF-32LE | 9B 03 00 00 | 155 3 0 0 | 2600665088 | 10011011 00000011 00000000 00000000 |
Наборы с этим символом:
© Таблица символов Юникода, 2012–2021.
Юникод® — это зарегистрированная торговая марка консорциума Юникод в США и других странах. Этот сайт никак не связан с консорциумом Юникод. Официальный сайт Юникода располагается по адресу www.unicode.org.
Мы используем 🍪cookie, чтобы сделать сайт максимально удобным для вас. Подробнее
λ-исчисление. Часть первая: история и теория
Идею, короткий план и ссылки на основные источники для этой статьи мне подал хабраюзер z6Dabrata, за что ему огромнейшее спасибо.
UPD: в текст внесены некоторые изменения с целью сделать его более понятным. Смысловая составляющая осталась прежней.
Вступление
Возможно, у этой системы найдутся приложения не только
в роли логического исчисления. (Алонзо Чёрч, 1932)
Вообще говоря, лямбда-исчисление не относится к предметам, которые «должен знать каждый уважающий себя программист». Это такая теоретическая штука, изучение которой необходимо, когда вы собираетесь заняться исследованием систем типов или хотите создать свой функциональный язык программирования. Тем не менее, если у вас есть желание разобраться в том, что лежит в основе Haskell, ML и им подобных, «сдвинуть точку сборки» на написание кода или просто расширить свой кругозор, то прошу под кат.
Начнём мы с традиционного (но краткого) экскурса в историю. В 30-х годах прошлого века перед математиками встала так называемая проблема разрешения (Entscheidungsproblem), сформулированная Давидом Гильбертом. Суть её в том, что вот есть у нас некий формальный язык, на котором можно написать какое-либо утверждение. Существует ли алгоритм, за конечное число шагов определяющий его истинность или ложность? Ответ был найден двумя великими учёными того времени Алонзо Чёрчем и Аланом Тьюрингом. Они показали (первый — с помощью изобретённого им λ-исчисления, а второй — теории машины Тьюринга), что для арифметики такого алгоритма не существует в принципе, т.е. Entscheidungsproblem в общем случае неразрешима.
Так лямбда-исчисление впервые громко заявило о себе, но ещё пару десятков лет продолжало быть достоянием математической логики. Пока в середине 60-х Питер Ландин не отметил, что сложный язык программирования проще изучать, сформулировав его ядро в виде небольшого базового исчисления, выражающего самые существенные механизмы языка и дополненного набором удобных производных форм, поведение которых можно выразить путем перевода на язык базового исчисления. В качестве такой основы Ландин использовал лямбда-исчисление Чёрча. И всё заверте…
λ-исчисление: основные понятия
Синтаксис
В основе лямбда-исчисления лежит понятие, известное ныне каждому программисту, — анонимная функция. В нём нет встроенных констант, элементарных операторов, чисел, арифметических операций, условных выражений, циклов и т. п. — только функции, только хардкор. Потому что лямбда-исчисление — это не язык программирования, а формальный аппарат, способный определить в своих терминах любую языковую конструкцию или алгоритм. В этом смысле оно созвучно машине Тьюринга, только соответствует функциональной парадигме, а не императивной.
Мы с вами рассмотрим его наиболее простую форму: чистое нетипизированное лямбда-исчисление, и вот что конкретно будет в нашем распоряжении.
Процесс вычисления
Рассмотрим следующий терм-применение:
Существует несколько стратегий выбора редекса для очередного шага вычисления. Рассматривать их мы будем на примере следующего терма:
который для простоты можно переписать как
(напомним, что id — это функция тождества вида λx.x )
В этом терме содержится три редекса:
Недостатком стратегии вызова по значению является то, что она может зациклиться и не найти существующее нормальное значение терма. Рассмотрим для примера выражение
(λx.λy. x) z ((λx.x x)(λx.x x))
Этот терм имеет нормальную форму z несмотря на то, что его второй аргумент такой формой не обладает. На её-то вычислении и зависнет стратегия вызова по значению, в то время как стратегия вызова по имени начнёт с самого внешнего терма и там определит, что второй аргумент не нужен в принципе. Вывод: если у редекса есть нормальная форма, то «ленивая» стратегия её обязательно найдёт.
На этом закончим вводную в лямбда-исчисление. В следующей статье мы займёмся тем, ради чего всё и затевалось: программированием на λ-исчислении.
Лямбда выражения — ликбез
Лямбда выражения — довольно тривиальная штука. Это выражение, составленное из переменных, объединенных операциями применения и абстракции. Что это за операции? Очень просто.
Абстракция.
Записывается так:
λx.y
где x — переменная, y — это произвольное лямбда выражение, а λ и точечка — это просто обозначение операции абстракции. Семантика у этого простая — это выражение представляет собой функцию от одной переменной x, тело которой определяется выражением y (в котором может присутствовать переменная x, естественно).
Если кому-то знаком C#, то это можно мыслить себе как аналог выражения x => y.
Применение.
Записывается так:
x y
где x и y — это произвольные лямбда-выражения. Семантика — вызов функции x со значением y в качестве аргумента. На C# аналог «x(y)». В лямбда выражении эти сишарповые скобочки можно не ставить (а можно и ставить, но об этом следующий абзац).
Плюс ко всему можно ставить скобки, чтобы разрешить неоднозначности:
Например по выражению λx.x y z сразу и не скажешь, что это (λx. x) (y z) или ((λx. x) y) z или (λx.(x y)) z или λx.(x (y z)) или может быть λx.(x (y z)).
Чтобы не ставить много скобок, у операций определены приоритеты и ассоциативность, согласно которым λx.x y z следует всегда интерпретировать как λx.((x y) z), но это нужно исключительно для удобства.
Теперь самое важное. С лямбда выражением можно ассоциировать понятие «вычисления выражения».
Вычисляется оно посредством последовательных редукций до тех пор, пока не окажется, что редуцировать больше нечего.
Можно считать, что редукция — это замена терма (λx.y) z на терм y[x := z]. То есть на терм y, в котором все не связанные вхождения x заменены на z.Что такое связанные вхождения? В выражении λx.y все вхождения переменной x внутри y — связанные. Другими словами связанные вхождения переменных — это формальные параметры функции. Таким образом y[x := z] — это замена всех переменных x, не являющихся формальными аргументами в y на выражение z. Пример замены должен окончательно все прояснить:
((λy.λx.x) x)[x := z] = (λy.λx.x) z.
Вообще-то в умных книжках можно встретить гораздо более общее понятие термина «редукция», но оставлю это вам для самостоятельного изучения. 😉
В конце процесса редукции (если он заканчивается), получается нормальная форма. То есть выражение, которое больше никак нельзя редуцировать.
Доказано, что нормальная форма единственна, если она, конечно, вообще существует (а иногда она не существует, что можно себе мыслить, как функцию с вечным циклом или с бесконечной рекурсией).
В этом примере редуцировалось всегда самое левое из самых внешних подвыражений. Такой порядок редукции называется нормальным. Видно, что он даже и не взялся за вычисление подвыражения ((λx.x) B), потому что от него результат не зависит. Такое поведение называют «ленивым вычислением». Это одна из фич некоторых (но не всех, конечно же) функциональных языков.
Лямбда-исчисление
Лямбда-исчисление (англ. lambda calculus) — формальная система, придуманная в 1930-х годах Алонзо Чёрчем. Лямбда-функция является, по сути, анонимной функцией. Эта концепция показала себя удобной и сейчас активно используется во многих языках программирования.
Содержание
Лямбда-исчисление [ править ]
| Определение: |
| Лямбда-выражением (англ. [math]\lambda[/math] -term) называется выражение, удовлетворяющее следующей грамматике: |
Пробел во втором правиле является терминалом грамматики. Иногда его обозначают как @, чтобы он не сливался с другими символами в выражении.
В первом случае функция является просто переменной. Во втором происходит аппликация (применение) одной функции к другой. Это аналогично вычислению функции-левого операнда на аргументе-правом операнде. В третьем — абстракция по переменной. В данном случае происходит создание функции одного аргумента с заданными именем аргумента и телом функции.
[math] x\\ (x\ z)\\ (\lambda x.(x\ z))\\ (\lambda z.(\lambda w.((\lambda y.((\lambda x.(x\ z))\ y))\ w)))\\ [/math]
Приоритет операций [ править ]
Свободные и связанные переменные [ править ]
Связанными переменными называются все переменные, по которым выше в дереве разбора были абстракции. Все остальные переменные называются свободными.
Связанные переменные — это аргументы функции. То есть для функции они являются локальными.
α-эквивалетность [ править ]
и замкнуто относительно следующих правил:
[math] P=_\alpha P’ \Rightarrow \forall x \in V: \lambda x.P=_\alpha \lambda x.P’\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : P Z =_\alpha P’Z\\ P=_\alpha P’ \Rightarrow \forall Z \in \Lambda : Z P =_\alpha Z P’\\ P=_\alpha P’ \Rightarrow P’=_\alpha P\\ P=_\alpha P’ \ \& \ P’=_\alpha P» \Rightarrow P=_\alpha P»\\[/math]
β-редукция [ править ]
и замкнуто относительно следующих правил
[math]P\to _\beta P’ \Rightarrow \forall x\in V:\lambda x.P\to _\beta \lambda x.P’\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : P\ Z\to _\beta P’\ Z\\ P\to _\beta P’ \Rightarrow \forall Z\in \Lambda : Z\ P\to _\beta Z\ P'[/math]
Каррирование [ править ]
Нотация Де Брауна [ править ]
Грамматику нотации можно задать как:
Примеры выражений в этой нотации:
Переменная называется свободной, если ей соответствует число, которое больше количества абстракций на пути до неё в дереве разбора.
Определение [ править ]
Введём на основе лямбда-исчисления аналог натуральных чисел, основанный на идее, что натуральное число — это или ноль, или увеличенное на единицу натуральное число.
+1 [ править ]
Сложение [ править ]
Сложение двух чисел похоже на прибавление единицы. Но только надо прибавить не единицу, а второе число.
[math]n[/math] раз применить [math]s[/math] к применённому [math]m[/math] раз [math]s[/math] к [math]z[/math]
[math](\operatorname
[math](\operatorname
Умножение [ править ]
[math](\operatorname
Возведение в степень [ править ]
It’s a kind of magic
[math](\operatorname
Логические значения [ править ]
Стандартные функции булевой логики:
Ещё одной важной функцией является функция проверки, является ли число нулём:
Пара [ править ]
Вычитание [ править ]
В отличие от всех предыдущих функций, вычитание для натуральных чисел определено только в случае, если уменьшаемое больше вычитаемого. Положим в противном случае результат равным нулю. Пусть уже есть функция, которая вычитает из числа единицу. Тогда на её основе легко сделать, собственно, вычитание.
Если вы ничего не поняли, не огорчайтесь. Вычитание придумал Клини, когда ему вырывали зуб мудрости. А сейчас наркоз уже не тот.
Сравнение [ править ]
Комбинатор неподвижной точки [ править ]
Попробуем выразить в лямбда-исчислении какую-нибудь функцию, использующую рекурсию. Например, факториал.
Лямбда исчисление обладаем замечательным свойством: у каждой функции есть неподвижная точка!
Рассмотрим следующую функцию.
[math]\operatorname
[math]Y\ = \ \lambda f.(\lambda x.f(x\ x))\ (\lambda x.f(x\ x))[/math]
Деление [ править ]
Воспользовавшись идеей о том, что можно делать рекурсивные функции, сделаем функцию, которая будет искать частное двух чисел.
[math]\operatorname
И остатка от деления
[math]\operatorname
Проверка на простоту [ править ]
[math]\operatorname
Следующее простое число. [math]\operatorname
[math]\operatorname
[math]\operatorname
Списки [ править ]
Для работы со списками чисел нам понадобятся следующие функции:
[math]\operatorname
[math]\operatorname
Выводы [ править ]
На основе этого всего уже можно реализовать эмулятор машины тьюринга: с помощью пар, списков чисел можно хранить состояния. С помощью рекурсии можно обрабатывать переходы. Входная строка будет даваться, например, закодированной аналогично списку: пара из длины и числа, характеризующего список степенями простых. Я бы продолжил это писать, но уже на операции [math]\operatorname
[1, 2][/math] я не дождался окончания выполнения. Скорость лямбда-исчисления как вычислителя печальна.