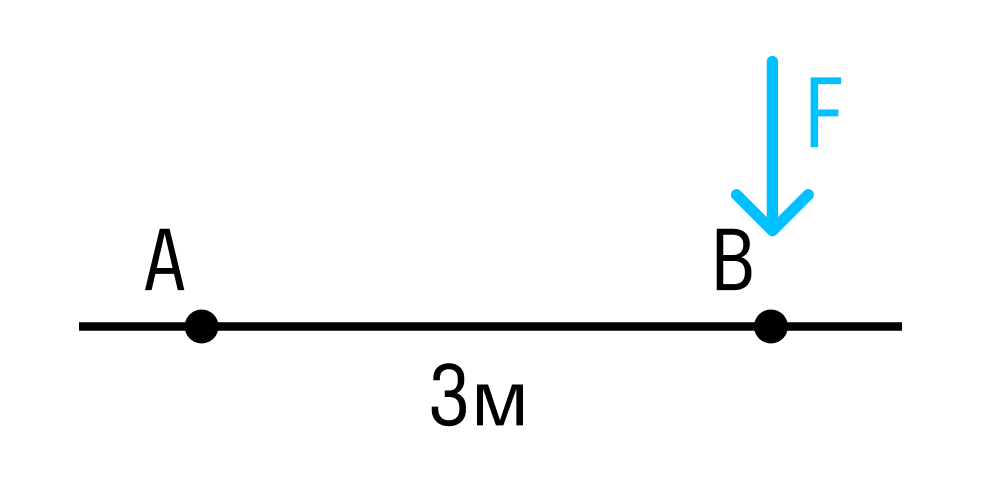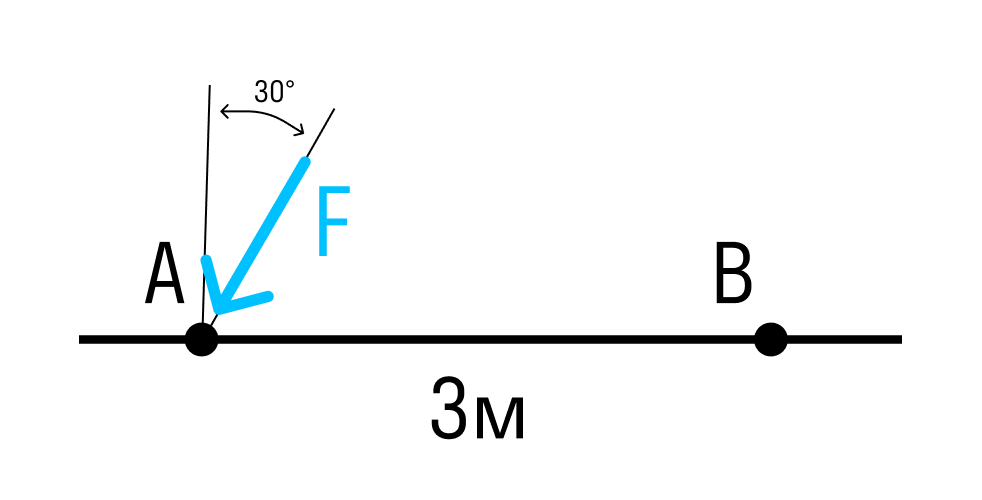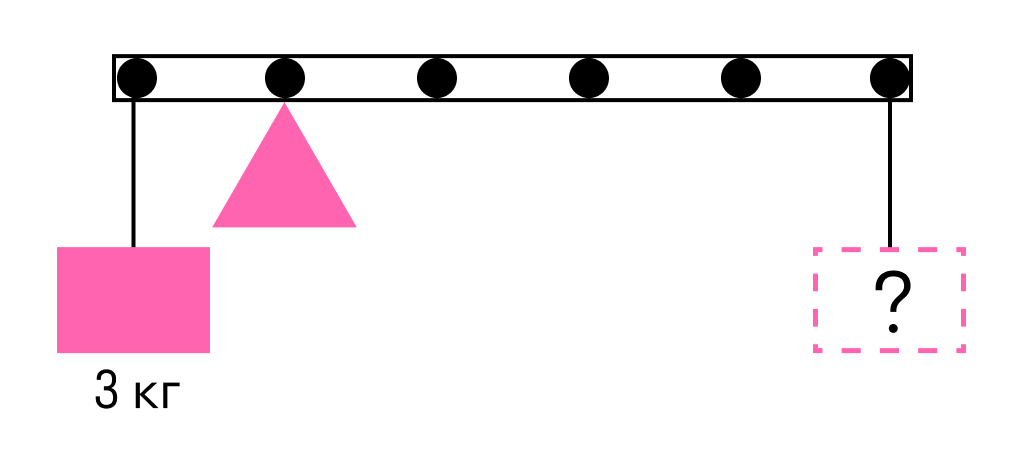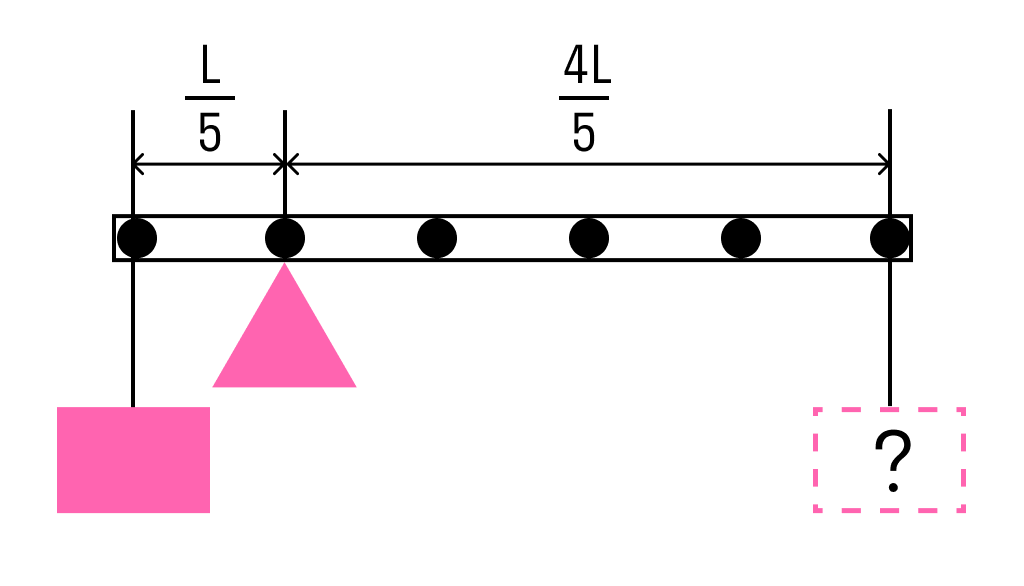механический момент в чем измеряется

Статика. Момент силы.

Момент силы вычисляют при помощи формулы:

Плечо силы – это самое короткое расстояние от линии действия силы до оси вращения тела. На рисунке ниже изображено твердое тело, которое может вращаться вокруг оси. Ось вращения этого тела является перпендикулярной к плоскости рисунка и проходит через точку, которая обозначена как буква О. Пле­чом силы F_t здесь оказывается расстояние l, от оси вращения до линии действия силы. Определяют его таким образом. Первым шагом проводят линию действия силы, далее из т. О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра оказывается плечом данной силы.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу необходимо приложить, чтобы получить желаемый результат, то есть один и тот же момент силы (см. рис. выше). Именно поэтому открыть дверь, толкая ее возле петель, намного сложнее, чем берясь за ручку, а гайку отвернуть намного легче длинным, чем коротким гаечным ключом.

За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н · м).

Правило моментов.

Твердое тело, которое может вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М₁ вращающей его по часовой стрелке, равняется моменту силы М₂, которая вращает его против часовой стрелки:

Момент силы принято считать положительным, если тело вращается по часовой стрелке, и от­рицательным, если — против.

Правило моментов есть следствие одной из теорем механики, которая была сформулирована французским ученым П. Вариньоном в 1687 г.

Пара сил.

Если на тело действуют 2 равные и противоположно направленные силы, которые не лежат на одной прямой, то такое тело не находится в равновесии, так как результирующий момент этих сил относительно любой оси не равняется нулю, так как обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена «свободному телу, то оно будет вращаться вокруг оси. проходящей через центр тяжести тела, рисунке б.

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние l между силами, которое называется плечом пары, независимо от того, на какие отрезки l, и разделяет положение оси плечо пары:

.

Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи­тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме нить действием одной пары сил с тем же моментом.

Источник

Момент силы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

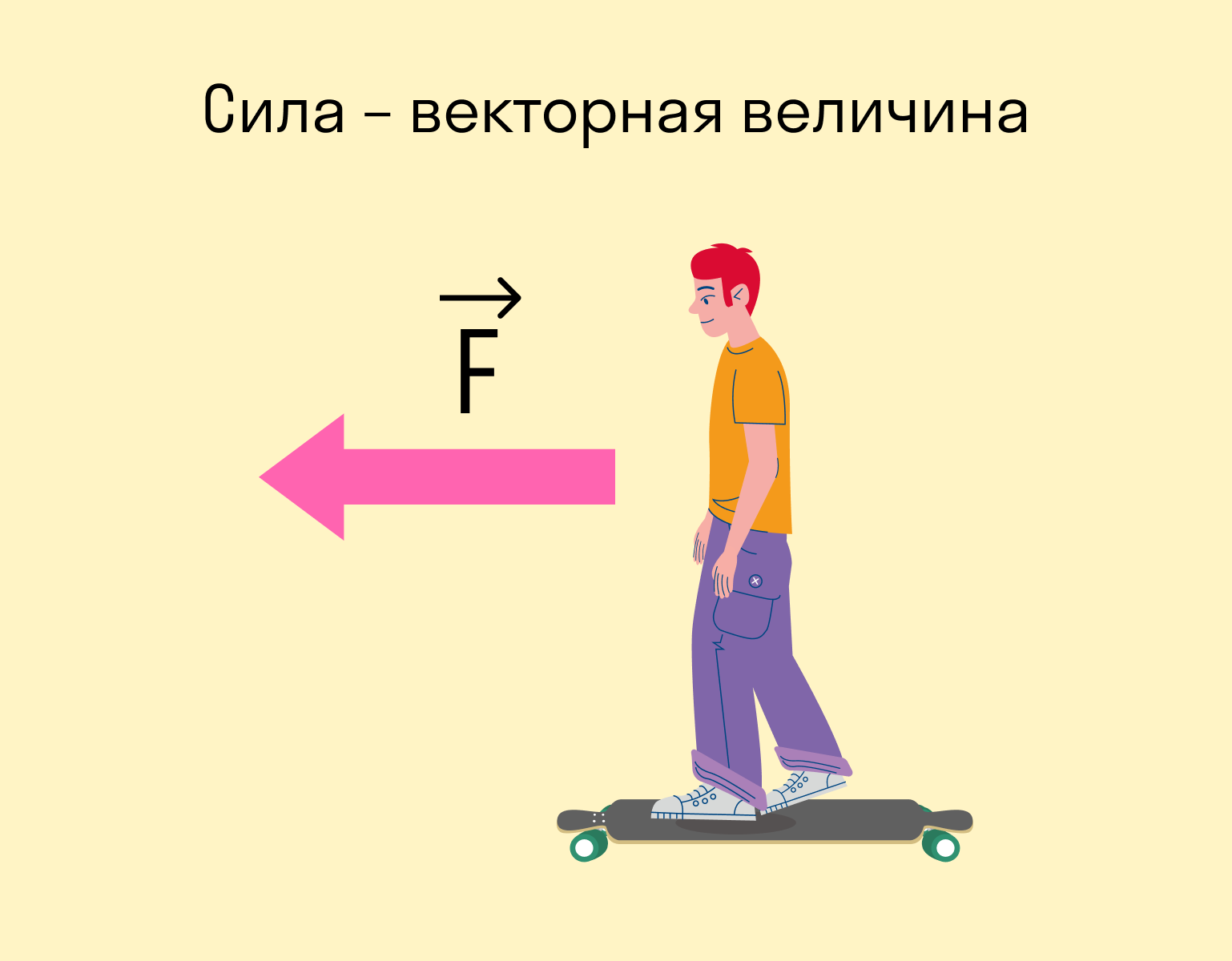
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.

Попробуйте курсы подготовки к ЕГЭ по физике с опытным преподавателем в онлайн-школе Skysmart!

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

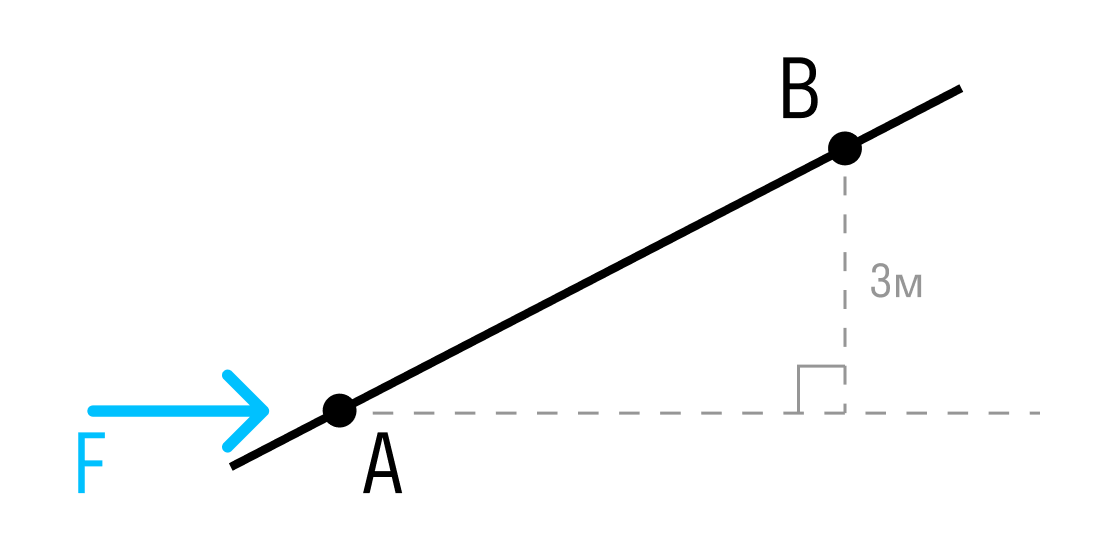
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M1 + M2 +. + Mn = M’1 + M’2 +. + M’n

M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

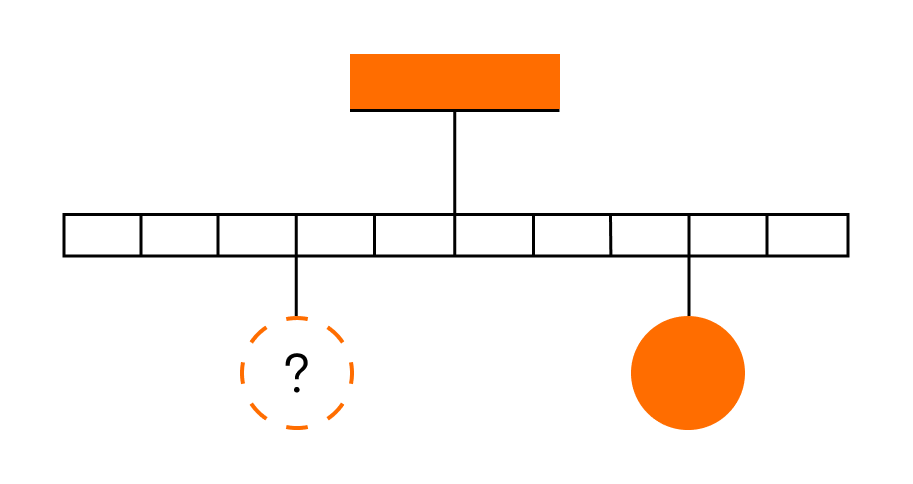
К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

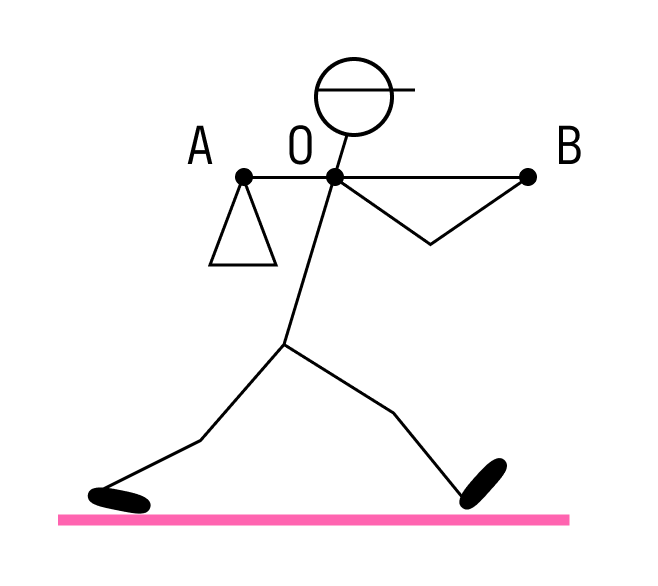
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

Задача 3

Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

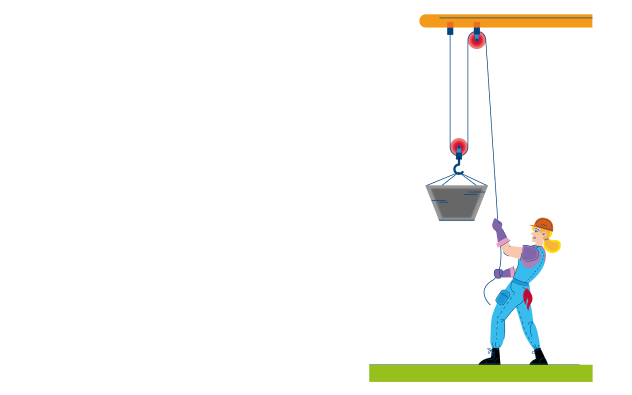
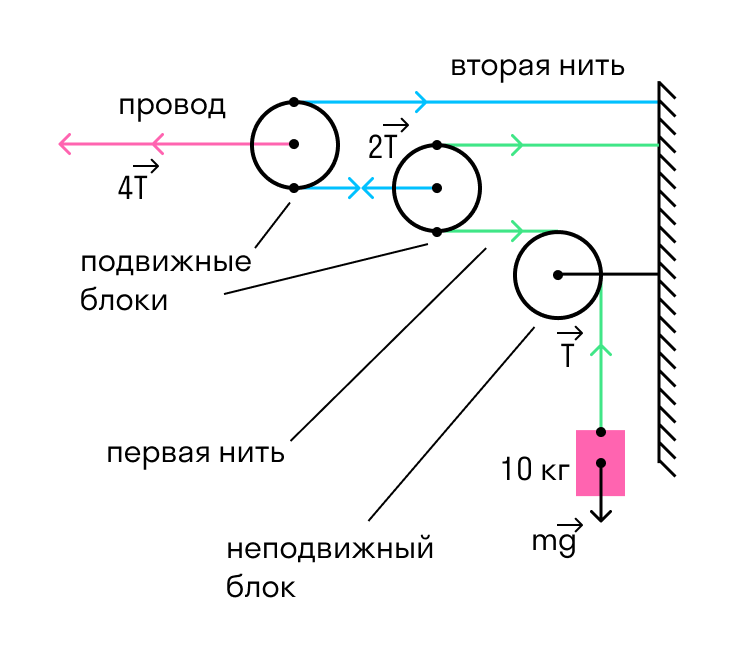
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Источник

Момент силы, формулы

Момент силы – это характеристика вращательного воздействия силы на объект. Момент силы рассчитывают, как векторное произведение вектора силы и радиус-вектора, опущенного от центра вращения до точки, к которой приложена сила.

При этом понятия «крутящий» и «вращающий» нельзя отождествлять, потому что технически вращающим моментом принято считать внешнее усилие, которое прикладывается к телу, а крутящий момент обозначает внутреннее усилие, появляющееся в теле при нагрузке. Данное понятие применимо при расчете сопротивления материалов.

Основные понятия

Не нашли что искали?

Просто напиши и мы поможем

Момент силы – это вращающая сила. По международной системе СИ единицей измерения момента вращающей силы есть ньютон-метр. Архимед при работе с рычагами отмечал, что моментом силы также считается момент пары сил.

На сегодняшний день момент силы измеряют при помощи оптических, индуктивных и тензометрических приборов нагрузки.

Формулы для нахождения момента силы

Данная формула позволяет определить только значение момента силы, но не его направление. Когда сила перпендикулярна вектору \(r ⃗,\) то момент рычага равняется расстоянию от центра вращения до точки действия силы, а момент силы имеет наибольшее значение:
\(\vec=\vec\vec\)

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Если сила воздействует на определённом расстоянии, это значит, что она делает механическую работу. Момент силы тоже делает работу, выполняя действие через угловое расстояние.
\(P = \vec \omega\)
где \(P\) – мощность, Ватт;
\(\vec\) – момент силы, ньютон-метр;
\(ω\) – угловая скорость, радиан/секунда.

Момент нескольких сил

Если тело закрепить на оси, то под воздействием пары сил оно будет вращаться вокруг этой оси. Если же пару сил приложить к свободному телу, то его вращение будет вокруг оси, проходящей через его центр тяжести.

Если равнодействующая момента нескольких сил равняется нулю, то он будет одинаковым по отношению ко всем параллельным между собой осям. Поэтому действие на объект данных сил можно заменить воздействием одной пары сил с таким же моментом.

Источник

Конвертер величин

Конвертер момента силы

Ускорение

Подробнее о моменте силы и терминологии

Общие сведения

Момент силы — это физическая величина, характеризующая насколько сила, приложенная к телу, вызывает вращение тела вокруг оси. В английском и некоторых других языках это явление называют разными словами, в зависимости от контекста. Поскольку эта статья написана для сайта переводчиков, мы немного поговорим о терминологии в других языках. Величина момента силы равна векторному произведению силы, приложенной к телу на вычисленное по перпендикуляру расстояние между осью вращения и точкой приложения силы, которая вызывает вращение. В английском языке для момента силы используют два термина, момент силы (moment of force) и отдельный термин, torque. Английский термин torque используют для обозначения физической величины, которую измеряют так же, как и момент силы (в английском), но только в контексте, в котором сила, ответственная за это свойство, обязательно вызывает вращение тела. Эту величину также измеряют, умножив силу на расстояние между осью вращения и точкой приложения силы. В русском языке термину «torque» соответствуют термины «вращающий момент» и «вращательный момент», которые являются синонимами. Русский термин «крутящий момент» относится к внутренним усилиям, возникающим в объектах под действием приложенных к ним нагрузок. Этому термину соответствуют английские термины «torsional movement», «torque effect», «torsional shear» и некоторые другие.

Как уже упоминалось выше, в этой статье мы уделяем много внимания контексту, в котором используется тот или иной английский термин. Наша задача — объяснить разницу, чтобы помочь читателю, если он в будущем столкнется с этими терминами в английском тексте. Самое главное, что следует помнить — оба термина, момент силы и torque, используют для одной и той же физической величины, но в разных контекстах. Во многих языках, как и в русском, используют только один термин. Ниже рассмотрим в каком же контексте используют каждый из этих терминов.

Терминология в английском языке

Как мы уже упоминали выше, английские термины «момент силы» и «torque» используют для одного и того же понятия, но в разных контекстах. В этом разделе обсудим, когда в английском наиболее часто используют термин «момент силы» и почти не используют «torque». Часто о понятии «torque» говорят в контексте, когда сила, действующая на тело вызывает изменение углового ускорения тела. С другой стороны, когда в английском языке говорят о моменте силы, то сила, действующая на тело не обязательно вызывает такое ускорение. То есть, «torque» — это частный пример момента силы, но не наоборот. Можно также сказать, что «torque» — это момент силы, но момент силы — не «torque».

Ниже рассмотрим несколько примеров. Стоит еще раз напомнить, что разница в использовании этих двух терминов зависит от контекста, но используют их для одного и того же физического явления. Нередко оба эти термина используют попеременно.

Чтобы понять, что такое момент силы, рассмотрим вначале, что такое момент в общем. Момент — это интенсивность, с которой сила действует на тело на определенном расстоянии относительно тела. Величина момента силы зависит от величины силы, которая действует на тело, и от расстояния от точки приложения силы до точки на теле. Как мы увидели из определения выше, эта точка часто находится на оси вращения.

Момент силы пропорционален силе и радиусу. Это значит, что если сила приложена к телу на определенном расстоянии от оси вращения, то вращательное действие этой силы умножается на радиус, то есть чем дальше от оси вращения приложена сила, тем более вращающее действие она оказывает на тело. Это принцип используется в системах рычагов, шестерней и блоков, чтобы получить выигрыш в силе. В этом контексте чаще всего говорят о моменте силы и о его использовании в различных системах, например в системах рычагов. Примеры работы рычагов показаны в статье «Подробнее о вращающем моменте». Стоит заметить, что в этой статье мы в основном обсуждаем вращающий момент, что соответствует английскому термину «torque».

Иногда понятия момент силы и вращающий момент различают с помощью понятия «пары сил». Пара сил — это две силы одинаковой величины, действующие в противоположном направлении. Эти силы вызывают вращение тела, и их векторная сумма равна нулю. То есть, термин «момент силы» используют в более общем контексте, чем вращающий момент.

В некоторых случаях термин «вращающий момент» используют, когда тело вращается, в то время как термин «момент силы» используют, когда тело не вращается, например, если речь идет об опорных балках и других конструктивных элементах зданий в строительстве. В таких системах концы балки либо жестко закреплены (жесткая заделка), либо крепление позволяет балке вращаться. Во втором случае говорят, что эта балка закреплена на шарнирной опоре. Если на эту балку действует сила, например, перпендикулярно ее поверхности, то в результате образуется момент силы. Если балка не фиксирована, а прикреплена на шарнирной опоре, то она свободно движется в ответ на действующие на нее силы. Если же балка фиксирована, то в противодействие моменту силы образуется другой момент, известный как изгибающий момент. Как видно из этого примера, термины момент силы и вращающий момент различаются тем, что момент силы не обязательно изменяет угловое ускорение. В этом примере угловое ускорение не изменяется потому, что силам извне, действующим на балку, противодействуют внутренние силы.

Примеры момента силы

Хороший пример момента силы в быту — это действие на тело одновременно момента силы и изгибающего момента, о котором мы говорили выше. Момент силы часто используют в строительстве и в проектировании строительных конструкций, так как, зная момент силы, можно определить нагрузку, которую должна выдержать эта конструкция. Нагрузка включает нагрузку от собственного веса, нагрузку, вызванную внешними воздействиями (ветром, снегом, дождем, и так далее), нагрузку от мебели и нагрузку, вызванную посетителями и обитателями здания (их вес). Нагрузка, вызванная людьми и интерьером, называется в строительстве полезной нагрузкой, а нагрузка, вызванная весом самого здания и окружающей средой называется статической или постоянной нагрузкой.

Если на балку или другой конструктивный элемент действует сила, то в ответ на эту силу возникает изгибающий момент, под действием которого некоторые части этой балки сжимаются, в то время как другие, наоборот, растягиваются. Представим, к примеру, балку, на которую действует сила, направленная вниз и приложенная по центру. Под воздействием этой силы балка принимает вогнутую форму. Верхняя часть балки, на которую действует сила, сжимается под воздействием этой силы, в то время как нижняя, наоборот, растягивается. Если нагрузка больше, чем этот материал может выдержать, то балка разрушается.

Наибольшая нагрузка — на самый верхний и самый нижний слои балки, поэтому в строительстве и при проектировании сооружений эти слои часто укрепляют. Хороший пример — использование двутавровых конструкций. Двутавр — конструктивный элемент с поперечным сечением в форме буквы Н или латинской буквы “ I” с верхней и нижней засечками (поэтому английском языке используют термин I-beam, Такая форма очень экономична, так как она позволяет упрочнить самые слабые части балки, используя при этом наименьшее количество материала. Чаще всего двутавровые балки сделаны из стали, но для прочной балки двутавровой конструкции вполне можно использовать и другие материалы. На YouTube можно найти видеосюжеты испытания двутавровых балок, сделанных из материалов, менее прочных, чем сталь, например из пенопласта и фанеры (нужно искать plywood beam test). Двутавровые балки из фанеры и древесностружечных плит появились на российском рынке стройматериалов относительно недавно, хотя они давно и очень широко применяются при строительстве каркасных домов в Северной Америке.

Если на конструкцию действует изгибающий момент, то двутавровые балки — решение проблем, связанных с прочностью. Двутавровые балки также используют в конструкциях, которые подвергаются напряжению сдвига. Края двутавровой балки противодействуют изгибающему моменту, в то время как центральная опора противостоит напряжению сдвига. Несмотря на ее достоинства, двутавровая балка не может противостоять крутящим нагрузкам. Чтобы уменьшить эту нагрузку на поверхность конструкции, ее делают круглой и полируют поверхность, чтобы предотвратить скопление нагрузки в точках с неровной поверхностью. Увеличение диаметра и изготовление такой конструкции полой внутри может помочь уменьшить ее вес.

Заключение

В это статье мы рассмотрели, чем отличаются термины «момент силы» и «вращающий момент», а также английские термины «moment of force» и «torque», и увидели несколько примеров момента силы. В основном мы говорили о случаях, когда момент силы создает проблемы в строительстве, но часто бывает наоборот и момент силы приносит пользу. Примеры использования момента силы на практике — в статье «Подробнее о вращающем моменте». Стоит также упомянуть, что разница в терминологии в английском языке чаще всего значительна в американском и британском машиностроении и строительстве, в то время как в физике эти термины часто взаимозаменяемы.

Источник