множество значений функции что это
Инструменты пользователя
Инструменты сайта
Боковая панель
Математика:
Контакты
Содержание
Нахождение множества значений функции
Обозначения
Способы нахождения областей значений функций.
Рассмотрим некоторые из них.
Используя производную
Общий подход к нахождению множества значений непрерывной функции f(x) заключается в нахождении наибольшего и наименьшего значения функции f(x) в области ее определения (или в доказательстве того, что одно из них или оба не существуют).
В случае, если нужно найти множества значений функции на отрезке:
Если областью определения функции является интервал, то используется та же схема, но вместо значений на концах используются пределы функции при стремлении аргумента к концам интервала. Значения пределов из не входят в множество значений.
Метод границ/оценок
Суть состоит в оценке непрерывной функции снизу и сверху и в доказательстве достижения функцией нижней и верхней границы оценок. При этом совпадение множества значений функции с промежутком от нижней границы оценки до верхней обуславливается непрерывностью функции и отсутствием у неё других значений.
Свойства непрерывной функции
Другой вариант заключается в преобразовании функции в непрерывную монотонную, тогда используя свойства неравенств оценивают множество значений вновь полученной функции.
Последовательное нахождение значений сложных аргументов функции
Основан на последовательном отыскании множества значений промежуточных функций, из которых составлена функция
Области значений основных элементарных функций
| Функция | Множество значений |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^<2n>$ | E(y) = [0;+∞) |
| $y = x^<2n +1>$ | E(y) = (-∞;+∞) |
| $y = k/x$ | E(y) = (-∞;0)u(0;+∞) |
| $y = x^<\frac<1><2n>>$ | E(y) = [0;+∞) |
| $y = x^<\frac<1><2n+1>>$ | E(y) = (-∞;+∞) |
| $y = a^ | E(y) = (0;+∞) |
| $y = \log_ | E(y) = (-∞;+∞) |
| $y = \sin | E(y) = [-1;1] |
| $y = \cos | E(y) = [-1;1] |
| $y = <\rm tg>\, x$ | E(y) = (-∞;+∞) |
| $y = <\rm ctg>\, x$ | E(y) = (-∞;+∞) |
| $y = \arcsin | E(y) = [-π/2; π/2] |
| $y = \arccos | E(y) = [0; π] |
| $y = <\rm arctg>\, x$ | E(y) = (-π/2; π/2) |
| $y = <\rm arcctg>\, x$ | E(y) = (0; π) |
Примеры
Найдите множество значений функции:
Используя производную
НЕ используя производную
Найдите наибольшее и наименьшее значения функции:
Если решать эту задачу с помощью производных, то потребуется преодолевать препятствия, связанные с тем, что функция f(x) определена не на отрезке, а на всей числовой прямой.
Используя метод границ/оценок
Так как данная функция непрерывна на всей области определения, то множество ее значений заключено между наименьшим и наибольшим ее значением на всей области определения, если таковые существуют.
Следовательно, E(y) = [-6;6].
Используя непрерывную функцию
Решим этот пример методом последовательного нахождения значений сложных аргументов функции. Выделив полный квадрат под логарифмом, преобразуем функцию
И последовательно найдём множества значений её сложных аргументов:
Используем прием, основанный на графическом изображении функции.
После преобразований функции, имеем: y 2 + x 2 = 25, причем y ≥ 0, |x| ≤ 5.
При этих ограничениях графиком данного уравнения является верхняя полуокружность с центром в начале координат и радиусом, равным 5. Очевидно, что E(y) = [0; 5].
Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.
В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.
Начнем с базовых определений.
Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.
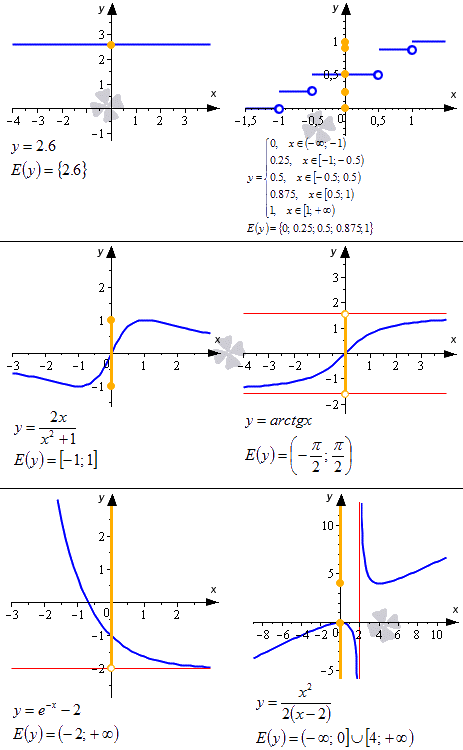
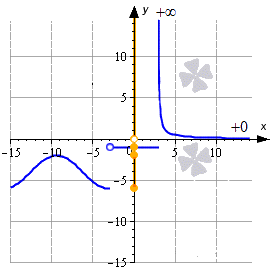
Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.
Рассмотрим основные способы нахождения области значений функции.
Возьмем задачу, в которой нужно определить область значений арксинуса.
Решение
Решение
Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.
Для определения точек экстремума надо произвести следующие вычисления:
Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.
Решение
Определяем наибольшее и наименьшее значение функции на заданном отрезке
Решение
Решение
Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.
Ответ: множество всех действительных чисел – область значений функции натурального логарифма.
Решение
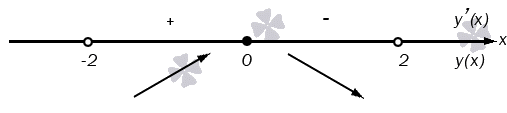
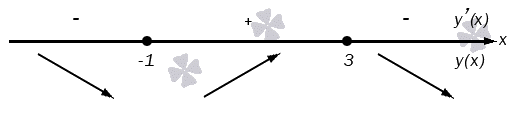
Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:
Посмотрим, как же ведет себя функция на бесконечности:
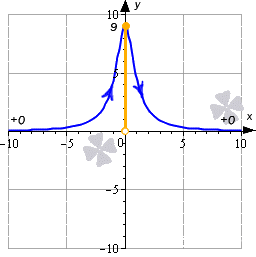
Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.
На нем видно, что областью значений функции будет интервал E ( y ) = ( 0 ; 9 ]
Ответ: E ( y ) = ( 0 ; 9 ]
А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.
Решение
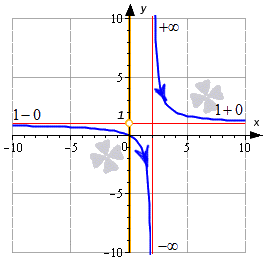
Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:
Это можно увидеть на графике:
Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.
Решение
Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.
Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.
Решение
Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.
Решение
Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.
Решение
Решение показано на графике:
Решение
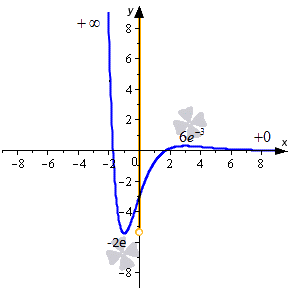
Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:
Теперь найдем соответствующие значения функции:
Посмотрим на поведение функции на бесконечности:
Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.
Параграф 2. Повторение и расширение сведений о функции.
Работу выполнил: Косярский А.А. студент группы 45.2
Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.
1. Понятие числовой функции
2. График функции
Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x
«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x
3. Возрастающие и убывающие функции
Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)
Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2)
4. Чётные и нечётные функции
Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy
Объяснение и обоснование
1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.
Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.
Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).
Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.
Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).
Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]
3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.
На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).
Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.
То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) x1 имеем
-2⋅
отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.
Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.
4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).
Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.
Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.
Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.
ВОПРОСЫ ДЛЯ КОНТРОЛЯ:
ПРИМЕРЫ РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАНИЙ
УПРАЖНЕНИЯ К ПАРАГРАФУ
5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x 5 5) y = √(x)
8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x 0
9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.
11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.
12. Обоснуйте, что заданная функция является чётной:
1) y = x 6 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x 4 )
Область определения функции
Каждая функция имеет свою собственную область определения. Целью этого материала является объяснение этого понятия и описание способов ее вычисления. Сначала мы введем основное определение, а потом на конкретных примерах покажем, как выглядит область определения основных элементарных функций (степенной, постоянной и др.) Разбирать случаи с более сложными функциями мы пока не будем.
В рамках данной статьи мы рассмотрим область определения функций, включающих в себя только одну переменную.
Понятие и обозначение области определения функции
Самое простое определение этого понятия дается в учебниках тогда, когда впервые вводится понятие функции как таковой. На этом этапе термином «область определения» обозначают множество всех возможных значений аргумента.
По мере углубления знаний о функциях определение сужается и усложняется. Так, в одном из учебников можно встретить следующую формулировку:
Используя это определение, охарактеризуем нужное нам понятие более четко:
Областью определения функции называется множество значений аргумента, на котором можно задать эту функцию.
Как найти области определения для основных элементарных функций
Прочитав определения выше, легко понять, что понятие области определения очень важно для любой функции. Это ее неотъемлемая часть, которую задают вместе с самой функцией. То есть когда мы вводим какую-либо функцию, то мы сразу указываем и область ее определения. Обычно в рамках школьного курса основные функции изучаются последовательно: сначала прямые пропорциональности, затем линейные функции, потом y = x 2 и т.д., а их области определения указываются в качестве основных свойств.
В этом пункте мы расскажем, какие области определения имеют основные элементарные функции.
Область определения постоянной функции
Область определения функции с корнем
Область определения таких функций будет зависеть от того, является ли показатель четным или нечетным числом.
Область определения степенной функции
Перечислим возможные варианты.
Поясним нашу мысль несколькими примерами.
Область определения показательной функции
Область определения логарифмической функции
Область определения тригонометрических функций
Чтобы узнать, на каком промежутке будут определены тригонометрические функции, нужно вспомнить, как именно они задаются и как называются.
Область определения тригонометрических функций
К обратным тригонометрическим относятся функции арксинуса, арккосинуса, арктангенса и арккотангенса.
Области определения основных функций в табличном виде
Чтобы запомнить или легко найти нужные нам области, правила вычисления которых мы объяснили выше, представим всю информацию в табличном виде. Не лишним будет оформить ее на отдельном листе и держать под рукой, так же, как и таблицу простых чисел, квадратов и др. Она очень пригодится при работе с функциями, пока вы не выучите ее содержимое наизусть.