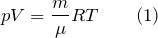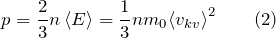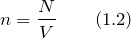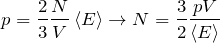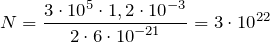модель идеального газа предполагает что
Физическая модель идеального газа. Модель идеального газа. Свойства газов
Окружающие нас природные явления и процессы являются достаточно сложными. Для их точного физического описания следует применять громоздкий математический аппарат и учитывать большое количество значимых факторов. Чтобы избежать этой проблемы, в физике используют некоторые упрощенные модели, которые значительно облегчают математический анализ процесса, но практически не влияют на точность его описания. Одной из них является модель идеального газа. Рассмотрим ее в статье подробнее.
Понятие о газе идеальном

Во-первых, речь идет о материальных точках как объектах, составляющих идеальный газ. Это означает, что его молекулы и атомы не обладают размером, но имеют определенную массу. Это смелое приближение можно сделать с учетом того, что во всех реальных газах при невысоких показателях давления и больших температурах расстояние между молекулами намного превышает их линейные размеры.
Во-вторых, молекулы в идеальном газе должны не взаимодействовать друг с другом. В действительности такие взаимодействия всегда существуют. Так, даже атомы благородных газов испытывают диполь-дипольное притяжение. Иными словами, присутствуют ван-дер-ваальсовые взаимодействия. Тем не менее по сравнению с кинетической энергией вращения и поступательного перемещения молекул эти взаимодействия настолько незначительны, что они не влияют на свойства газов. Поэтому их можно не рассматривать при решении практических задач.
Важно отметить, что не все газы, плотность в которых невелика, а температура высока, могут считаться идеальными. Помимо ван-дер-ваальсовых взаимодействий существуют другие, более сильные типы связей, например, водородные между молекулами H2O, которые приводят к грубому нарушению условий идеальности газа. По этой причине водяной пар не является идеальным газом, а воздух является им.
Физическая модель идеального газа
Эту модель можно представить следующим образом: предположим, что газовая система содержит N частиц. Это могут быть атомы и молекулы различных химических веществ и элементов. Количество частиц N велико, поэтому для его описания обычно используют единицу «моль» (1 моль соответствует числу Авогадро). Все они движутся в некотором объеме V. Движения частиц являются хаотичными и независимыми друг от друга. Каждая из них обладает определенной скоростью v и перемещается по прямой траектории.
Теоретически вероятность столкновения между частицами практически равна нулю, поскольку их размер невелик по сравнению с межчастичными расстояниями. Однако если такое столкновение происходит, то оно является абсолютно упругим. В последнем случае суммарный импульс частиц и их кинетическая энергия сохраняются.
Кинетическая теория газов
Описанная выше модель идеальных газов свойства газов определяет однозначно. Впервые эта модель была предложена Даниилом Бернулли в 1738 году.
Впоследствии ее развили до современного состояния Август Крениг, Рудольф Клаузиус, Михаил Ломоносов, Джеймс Максвелл, Людвиг Больцман, Мариан Смолуховский и другие ученые.
Кинетическая теория текучих субстанций, на основании которой построена модель идеального газа, объясняет два важных макроскопических свойства системы на основании ее микроскопического поведения:
Раскроем подробнее оба вывода кинетической теории.
Давление газа
Модель идеального газа предполагает постоянное хаотичное перемещение частиц в системе и их постоянное соударение со стенками сосуда. Каждое такое соударение считается абсолютно упругим. Масса частицы невелика (≈10-27-10-25 кг). Поэтому создать большое давление при столкновении она не может. Тем не менее количество частиц, а значит, и столкновений огромно (≈1023). Кроме того, средняя квадратичная скорость элементов составляет несколько сотен метров в секунду при комнатной температуре. Все это приводит к созданию на стенки сосуда ощутимого давления. Его можно вычислить по такой формуле:
P = N * m * vcp2 / (3 * V),
Абсолютная температура
Согласно модели идеального газа, температура однозначно определяется средней кинетической энергией молекулы или атома в изучаемой системе. Можно записать следующее выражение, которое связывает кинетическую энергию и абсолютную температуру для идеального газа:
m * vcp2 / 2 = 3 / 2 * kB * T.
Универсальное уравнение состояния
Если объединить записанные выше выражения для абсолютного давления P и абсолютной температуры T, то можно записать следующее равенство:
Универсальное уравнение впервые было выведено экспериментальным путем французским физиком Эмилем Клапейроном в XIX веке, а затем приведено к современной форме русским химиком Менделеевым, поэтому в настоящее время оно носит фамилии этих ученых.
Модель идеального газа
Определение и модель идеального газа
Моделью в физике называют упрощенную копию изучаемой настоящей системы. Она отражает самые значимые основные характеристики и свойства системы.
В модели идеального газа учитываются только основные свойства молекул, которые требуются для того, чтобы объяснить основы поведения газа. Идеальный газ напоминает реальный газ в довольно узком интервале давлений (p) и температур (T).
Главным упрощением идеального газа является предположение о том, что молекулы идеального газа не взаимодействуют на расстоянии. Кинетическая энергия движения молекул такого газа много больше, потенциальной энергии их взаимодействия. Данное упрощение ведет к уравнению состояния идеального газа:
где m – масса газа; 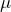
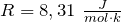
Реальные газы можно уподобить идеальному газу с достаточно высокой точностью при низких делениях, когда расстояния (в среднем) между молекулами существенно больше, чем их размеры и (или) низких температурах. В таком случае силы притяжения между молекулами можно считать ничтожно малыми, а силы отталкивания возникают на очень маленькие промежутки времени при столкновениях молекул.
Столкновения частиц идеального газа описывают при помощи законов абсолютно упругого соударения шаров. Следует отметить, что имеются в виду законы столкновения именно шаров, так как точечные частицы испытывают только лобовые столкновения, которые не могут изменять направления скоростей на разные углы. В промежутках между столкновениями молекулы идеального газа движется по прямым линиям. Законы столкновений и соударений о стенки сосудов, в которых находится газ, известны. В МКТ движение каждой молекулы идеального газа описывают при помощи законов динамики. Однако из-за того, что число молекул в газе огромно, то практически не представляется возможным написать такое число уранений.
С помощью модели идеального газа получают, например, основное уравнение молекулярно-кинетической теории (МКТ) (2). Которое показывает, что давление газа является результатом многочисленных ударов его молекул о стенки сосуда, в котором газ находится.
где 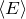
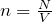
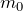
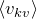
Модель идеального газа можно использовать для объяснения свойств газов. Так, горят, что газ занимает весь объем, который ему предоставляется, потому что силы взаимодействия его молекул малы, и они не способны удержать молекулы друг около друга.
Примеры решения задач
| Задание | Идеальный газ находится в сосуде объем, которого составляет 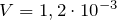 л. Давление этого газа равно л. Давление этого газа равно 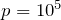 Па. Средняя кинетическая энергия, которую имеют молекулы газа Па. Средняя кинетическая энергия, которую имеют молекулы газа  Дж. Какое число молекул газа находится в сосуде? Дж. Какое число молекул газа находится в сосуде? |
| Решение | В качестве основы для решения задачи используем основное уравнение МКТ: |
Концентрация молекул (n) это:
где N — искомое число молекул газа. Подставим правую часть выражения (1.2) в (1.1), имеем:
 молекул.
молекул.| Задание | Запишите уравнение процесса, проводимого с идеальным газом, представленного на рис.1, если известно, что масса газа в этом процессе посеянная. Как изменяется давление в представленном процессе при увеличении объема? |
где A – некоторая постоянная величина. Преобразуем выражение (2.1), получим уравнение:
Рассмотрим, как изменяется давление в представленном процессе:
 . Из уравнения (2.2) следует, что с ростом объема давление уменьшается.
. Из уравнения (2.2) следует, что с ростом объема давление уменьшается.Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
Модель идеального газа, изопроцессы
Лекция № 8 Модель идеального газа. Изопроцессы.
Строение газообразных, жидких и твердых тел
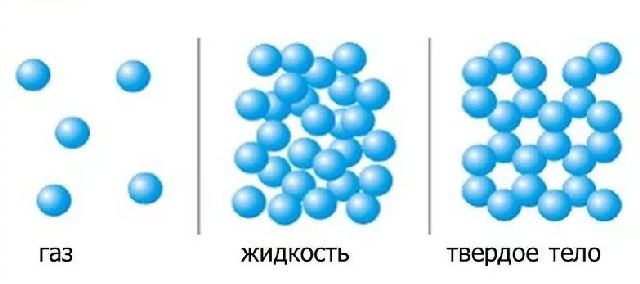
Молекулярно-кинетическая теория дает возможность понять, почему вещество может находиться в газообразном, жидком и твердом состояниях.
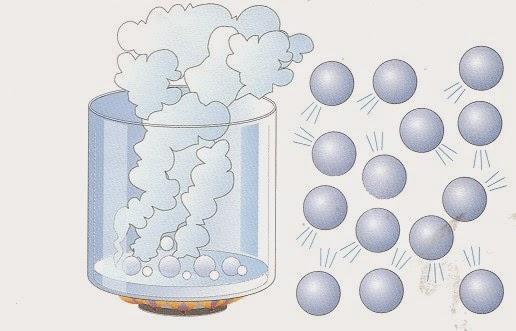
Газы. В газах расстояние между атомами или молекулами в среднем во много раз больше размеров самих молекул (рис.1). Например, при атмосферном давлении объем сосуда в десятки тысяч раз превышает объем находящихся в нем молекул.
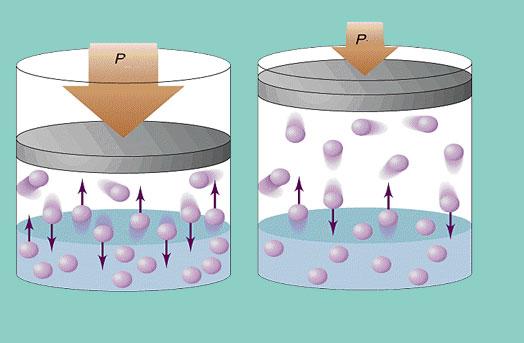
Газы легко сжимаются, при этом уменьшается среднее расстояние между молекулами, но форма молекулы не изменяется (рис.2).
Молекулы с огромными скоростями — сотни метров в секунду – движутся в пространстве. Сталкиваясь, они отскакивают друг от друга в разные стороны подобно бильярдным шарам. Слабые силы притяжения молекул газа не способны удержать их друг возле друга. Поэтому газы могут неограниченно расширяться. Они не сохраняют ни формы, ни объема. Многочисленные удары молекул о стенки сосуда создают давление газа.
Жидкости. Молекулы жидкости расположены почти вплотную друг к другу (рис.3), поэтому молекула жидкости ведет себя иначе, чем молекула газа.
В жидкостях существует так называемый ближний порядок, т. е. упорядоченное расположение молекул сохраняется на расстояниях, равных нескольким молекулярным диаметрам. Молекула колеблется около своего положения равновесия, сталкиваясь с соседними молекулами. Лишь время от времени она совершает очередной «прыжок», попадая в новое положение равновесия. В этом положении равновесия сила отталкивания равна силе притяжения, т. е. суммарная сила взаимодействия молекулы равна нулю.
Характер молекулярного движения в жидкостях, впервые установленный советским физиком Я.И.Френкелем, позволяет понять основные свойства жидкостей.
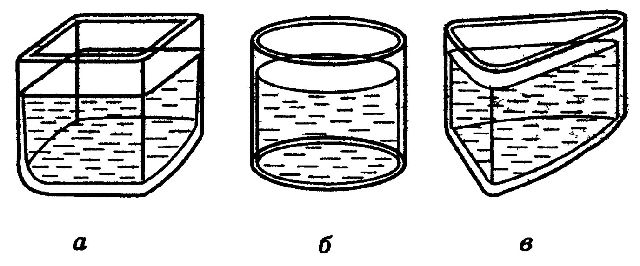
Молекулы жидкости находятся непосредственно друг возле друга. При уменьшении объема, силы отталкивания становятся, очень велики. Этим и объясняется малая сжимаемость жидкостей. Как известно, жидкости текучи, т. е. не сохраняют своей формы. Объяснить это можно так. Внешняя сила заметно не меняет числа перескоков молекул в секунду. Но перескоки молекул из одного оседлого положения в другое происходят преимущественно в направлении действия внешней силы (рис.4). Вот почему жидкость течет и принимает форму сосуда.
Твердые тела. Атомы или молекулы твердых тел, в отличие от атомов и молекул жидкостей, колеблются около определенных положений равновесия. По этой причине твердые тела сохраняют не только объем, но и форму. Потенциальная энергия взаимодействия молекул твердого тела существенно больше их кинетической энергии.
Есть еще одно важное различие между жидкостями и твердыми телами. Жидкость можно сравнить с толпой людей, где отдельные индивидуумы беспокойно толкутся на месте, а твердое тело подобно стройной когорте тех же индивидуумов, которые хотя и не стоят по стойке смирно, но выдерживают между собой в среднем определенные расстояния. Если соединить центры положений равновесия атомов или ионов твердого тела, то получится правильная пространственная решетка, называемая кристаллической.
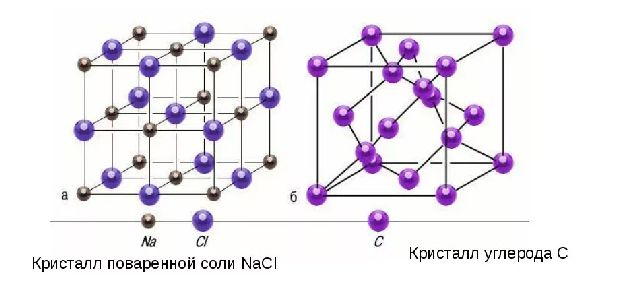
На рисунках 5 и 6 изображены кристаллические решетки поваренной соли и алмаза. Внутренний порядок в расположении атомов кристаллов приводит к правильным внешним геометрическим формам.
У газа расстояние l между молекулами много больше размеров молекул r0:l>>r0.
У жидкостей и твердых тел l≈r0. Молекулы жидкости расположены в беспорядке и время от времени перескакивают из одного оседлого положения в другое.
У кристаллических твердых тел молекулы (или атомы) расположены строго упорядоченно.
Кристаллизация — процесс фазового перехода вещества из жидкого состояния в твёрдое состояние.
Модель идеального газа
Наиболее простой теоретической моделью газа является идеальный газ. В этой модели пренебрегают размерами и взаимодействиями молекул и учитывают лишь их упругие столкновения. Более реальной является расширенная модель идеального газа, в которой молекулы представляются упругими сферами с конечным диаметром d, а взаимодействие по-прежнему учитывается только при непосредственном упругом столкновении молекул.
Установим критерий, следуя которому можно установить, когда газ можно рассматривать как идеальный. Ясно, что газ будет идеальным, если расстояние r между его молекулами такое, что силой взаимодействия между ними на этом расстоянии можно пренебречь. Как мы знаем, силы взаимодействия между молекулами быстро убывают с расстоянием r и уже на расстояниях в несколько диаметров d молекулы пренебрежимо малы. Поэтому условие идеальности газа в расширенном понимании можно записать в виде:
Из соотношений (1) и (2) следует, что критерий идеальности газа можно представить следующим образом
nd 3 3 – безразмерный параметр (3)
n = N/ѵ = (m/ν)*(Na/m) = ρNa/m (4)
где ρ = m/V — плотность газа
Выражение (4) позволяет записать критерий идеальности газа (5) в эквивалентной форме
Модель идеального газа. Давление газа.
Тема урока. Модель идеального газа. Давление газа.
развивающая : продолжить формировать у учащихся положительное отношение к самостоятельному поиску знания; продолжить развивать умения работать в парах; общеучебные знания и умения; моделировать сущность процессов, проводить мыслительный эксперимент; продолжить формирование представлений о единстве и взаимосвязи явлений природы.
воспитательная: воспитывать ответственное отношение к учебе, положительное отношение к предмету физики.
Тип урока: комбинированный на основе исследовательской деятельности.
Демонстрация : Воздушный шар; модель молекул газа и сосуд, в котором он находится (песок и пластинка из бумаги).
2. Проверка домашнего задания.
3. Мотивация учебной деятельности.
4. Изучение нового материала.
6. Домашнее задание.
Проверка домашнего задания.
1). Какими общими свойствами обладают твердые тела?
А. Собственной формой и легко изменяемым объемом.
Б. Собственной формой и объемом.
В. Собственным объемом и изменчивостью формы.
2). Чем отличается, с молекулярной точки зрения, цинк в твердом и жидком состояниях?
А. Составом молекул.
В.Расположением, взаимодействием и движением молекул.
3). Почему газы не имеют собственной формы?
А. Потому, что молекулы газа быстро движутся.
Б. Потому, что молекулы газа, практически не взаимодействуя, двигаясь свободно и хаотично, достигают всех стенок сосуда, и газ принимает его
форму.
4). Какими общими свойствами обладают жидкости?
А. Отсутствие собственной формы и объема.
Б. Обладание собственной формой и объемом.
В. Наличие у них собственного объема и текучести, следовательно, изменчивостью формы.
5). В каком состоянии вещества его молекулы сближены на расстояния, меньшие размеров самих молекул, сильно взаимодействуют и остаются на одних и тех же местах, лишь совершая около них колебания?
6).Почему газы занимают все предоставленное им пространство?
А. Потому, что молекулы газа быстро движутся.
Б. Потому, что молекулы газа, практически не взаимодействуя, двигаясь свободно и хаотично, достигают всех стенок сосуда, и газ принимает его форму.
В. Вследствие диффузии.
2. Физический диктант.
1. Относительной молекулярной массой называется…
3. Количество вещества равно отношению…
4. Постоянная Авогадро равна…
5. Молекулярной массой вещества называют…
6. Массу вещества можно рассчитать по формулам…
7. Броуновское движение – это…
8. Между атомами или молекулами существуют силы…
3. Заполнить таблицу: «Основные положения МКТ и свойства жидких, твердых и газообразных тел»
Первое положение МКТ: строение вещества
Второе положение МКТ: характер движения частиц
Третье положение МКТ: взаимодействие между частицами
Почему важно изучать газы, уметь описывать процессы, которые с ними происходят? Ответ обосновать, используя ранее полученные знания физики, собственный опыт.
Учитель побуждает учащихся дать полный ответ, используя опорные слова по методу «пресс».
Изучение нового материала.
Изучение любой области физики всегда начинается с введения некой модели, в рамках которой идет изучение в дальнейшем. Например, когда мы изучали кинематику, моделью тела была материальная точка, когда изучали планетарные движения, планеты принимались за сферы и т. д. Как вы уже догадались, модель никогда не будет соответствовать реально происходящим процессам, но часто она очень сильно приближается к этому соответствию.
Молекулярная физика, и в частности МКТ, не является исключением. Над проблемой описания модели работали многие учёные, начиная с восемнадцатого века: М. Ломоносов, Д. Джоуль, Р. Клаузиус (рис. 1). Последний, собственно, и ввёл в 1857 году модель идеального газа.
Идеальный газ – модель газа, в рамках которого молекулы и атомы газа представлены в виде очень маленьких (исчезающих размеров) упругих шариков, которые не взаимодействуют друг с другом (без непосредственного контакта), а только сталкиваются (рис. 2).
Следует отметить, что разреженный водород (под очень маленьким давлением) практически полностью удовлетворяет модели идеального газа.

Именно макропараметры измеряются измерительными приборами.
Идеальный газ – математическая модель газа, в которой предполагается, а) что, потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией;
б) суммарный объём молекул газа пренебрежимо мал. Между молекулами не действуют силы притяжения или отталкивания, соударения частиц абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями.
Упоминая об идеальном газе, мы предполагаем следующее:
— Молекулы газа очень малы и представляют собой упругие шарики.
— Молекулы этого газа двигаются беспорядочно.
Взаимодействия между молекулами газа происходят только при соударениях, а соударения считаются абсолютно упругими.
Конечно, такого газа в природе не существует. Однако данная модель очень хорошо подходит для исследования тех свойств газов, которые мы будем рассматривать в дальнейшем. Надо сказать, что разряжённый водород практически полностью соответствует модели идеального газа. Впрочем, при привычных нам температурах, таких, как комнатная температура, например, модель идеального газа достаточно хорошо описывает реальные газы, такие, как воздух.
Давление газа
Демонстрация: воздушный шар. Вопросы:
— Что вам мешает при сжатии?
— Что действует на оболочку шарика?

Конечно, манометр не может улавливать силу удара отдельных молекул. Манометр регистрирует среднюю по времени силу, которая действует на единицу площади поверхности. Если мы построим график зависимости давления от времени, то убедимся, что давление постоянно меняется (рис. 4).

Однако наблюдаются не хаотичные скачки давления, а сравнительно небольшие колебания вокруг какого-то среднего значения. Поэтому, давление оказывается вполне определенной величиной. В одном из предыдущих уроков мы убедились, что газы легко сжимаются, но при этом повышается давление. Теперь мы можем в этом ещё раз убедиться: очевидно, что если газ поместить в меньший объём, то количество соударений в единицу времени увеличится. Это увеличит среднюю силу, а, значит, давление тоже увеличится.

Но, чтобы вычислить среднее давление, необходимо знать среднюю скорость молекул. Точнее, как мы убедимся чуть позже, нам нужно знать значение не самой средней скорости, а квадрата средней скорости. Конечно же, проследить за всеми молекулами газа просто невозможно. Их очень много, все они движутся по хаотичной траектории, преодолевая несколько сотен метров в секунду. Но нас не интересует скорость отдельной молекулы. Нас интересует, к какому результату приводит движение всех молекул газа.
Можно привести простой пример. Когда повар готовит ужин для большого количества людей, он не знает, кто сколько съест. Но повар знает какое-то

среднее количество еды, которое может съесть за ужином среднестатистический человек, и, исходя из этого, рассчитывает количество еды, которое необходимо приготовить.
Точно также, нам не надо знать скорости отдельных молекул. Нам необходимо знать какое-то среднее значение скорости, и, исходя из него, производить те или иные расчеты.
Скорости движения молекул. Средняя квадратичная скорость
Кинетической энергией (в отличие от потенциальной) молекул газа не пренебрегают. Кинетическая энергия – это энергия движения, то есть она зависит от скорости, поэтому рассмотрим скорости теплового движения молекул.
Несмотря на то, что молекулы одного и того же газа являются одинаковыми, скорости у них разные. Этот факт экспериментально доказал французский физик Жан-Батист Перрен.
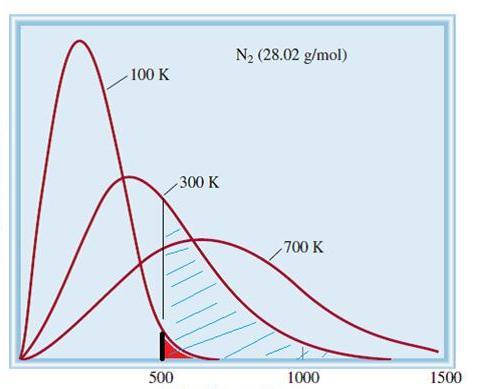
На рисунке 7 изображено распределение молекул по скоростям, так называемое распределение Максвелла. На нём видно, что существуют очень быстрые молекулы и очень медленные, но большинство молекул двигаются со средним значением скорости (выделено жёлтым).
Принято считать, что все молекулы идеального газа двигаются с одинаковой скоростью, которую назвали средней квадратичной.

Средняя квадратичная скорость – это скорость, равная корню квадратному из средней арифметической величины квадратов скоростей отдельных молекул; она несколько отличается от средней арифметической скорости молекул.

где 


К чему приводит наличие скорости у молекул газа, можно увидеть из эксперимента, для которого понадобится песок (моделирует молекулы газа) и пластинка из бумаги (моделирует сосуд, в котором находится газ). При высыпании песка пластинка под давлением песчинок отклоняется (рис. 7). Точно так же и молекулы газа оказывают давление на стенки сосуда, в котором они находятся.
Рис. 7. Отклонение пластинки под действием давления песка
Рассмотрим график зависимости давления газа на стенки сосуда от времени (Рис. 8). На нём видно, что если молекул было бы мало, то наблюдались бы отклонения, так как в какой-то момент в стенку могло бы ударить разное количество молекул, и это ощутимо поменяло бы давление. Но так как в реальности молекул огромное количество, то давление всё время остаётся постоянным.
Рис. 8. График зависимости давления газа на стенки сосуда от времени
Можно сделать вывод, что скорость – это величина, которая характеризует отдельную молекулу, а давление имеет смысл только для большого числа молекул (понятие «давление одной молекулы» совершенно бессмысленно).
Применение модели идеального газа
Модель идеального газа оказалась настолько универсальной, что физики применяют её не только для газов, подобных воздуху, но и для электронного газа в металле, для излучения электромагнитных волн и даже для звуковых колебаний в кристаллах. Теория идеального газа позволяет оценить давление и температуру внутри звёзд, результаты таких оценок близки к результатам, полученным строгими расчётами.
Назовите слова или словосочетания, которые являются «ключевыми» в данном уроке по методу «ключевые слова».
Достигнута ли цель урока? Выскажите свое мнение.
2. Ответить на вопросы:
2.1. Идеальным газом называется…
2.2. Объясните своими словами содержания понятия «идеальный газ».
2.3. Какие макропараметры, характеризующие газ, Вы знаете?
2.4. Что такое средняя квадратичная скорость?
2.5. Каким ещё способом можно продемонстрировать наличие скорости у молекул газа?
2.6. Почему с увеличением массы молекул увеличивается давление?
2.7. Почему модель идеального газа не соответствует действительности?
2.8. *Почему, говоря о микропараметрах идеального газа, мы указываем только кинетическую энергию молекулы и не указываем потенциальную?
3. Заполнить таблицу
Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский. Физика, 10 класс, М., «Просвещение», 2016. Читать §57 (с.188-190).