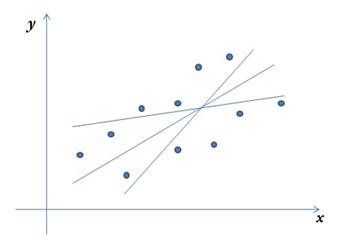
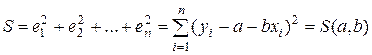модельные функции линейной модели не всегда являются чем

Параметризация линейной модели

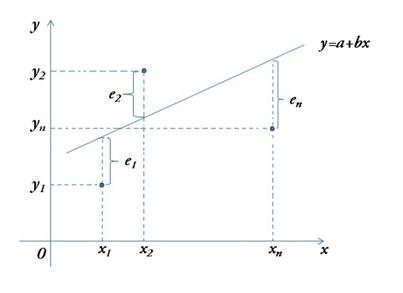
После того,как регрессионная модель специфицирована, производится ее параметризация. В случае парной линейной регрессионной модели 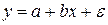речь идет о количественной оценке коэффициентов a и b. Суть параметризации парной линейной модели состоит в выборе из бесконечного множества всех прямых плоскости такой прямой, к которой точки корреляционного поля прилегают «наиболее тесным образом» (рис. 3.2). При этом в качестве меры тесноты такого прилегания могут выступать различные критерии.

Рис. 3.2. Графическая иллюстрация параметризации

парной линейной модели

Наиболее распространенным методом оценки параметров регрессииявляется метод наименьших квадратов (МНК). Этот метод является наиболее простым с вычислительной точки зрения. Здесь в качестве меры общей близости точек наблюдений от искомой прямой выбирается сумма квадратов отклонений.

Рис. 3.3. Разброс результатов наблюдений около графика

парной линейной регрессии

Суть МНК (отсюда и название метода) заключается в нахождении параметров модели, при которых минимизируется сумма квадратов отклонений эмпирических (наблюдаемых) значений , , зависимой переменной от теоретических значений , , полученных по уравнению регрессии: (при выборе линии регрессии такой критерий позволяет учитывать величину всех остатков в совокупности).

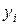
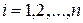
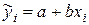
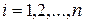
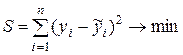
На рисунке 3.3 изображен разброс точек корреляционного поля около линии регрессии. При этом через 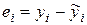обозначается разность между фактическим и теоретическим значениями зависимой переменной.

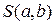
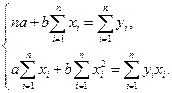
являются неизвестные параметры a и b уравнения регрессии. Исследование на экстремум данной функции проводится методами дифференциального исчисления. Приравнивая к нулю частные производные функции , приходим к системе двух линейных уравнений, из которой находятся оценки неизвестных коэффициентов a и b уравнения регрессии:

(3.2)

Решая систему, получим

, , (3.3)

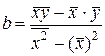
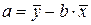
где , , , .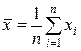

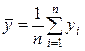
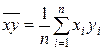
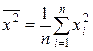
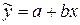
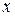
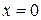
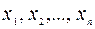
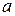
В уравнении коэффициент b при переменной x указывает, на какую величину изменится в среднем значение y при изменении фактора x на одну единицу измерения. В этом и заключается экономическая интерпретация коэффициента b. Коэффициент a формально показывает прогнозируемый уровень показателя y при значении , равном нулю. Правда, если находится достаточно далеко от выборочных значений , то буквальная интерпретация коэффициента может и не иметь ясного смысла.

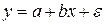
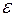
Свойства коэффициентов регрессии a и b в линейной парной модели существенным образом зависят от свойств случайной составляющей . Поэтому метод наименьших квадратов не всегда обеспечивает оптимальные свойства оценкам параметров a и b. Однако это имеет место, если линейная модель является классической.

Теорема Гаусса–Маркова. Если линейная парная модель является классической (т.е. для нее выполнены модельные предположения 1–4 пункта 3.2 данной главы), то оценки коэффициентов парной линейной регрессии, полученные с помощью МНК, являются несмещенными, состоятельными и эффективными.

Теорема Гаусса–Маркова гарантирует, что:

а) в определении линии регрессии отсутствует систематическая ошибка;

б) при возрастании числа n наблюдений дисперсия оценок параметров регрессии стремится к нулю;

в) оценки имеют наименьшую дисперсию по сравнению с любыми другими оценками.

Выполнимость модельного предположения 1 означает, что ошибки различных наблюдений поступают с разными знаками и компенсируют друг друга. Таким образом, исключается ситуация, когда ошибки систематически накапливаются с одним и тем же знаком.Проверка условия 1 отчасти может быть проведена путем анализа вида корреляционного поля. Если точки наблюдений разбросаны хаотично по отношению к линии регрессии, то условие 1 выполняется. Если же такой разброс имеет системный характер (например, в некоторой части корреляционного поля имеет место систематическое смещение точек в одну сторону от линии регрессии), то это дает основание для того, чтобы усомниться в точности вычислений либо правильности спецификации.

Требование постоянства дисперсии случайной переменной говорит о том, что все наблюдения производятся с одинаковой точностью. Поэтому в русскоязычной литературе говорят, что имеет место равноточная схема наблюдений.Выполнимость модельного предположения 2 также может быть установлена с помощью графического анализа корреляционного поля: условие 2 выполняется, если точки наблюдений расположены внутри полосы постоянной ширины, окаймляющей линию регрессии.

Отметим, что невыполнение условия 1 приводит к смещению оценок коэффициентов регрессии, а в случае невыполнения условия 2 оценки параметров могут быть неэффективными.

Последнее имеет место и при невыполнении модельных предположений 3-4, так как в этом случае коррелированность случайных членов между собой или с независимой переменной может определять систематическую тенденцию к тому, что предыдущие наблюдения будут влиять на случайный член последующих наблюдений. Условие 3 часто нарушается в динамических моделях, но практически всегда выполняется в статических.

Что касается условия 5 (предположения о нормальности), то выполнимость или невыполнимость его не оказывает существенного влияния на качество оценок параметров регрессии, но в то же время является достаточно важным. Условие 5 необходимо для проверки статистических гипотез значимости уравнения регрессии и его коэффициентов, а также для установления их доверительных интервалов. Связано это с тем, что сам аппарат проверки статистических гипотез базируется на свойствах нормально распределенных случайных величин.

Источник

Знакомьтесь, линейные модели

Машинное обучение шагает по планете. Искусственный интеллект, поскрипывая нейронными сетями, постепенно опережает людей в тех задачах, до которых успел дотянуться своими нейронами. Однако не стоит забывать и про простую модель линейной регрессии. Во-первых, потому что на ней построены многие сложные методы машинного обучения, включая нейронные сети. А, во-вторых, потому что зачастую прикладные бизнес-задачи легко, быстро и качественно решаются именно линейными моделями.
И для начала небольшой тест. Можно ли с помощью линейной модели описать:
— зависимость веса человека от его роста?
— длительность ожидания в очереди в магазине в разное время суток?
— посещаемость сайта в фазе экспоненциального роста?
— динамику во времени количества человек, ожидающих поезда на станции метро?
— вероятность, что клиент не оформит заказ на сайте в зависимости от его производительности?
Как вы догадываетесь, на все вопросы ответ будет «Да, можно». Так что линейные модели не так просты, как может показаться на первый взгляд. Поэтому давайте познакомимся с их богатым разнообразием.

Постановка задачи

В самом простом случае d = k = 1, то есть нам заданы пары чисел, например, (рост человека, вес человека) или (объем детали, вес детали) или (время ожидания в очереди, признак ухода клиента).
Чаще всего d > 1, а k = 1, то есть для каждого Y даны несколько Х, например, ((рост, возраст), вес) или ((продажи вчера, продажи позавчера, продажи позапозавчера), продажи сегодня) или ((количество поставленных задач, суммарная сложность задач), количество прогулянных работником дней под благовидным предлогом).
Бывает, что и Y тоже состоит из нескольких значений и тогда пары (X_i, Y_i) могут выглядеть, например, вот так — ((длительность физической нагрузки, уровень нагрузки, индекс массы тела, уровень тренированности), (уровень лактата в крови, длительность периода восстановления)).

И, как вы уже возможно догадались, мы вдруг делаем неожиданное предположение: наши Y не просто зависят, а линейно зависят от Х, то есть Y = b T X, где b — это параметры модели в виде вещественной матрицы размерности d ₓ k.

Однако сразу же вспомним про два важных аспекта. Во-первых, нет никаких причин, чтобы b T X вот так вот строго равнялось Y. Ведь и исходные данные мы могли измерить (и скорее всего измерили) с погрешностью. Кроме того, возможно (и даже скорее всего почти точно) мы упустили из виду какие-то факторы X, которые тоже влияют на Y. Поэтому в модели надо учесть случайную ошибку.
Во-вторых, нет никакой гарантии, что Y линейно зависят сразу напрямую от X. Ведь возможно они зависят от чего-то другого, что в свою очередь зависит от Х. Например, Y может быть равен b ∙ X 2 или b ∙ log X. А тогда почему, собственно, мы жаждем именно зависимости самого Y, а не какого-то значения, зависящего от Y, допустим, log Y = b T X.

Таким образом мы приходим к обобщенной постановке линейной задачи:
Y * = b T X * + ℇ
где X * = f(X), Y * = g(Y),
ℇ — случайная величина.

Несмотря на то, что f и g могут быть нелинейными функциями, и Y в результате может весьма нелинейно зависеть от Х, модель все равно остается линейной относительно параметров b. Именно поэтому она и называется линейной моделью.

Но это еще не вся постановка задачи

Пока мы знаем только X и Y. Правда, нашей заслуги в этом нет, поскольку они нам были даны. А как нам узнать b и ℇ?

Вспомним, что сутью модели как раз являются коэффициенты b. Ведь только ради них мы и затеяли всю эту суету. И если бы не было никаких случайных ошибок ℇ, то b можно было бы легко вычислить, решив элементарную систему из d уравнений, где d — количество факторов, то есть длина вектора X_i. Иными словами, в качестве исходных данных достаточно получить ровно d пар (X_i, Y_i), где каждый X_i состоит ровно из d значений — и точная модель готова.
Например, если исходные данные имеют вид ((размер детали, цена материала), себестоимость детали), то достаточно данных всего лишь о двух деталях, чтобы построить точную формулу себестоимости.

Но в реальной жизни так не бывает. Едва ли нам несказанно повезет, и у нас в наличии будет исчерпывающий перечень влияющих факторов, причем абсолютно точно измеренных. Поэтому в формуле нашей модели всегда будет неустранимая случайная ошибка ℇ. Причем чаще всего это будет не микроскопическая ошибка, на которую можно не обращать внимания и проигнорировать без ущерба. Нет, с ней придется считаться. И вместо двух деталей придется измерять и обсчитывать сотни и тысячи.

И все же они существуют

Разберемся с ошибками

С самими случайными ошибками ℇ все еще сложнее. Вроде мы их не знаем, и вычислить нам их не из чего, но все же они (точнее информация о них) нужна, как минимум, для точного формулирования вышеупомянутой оптимизационной задачи (а иначе как ее решать?!). Поэтому придется делать какие-то параметрические предположения.
Допустим, исходя из характера процесса, который генерирует исходные данные, мы априорно заявляем, что ℇ ∽ ℥(θ), то есть наша случайная величина ℇ описывается известным распределением ℥ с набором параметров θ, например, нормальным распределением.
Или, не зная распределения, мы можем высказать предположения о его важных свойствах. Например, что E[ℇ] = 0, то есть математическое ожидание ошибок равно нулю. Или что D[ℇ_i] = σ 2 = const, то есть дисперсии всех ошибок одинаковы и конечны.

Но зачем это всё? Ведь можно просто взять argmin от выбранного функционала и получить значение b.
Действительно можно. Вопрос лишь в качестве этого значения. Если непонятно что взять и посчитать, то получится непонятно что, а не модель.
Например, если ℇ имеет распределение Коши, то решение методом МНК даст хаотический и бессмысленный результат.
А вот, например, если одновременно выполняются условия
— E[ℇ] = 0
— E[ℇ | X] = 0, то есть ошибки не зависят от X
— D[ℇ_i] = σ 2 = const
— cov(ℇ_i, ℇ_j) = 0, где i ≠ j
то в результате расчета по МНК мы получим не просто оценку искомых параметров b, а наиболее эффективную, несмещенную и состоятельную оценку. И это все очень четко обосновано, доказано и обвязано теоремами со всех сторон.

Многообразие линейных моделей

По размерности независимой переменной (X) можно выделить однофакторные (univariable) и многофакторые (multivariable) модели.
Если зависимая переменная (Y) является скалярным значением, то имеем одинарную (univariate) модель. Когда зависимая переменная является многомерной, то есть представлена вектором, получаем множественную или общую (multivariate, general) модель.

Зависимая переменная также может содержать как исходные данные — и это будет простой моделью — так и их преобразование. Причем когда преобразованная зависимая переменная принадлежит к экспоненциальному семейству распределений, то речь уже идет о так называемой обобщенной линейной модели (GLM, generalized linear model), к которым в частности относятся нормальная, логистическая, Пуассоновская, экспоненциальная, биномиальная и многие другие модели. Обобщенные модели очень важны и удобны в использовании, поскольку для них доказаны и параметры сходимости, и качества получаемых оценок, и влияние функционалов разных видов. В идеале старайтесь свести вашу задачу к какой-нибудь GLM-модели.

И здесь уже пришло время вспомнить, что зависимая переменная может иметь очень разную природу. В частности она может быть непрерывной (вещественное число, например, вес или вероятность) или дискретной. Последняя в свою очередь может быть целым числом (например, количество клиентов или дней) или категорийным параметром, который может быть бинарным (да/нет) или мультиномиальным, причем как неупорядоченным (велосипед, автобус, метро), так и упорядоченным (оценка «хорошо», «нормально», «плохо»).
Естественно для разных типов переменных требуются разные модели. Не получится одной и той же моделью предсказывать вероятность ухода клиентов и объем их покупок, даже если влияющие факторы одни и те же.

Не будем забывать и про случайные ошибки, которые могут иметь разные распределения, оказывая тем самым сильнейшее влияние на модель и метод ее построения. Например, logit и probit модель внешне устроены совершенно одинаково, принимают одни и те же данные и предсказывают вероятность некоторого события Y при заданных X. Вот только в probit модели ошибки распределены нормально, а в logit модели имеют логистическое распределение. Естественно и результат эти модели дают разный, поэтому не стоит их путать.

Функция потерь

Регуляризация

Сложный функционал содержит регуляризацию, которая обычно представлена в виде дополнительного регуляризационного слагаемого: min ℒ(b) + λ ℱ(b), где ℒ(b) — функция потерь, ℱ(b) — регуляризационная функция, λ — параметр, задающий степень влияния регуляризации.
Регуляризация предназначена для регулирования сложности модели и ее целью является упрощение модели. Это, в частности, помогает бороться с переобучением и позволяет увеличить обобщающую способность модели.

Типичные примеры регуляризационных функций:
1. L 1 = ∑ |b|
Известная как LASSO-регуляризация (Least Absolute Shrinkage and Selection Operator), и, как несложно догадаться из названия, она позволяет снижать размерность коэффициентов, обращая некоторые из них в нули. И это весьма удобно, когда исходные данные сильно коррелированы.

2. L 2 = ∑ |b| 2
Иногда ее называют ridge-регуляризацией, и она позволяет минимизировать значения коэффициентов модели, а заодно сделать ее робастной к незначительным изменениям исходных данных. А еще она хорошо дифференцируется, а значит модель можно рассчитать аналитически.

3. L_EN = α L 1 + (1 — α) L 2
Совмещая LASSO и ridge, получаем ElasticNet, которая объединяет два мира со всеми их плюсами и минусами.

Этим, конечно, доступные виды регуляризации не ограничиваются. Хотя для линейных моделей редко требуется что-то большее.

А теперь решение

После того как мы построили функционал можно приступать к его решению. И тут есть два основных пути:
— решение в аналитическом виде
— численное решение.

Простые функционалы типа ОНК и даже ОНК с ridge-регуляризацией можно решить аналитически, то есть вывести формулу расчета искомых коэффициентов. Как правило, такие решения сразу делаются в матричном виде, например, с помощью разложений SVD или Холецкого.
Однако если данных очень много или они весьма разреженные, то даже в этих случаях лучше применять итеративные численные методы.

Обычно же аналитическое решение вообще недоступно, и приходится прибегать к численным методам и тут, конечно, мы сталкиваемся к гигантским разнообразием алгоритмов:
— стохастический градиентный спуск
— стохастический средний градиент
— метод сопряженных градиентов
— Алгоритм Бройдена — Флетчера — Гольдфарба — Шанно, а также его модификация с ограниченной памятью L-BFGS.

Источник

Что такое «линейная» модель регрессии?

Дата публикации May 29, 2019

Линейная регрессионная модель является одной из простейших моделей в области машинного обучения и статистики. При этом предположение о линейности, лежащее в основе линейной регрессии, часто понимается неточно.

Например, следующие две модели являются моделями линейной регрессии, даже линия с правой стороны не выглядит линейной.

Если это сюрприз, эта статья для вас. В этой статье я пытаюсь объяснить, какая линейность подразумевается за моделями линейной регрессии и почему линейность имеет значение.

Чтобы ответить на эти вопросы, давайте посмотрим, как линейная регрессия работает шаг за шагом, на двух простых примерах.

Пример 1: самая простая модель

Поэтому мы пытаемся смоделировать отношения междуИкса такжеYэтой очень простой линейной функцией. Ключевым моментом здесь является то, что эта функция не только линейна по отношению к входной переменнойИкс, но также линейный по параметрама, б,

Существует множество вариантов выбора функций ошибок, но одним из самых простых является тот, который называется RSS, сумма квадратов ошибок между моделями.F (X)для каждой точки данныхИкси соответствующие целевые значенияY,

С понятием функции ошибки мы можем перефразировать «определить параметрыа, бподбирая обучающие данные наиболее »как« определить параметрыа, бкоторые минимизируют функцию ошибок ».

Давайте вычислим функцию ошибки на наших данных обучения.

Как вы можете инстинктивно догадаться из приведенного выше трехмерного графика, эта функциявыпуклая функция, Оптимизация (нахождение минимума) выпуклой функции намного проще, чем общая математическая оптимизация, поскольку любой локальный минимум всегда является глобальным минимумом в выпуклой функции. (Очень простое объяснение состоит в том, что выпуклые функции имеют только одну минимальную точку, такую ​​как форма «U»). Благодаря этой характеристике выпуклых функций параметры, минимизирующие функцию, можно найти, просто решая уравнения в частных производных следующим образом.

Давайте решим наш случай.

Решая уравнения выше, мы получаема = 5/6, б = 1/2.Итак, наша первая модель (которая минимизирует RSS) получается следующим образом.

Пример 2: Простая соблазнительная модель

Теперь, для тех же точек данных, давайте подумаем о другой модели, как показано ниже.

Как видите, это не линейная функция для ввода переменнойИксбольше. Тем не менее, это все еще линейная функция для параметрова, б,

Как видно выше, уравнение выглядит очень похоже на предыдущее. (Значения коэффициентов различны, но форма уравнения та же.) Визуализация приведена ниже.

Поскольку функция ошибок второй модели также является выпуклой функцией, мы можем найти оптимальные параметры точно такой же процедурой, что и в предыдущем примере.

Решая уравнения выше, мы получаема = 61/618, b = 331/206.Итак, наша вторая модель получается как показано ниже.

Вывод: линейность позади моделей линейной регрессии

2 приведенных выше примера решаются в одной и той же (и очень простой) процедуре, даже если один из них является линейным по отношению к входной переменнойИкси один нелинейныйИкс, Общей характеристикой в ​​2 моделях является то, что обафункции линейны по параметрама, б Это линейность, принятая за моделями линейной регрессии, и это ключ к математической простоте моделей линейной регрессии.

Выше мы видели только две очень простые модели, но в целом линейность модели по ее параметрам гарантирует, что ее RSS всегда является выпуклой функцией. Это причина, почему мы можем получить оптимальные параметры, решая простые уравнения в частных производных. И именно поэтому линейность имеет значение.

Источник