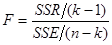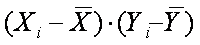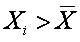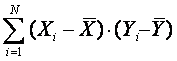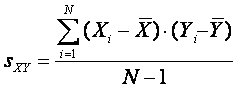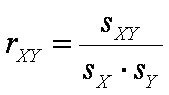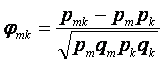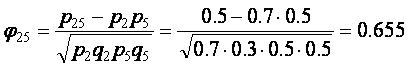корреляционная матрица что показывает
Корреляционная матрица



Корреляционная матрица показывает зависимость величин друг от друга. Элементами корреляционной матрицы являются коэффициенты корреляции величин.
Для данной задачи корреляционная матрица имеет следующий вид:
Проанализировав корреляционную матрицу, выявляем, что все предикторы являются хорошими и положительная зависимость существует со всеми предикторами, кроме Х2 (ожидаемая продолжительность жизни).
Для нас не представляет интереса брать предикторы Х2 и Х4, так как они сильно коррелированны с другими предикторами. По данной корреляционной матрице мы выбираем предикторы Х1 (детская смертность), Х3 (плодовитость женщин), Х5 (рост сельского населения), так как они в лучшей степени объясняют У (уровень рождаемости).
Всего можно построить 9 моделей с двумя предикторами, но т.к. мы не рассматриваем предикторы Х2 и Х4, то приведем модели с оставшимися предикторами и установим какая модель описывает Уровень рождаемости в большей степени.
1. Модель с предиктором Х1 (детская смертность):
Уровень рождаемости = 5,85 + 0,712 Детская смертность
Предиктор Х1 описывает Уровень рождаемости на 90,6 %.
2. Модель с предиктором Х3 (плодовитость женщин):
Предиктор Х3 описывает Уровень рождаемости всего лишь на 20%.
3. Модель с предиктором Х5 (рост сельского населения):
Уровень рождаемости = 9,35 + 2,00 Рост сельского хозяйства
Предиктор Х5 описывает Уровень рождаемости на 46,6%.
4. Модель предикторами Х1, Х3, Х5:
Уровень рождаемости = 1,58 + 0,510 Детская смертность
+ 3,86 Плодовитость женщин
+ 0,987 Рост сельского населения
Предикторы Х1, Х3, Х5 описывают Уровень рождаемости на 97,6%.
5. Модель с предикторами Х1 и Х3:
Уровень рождаемости = 4,01 + 0,687 Детская смертность
+ 1,46 Плодовитость женщин
Предикторы Х1 и Х3 описывают Уровень рождаемости на 91,1%.
6. Модель с предикторами Х1 и Х5:
Уровень рождаемости = 6,27 + 0,616 Детская смертность
+ 0,686 Рост сельского населения
Предикторы Х1 и Х5 описывают Уровень рождаемости на 94,4 %.
7. Модель с предикторами Х3 и Х5:
+ 2,19 Рост сельского населения
Предикторы Х3 и Х5 описывают Уровень рождаемости на 74,9%.
8. Модель со всеми предикторами:
— 0,413 Ожидаемая продолжительность жизни при рождении + 5,15 Плодовитость женщин
+ 0,69 Женское население
+ 0,546 Рост сельского населения
Проанализировав все наилучшие модели, приходим к выводу, что лучшей моделью является модель с тремя предикторами Х1 (детская смертность), Х3 (плодовитость женщин) и Х5 (рост сельского населении), зависимость данных предикторов с Уровнем рождаемости составляет 0,95179, 0,44751, 0,68268 соответственно. Коэффициент детерминации R 2 равен 97,6%, это значит, что эти предикторы описывают Уровень рождаемости (Y) на 97,6 %.
Хотя модель со всеми предикторами имеет самый высокий коэффициент детерминации, равный 98,3%, данная модель не может исследоваться в качестве наилучшей, так как между некоторыми предикторами существует высокая коллинеарность.
Проводя дальнейшие исследования будет использована модель с тремя предикторами (Х1, Х3 и Х5).
Проверка F теста с заданным уровнем доверия.
F-тест проверяет значимость уравнения регрессии в целом, существует ли зависимость между постоянной и переменными.
При нулевой гипотезе подтверждается, что между переменными и постоянной не существует зависимость.
Если же подтверждается первая гипотеза, то устанавливается, что между постоянной и переменными существует зависимость.
Для проверки теста понадобятся значения Fstat и Ftab.
Fstat находим по следующей формуле:
Source DF SS MS F P
Regression 3 22,4816 7,4939 244,05 0,000
Residual Error 18 0,5527 0,0307
Найдем Ftab с уровнем доверия α= 0,05
Сравнив значения Ftab и Fstat приходим в выводу, что Ftab 2 = 97,6%, т.е. Уровень рождаемости на 97,6 % объясняется Детской смертностью, Плодовитостью женщин и Ростом сельского населения.
Стандартная ошибка оценивания— это величина изменчивости, наблюдаемых значений Y, вокруг линии регрессии:
Это значит, что значения Y (Уровень рождаемости) будут отклоняться от линии регрессии на 0,175.
Корреляционная матрица
При большом числе наблюдений, когда коэффициенты корреляции необходимо последовательно вычислять из нескольких рядов числовых данных, для удобства получаемые коэффициенты сводят в таблицы, называемые корреляционными матрицами.
Корреляционная матрица — это квадратная (или прямоугольная) таблица, в которой на пересечении соответствующих строки и столбца находится коэффициент корреляции между соответствующими параметрами.
В МS Ехсеl для вычисления корреляционных матриц используется процедура Корреляция. Процедура позволяет получить корреляционную матрицу, содержащую коэффициенты корреляции между различными параметрами.
Для реализации процедуры необходимо:
1) выполнить команду СервисàАнализ данных или выбрать пункт ленточного меню ДанныеàАнализ данных;
2) в появившемся списке Инструменты анализа выбрать строку Корреляция и нажать кнопку ОК;
3) в появившемся диалоговом окне указать Входной интервал, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпускал ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши. Входной интервал должен содержать не менее двух столбцов;
4) в разделе Группировка переключатель установить в соответствии с введенными данными;
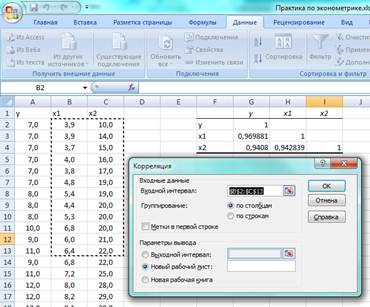
5) указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные (рис.18);
6) нажать кнопку ОК.
Рис. 18.Пример установки параметров корреляционного анализа
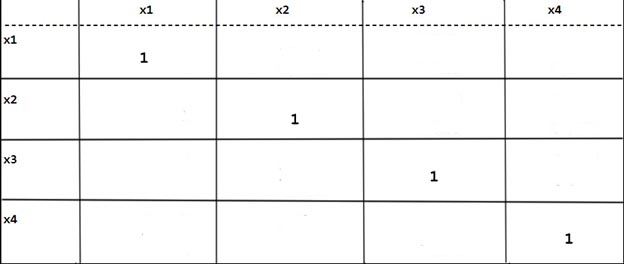
Результаты анализа, В выходной диапазон будет выведена корреляционная матрица, в которой на пересечении каждых строки и столбца находится коэффициент корреляции между соответствующими параметрами. Ячейки выходного диапазона, имеющие совпадающие координаты строк и столбцов, содержат значение 1, так как каждый столбец во входном диапазоне полностью коррелирует с самим собой.
Интерпретация результатов. Рассматривается отдельно каждый коэффициент корреляции между соответствующими параметрами. Его числовое значение оценивается по эмпирическим правилам, изложенным в разделе «Коэффициент корреляции». Отметим, что хотя в результате будет получена треугольная матрица, корреляционная матрица симметрична, и коэффициенты корреляции rij= r ji.
Пример 6.14. Имеются ежемесячные данные наблюдений за состоянием погоды и посещаемостью музеев и парков.
| Число ясных дней | Количество посетителей музея | Количество посетителей парка |
Необходимо определить, существует ли взаимосвязь между состоянием погоды и посещаемостью музеев и парков.
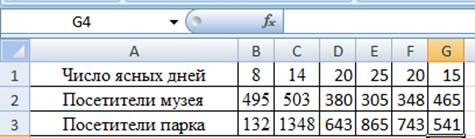
Решение.Для выполнения корреляционного анализа введите в диапазон А1:GЗ исходные данные (рис. 19).
Затем в меню Данные выберите пункт Анализ данных и далее укажите строку Корреляция. В появившемся диалоговом окне укажите Входной интервал В1:GЗ.Укажите, что данные рассматриваются по строкам. Укажите выходной диапазон. Для этого поставьте флажок в левое поле Выходной интервал и в правое поле ввода Выходной интервал введите А4 (рис. 20). Нажмите кнопку ОК.
Рис. 19 Исходные данные
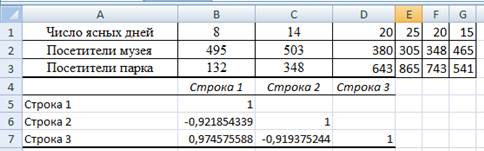
Рис. 20 Результаты вычисления корреляционной матрицы из примера 6.14
Результаты анализа. В выходном диапазоне получаем корреляционную матрицу (рис. 20).
Подразумевается, что в пустых клетках в правой верхней половине таблицы находятся те же коэффициенты корреляции, что и в нижней левой (симметрично расположенные относительно диагонали).
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Корреляционная матрица что показывает
Если две величины связаны между собой, то между ними есть корреляция. Виды корреляционной связи показаны в таблице 3.9.
Для выяснения вопроса о наличии связи между двумя величинами X и Y необходимо определить, существует ли соответствие между большими и малыми значениями X и соответствующими значениями Y или такой связи не обнаруживается. Значение каждого элемента Xi и Yi определяется величиной и знаком отклонения от среднего арифметического 11 :
Если большие значения Xi соответствуют большим значениям Yi, то это произведение будет большим и положительным, так как
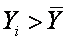
То же самое будет наблюдаться и, когда малые значения Xi будут соответствовать малым Yi, поскольку произведение отрицательных чисел будет положительным.
Если же большие значения Xi соответствуют малым значениям Yi, то это произведение будет большим и отрицательным, что будет свидетельствовать об обратной зависимости между этими величинами.
В тех случаях, когда нет систематического соответствия больших значений Xi большим или малым Yi, то знак произведения будет положительным или отрицательным для разных пар Xi и Yi. Тогда сумма
Для того, чтобы эта сумма не зависела от количества значений X и Y, ее следует поделить ее на N-1. Полученная величина sXY называется ковариацией X и Y и является мерой их связи:
Для исключения влияния стандартных отклонений на величину связи, следует поделить ковариацию sXY на стандартные отклонения sX и sY:
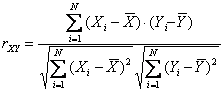
Полученная мера связи между X и Y называется коэффициентом корреляции Пирсона. Обозначение r происходит от слова регрессия. Подставив соответствующие выражения, получим формулу для коэффициента корреляции Пирсона rXY 11
Для вычислений более удобна следующая формула
Следует отметить, что в случае нелинейной связи между X и Y коэффициент корреляции может оказаться близким к нулю, даже если связь очень сильная.
Таблица 3.7.1. Типы корреляционной связи
(Гласс Дж., Стэнли Дж., 1976).
Для решения вопроса о наличии связи между заданиями теста, надо, используя данные по столбцам из бинарной матрицы, рассчитать коэффициенты корреляции Пирсона для каждой пары заданий. Для расчетов используются различные статистические программы (SPSS, STATISTICA и др.). В простейшем случае можно использовать табличный процессор Excel с вызовом функции «ПИРСОН».
pm – доля верных ответов для задания с номером m;
qm – доля неверных ответов для задания с номером m;
pk – доля верных ответов для задания k;
qk – доля неверных ответов для задания с номером k;
pmk – доля верных ответов для задания с номером m и k.
Коэффициент корреляции Пирсона, для дихотомических данных называется коэффициентом «фи». Коэффициент φmk, описывающий связь между заданиями с номерами m и k записывается следующим образом 11
Отметим, что коэффициент «фи» и коэффициент корреляции Пирсона дают в результате одно и то же значение, поскольку обе формулы эквивалентны. Рассмотрим пример вычисления коэффициента корреляции между 2-м и 5-м заданиями. Из таблицы 3.2.5 имеем: p2=0.7, q2=0.3, p5=0.5, q5=0.5. Для определения p25 надо подсчитать количество верных ответов на оба задания одновременно. Видно, что испытуемые с номерами 1-5 успешно справились с обоими заданиями (5 верных ответов). Испытуемые 6 и 7 правильно ответили на 2-е задание, но неправильно на 5-е (нет одновременно верных ответов). Испытуемые 8 и 9 не справились и со 2-м и с 5-м заданиями. Таким образом, p25 =5/10 = 0,5.
Результаты расчетов для всех заданий приведены в корреляционной матрице (таблица 3.7.2). Корреляционная матрица представляет собой квадратную матрицу размерности MxM, где M – количество заданий, симметричную относительно главной диагонали. В нашем примере матрица имеет 8 строк и столько же столбцов. Коэффициент корреляции Пирсона, скажем, между 2-м и 5-м заданиями находится на пересечении 2-й строки и 5-го столбца (0,655).
В самом последнем столбце располагается коэффициент корреляции каждого задания с тестовым баллом испытуемого (индивидуальным баллом) – rpb – точечный бисериальный коэффициент корреляции.
ТАБЛИЦА 3.7.2. Корреляционная матрица тестовых заданий.
Представление данных корреляционного анализа
Традиционно данные корреляционного анализа представляются в виде корреляционной матрицы.
Корреляционная матрица – это квадратная таблица, заголовками строк и столбцов которой являются обрабатываемые переменные.
На пересечении строк и столбцов выводится коэффициент корреляции для соответствующей пары признаков.
Корреляционная матрица обладает следующими свойствами (рис.1):
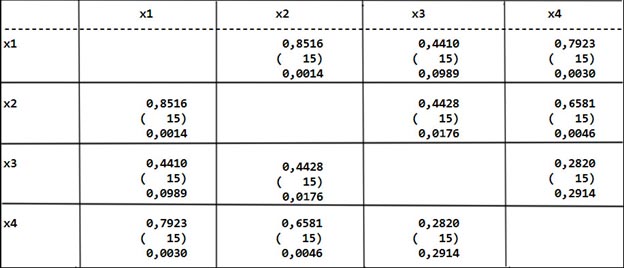
В пакете STATGRAPHICS корреляционная матрица выглядит следующим образом (рис.2), на главной диагонали цифра «1» не стоит.
На пересечении пары переменных в ячейке матрицы записываются три значения:
О представлении данных корреляционного анализа можно прочесть в книге «Компьютерная обработка данных экспериментальных исследований»
Для представления данных корреляционного анализа используется несколько способов.
ПЕРВЫЙ СПОСОБ
Значимость коэффициентов корреляции определяется на основе приведенного в заголовке таблицы критического значения коэффициента корреляции (rкрит) при определенном уровне значимости α. Также в заголовке таблицы приведен объем выборки (n). Для читающего таблицу с таким представлением информации ясно, что все коэффициенты корреляции, значения которых больше критического являются значимыми. Так корреляционная матрица представлена в книге Ан. Шалманова и Я. Ланки «Биомеханика толкания ядра».
Таблица 1 — Корреляционная матрица результатов в толкании ядра и скоростно-силовых тестах (n = 32, rкрит= 0,349, α = 0,05)