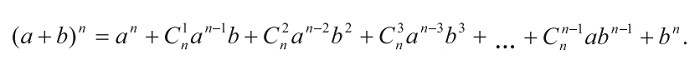квадрат бинома что это
Сокращенное умножение: правила, формулы
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
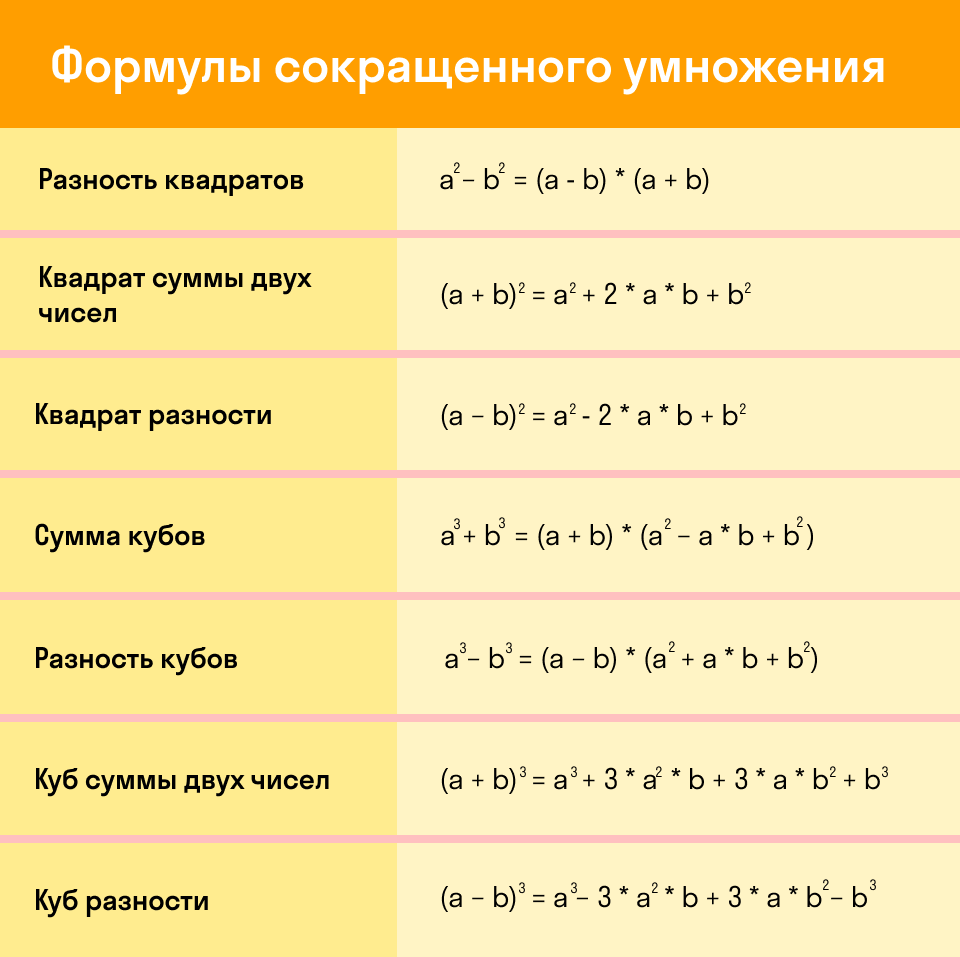
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Остальные ФСУ можно доказать аналогичным методом.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).
Для четных показателей можно записать так:
a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).
Для нечетных показателей:
a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с 3 – 8.
Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).
Задание 3
Как решаем:
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
Древние знания
Частные случаи утверждений о биномах были известны примерно с IV века до нашей эры, когда знаменитый греческий математик Евклид упомянул особый случай такой теоремы для показателя 2. Существует доказательство того, что подобие теоремы о биномах для кубов было известно уже в VI веке в Индии. Биномиальные коэффициенты, как комбинаторные величины, выражающие число способов выбора k объектов из n без замены, представляли интерес для древнеиндийских математиков.
Самое раннее упоминание этой комбинаторной проблемы встречается у индийского математика Пингала (ок. 200 г. до н. э.). В нём, кстати, содержится и метод её решения. В X веке нашей эры эту теорию прокомментировал и расширил Халаюдх, используя метод, который сейчас известен как треугольник Паскаля.
Аль-Караджи описал треугольную структуру биномиальных коэффициентов, а также представил доказательство как теоремы о биноме, так и правила треугольника Паскаля, используя раннюю форму математической индукции. Персидский поэт и математик Омар Хайям, вероятно, был знаком с формулой более высокого порядка, хотя многие из его математических работ не дошли до современных учёных.
Биноминальные разложения малых степеней были известны в математических работах XIII века Ян Хуэя и Чу Ши-Цзе. Ян Хуэй ссылается на более ранний текст Цзя Сяня, написанный в XI в., однако и эти записи в настоящее время также утрачены.
Надо сказать, что структура чисел уже была известна европейским математикам позднего ренессанса, включая:
К слову, Исааку Ньютону обычно приписывают обобщённую теорему о биномах, справедливую для любого рационального показателя.
Утверждение теоремы
Когда показатель степени равен нулю, соответствующее выражение степени принимается равным 1 и этот мультипликативный фактор часто исключается из формулы. Нередко можно видеть правую сторону уравнения, записанную в виде ( n ₒ) x n + ···. Эта формула также называется биноминальным тождеством.
Коэффициенты более высоких степеней x + y соответствуют нижним строкам паскалевского треугольника. Из расчётов можно наблюдать несколько закономерностей. В общем случае для разложения (x + y) n :
Теорема может быть применена к степеням любого бинома.
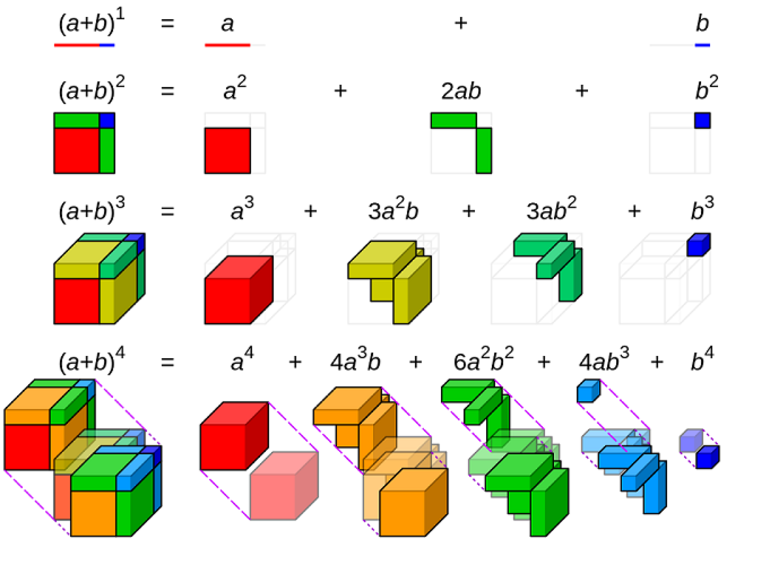
С точки зрения геометрии
Для положительных значений a и b теорема с n = 2 является геометрически очевидным фактом. Это значит, что квадрат стороны a + b может быть разделён: на квадрат стороны a и b, на два прямоугольника со сторонами a и b. При n = 3 теорема утверждает, что из куба со стороной a + b можно получить: два куба со сторонами a и b, соответственно, три прямоугольника a × a × b и столько же a × b × b.
Доказательств теоремы несколько. Для примера можно рассмотреть комбинаторное. Его алгоритм — один из самых простых. Коэффициент xy 2 в (x + y) 3 равен:
Вычисления выглядят так, потому что есть три x и y строки, а именно: xyy, yxy, yyx. Они соответствуют трём двухэлементным подмножествам <1, 2, 3>, а конкретно: <2,3>, <1,3>, <1,2>, где каждое подмножество определяет позиции y в соответствующей строке треугольника.
Доказывают биномиальную теорему либо по определению, либо по короткому комбинаторному аргументу, если ( n k) представлено как n! / k! (n-k)!.
Биномные обобщения
Около 1665 года Исаак Ньютон обобщил свою теорему, касающуюся бинома. Сделал он это для того, чтобы разрешить вещественные показатели, отличные от неотрицательных целых чисел. В этом обобщении конечная сумма заменяется бесконечным рядом. Чтобы сделать это, нужно придать смысл коэффициентам бинома с произвольным верхним индексом, что невозможно сделать с помощью обычной формулы с факториалами.
Поскольку любое значение, возведённое в ноль, равно 1, можно упростить слагаемые с нулевыми степенями. Далее, двигаясь вперёд и применяя силы, целесообразно упростить все возможные сочетания.
Короткий путь
Последняя часть должна решить формулу комбинации. Очевидный способ сделать это — применить формулу комбинации для каждой задачи. Но стоит пойти на хитрость и ускорить вычисления, используя треугольник Паскаля, образованный путём создания треугольника с тремя начальными единицами. После этого для каждой строки нужно просто написать 1 на обоих концах и найти средние числа, добавляя два значения непосредственно над ним.
Для рассматриваемой задачи нужно решить: 3 выбирает 0, 3 выбирает 1, 3 выбирает 2 и 3 выбирает 3. Все эти значения содержатся в четвёртой строке. Итак, всё, что нужно сделать, это посмотреть на четвёртый ряд треугольника и сделать выводы, сопоставив ответы. Четвёртая строка имеет значения: 1, 3, 3, 1. Поэтому надо просто заменить n на выбор k. Получается следующее: (1)8x 3 + (3)4x 2 (-3) + (3)(2x)(9) + (1)(-27).
Наконец, всё, что нужно сделать — умножить и упростить каждый термин до его простейшей формы. Стоит проверить окончательный ответ, чтобы убедиться, что полномочия каждого термина всё ещё увеличивают степень первоначального бинома.
Возведение суммы и разности двух выражений в n-ю степень
Формула для квадрата и куба бинома
Формулы для квадрата и куба бинома мы уже получили в §21 и §23 данного справочника.
$ (a+b)^2 = a^2+2ab+b^2, \qquad (a-b)^2 = a^2-2ab+b^2$
$(a+b)^3 = a^3+3a^2 b+3ab^2+b^3, \qquad (a-b)^3 = a^3-3a^2 b+3ab^2-b^3$
Формулы для четвёртой и пятой степени бинома
Выведем формулы для 4-й степени:
$ = a(a^3+3a^2 b+3ab^2+b^3 )+b(a^3+3a^2 b+3ab^2+b^3 ) =$
$= a^4+3a^3 b+3a^2 b^2+ab^3+a^3 b+3a^2 b^2+3ab^3+b^4 =$
$= a^4+4a^3 b+6a^2 b^2+4ab^3+b^4$
Для разности в 4-й степени нужно только поменять знаки при нечётных степенях b.
$(a+b)^4 = a^4+4a^3 b+6a^2 b^2+4ab^3+b^4$
$(a-b)^4 = a^4-4a^3 b+6a^2 b^2-4ab^3+b^4$
Теперь выведем формулы для 5-й степени:
$(a+b)^5 = (a+b) (a+b)^4 = a(a^4+4a^3 b+6a^2 b^2+4ab^3+b^4 )+$
$= a^5+4a^4 b+6a^3 b^2+4a^2 b^3+ab^4+a^4 b+4a^3 b^2+6a^2 b^3+4ab^4+b^5 =$
$= a^5+5a^4 b+10a^3 b^2+10a^2 b^3+5ab^4+b^5$
Для разности в 5-й степени нужно только поменять знаки при нечётных степенях b.
$(a+b)^5 = a^5+5a^4 b+10a^3 b^2+10a^2 b^3+5ab^4+b^5$
$(a-b)^5 = a^5-5a^4 b+10a^3 b^2-10a^2 b^3+5ab^4-b^5$
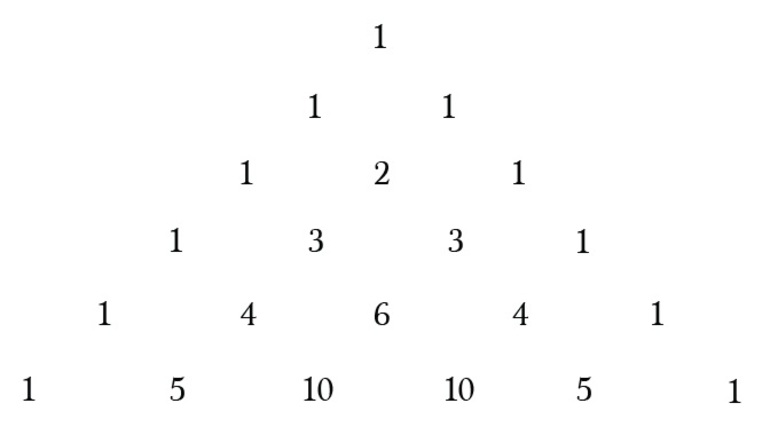
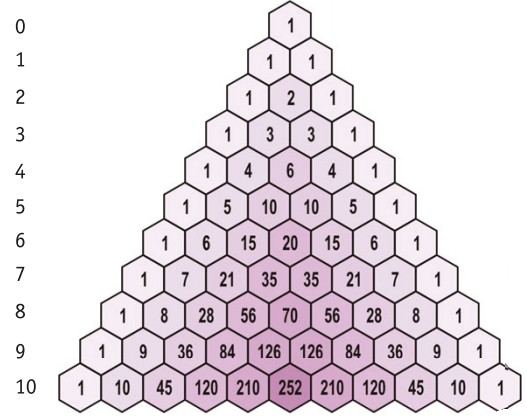
Треугольник Паскаля
Коэффициенты при членах разложения биномов постепенно становятся больше. Их рост можно представить с помощью треугольника Паскаля.
В этом треугольнике коэффициенты этажом ниже – это сумма соседних коэффициентов этажом выше; на рисунке каждая сумма обозначена знаком «+» между стрелочками.
Формула для n-ой степени бинома
Теперь для n-й степени бинома можем записать:
Формула для разности немного сложней:
Биномиальные коэффициенты играют большую роль в современной математике. В общем случае для них есть расчётная формула, которую мы выучим позже.
В общем случае для них есть расчётная формула, которую мы выучим позже (см. §36 справочника для 9 класса)
Биномиальные коэффициенты играют большую роль в современной математике. В общем случае для них есть расчётная формула, которую мы выучим позже.
Примеры
Пример 1. Представьте в виде многочлена:
Коэффициенты по модулю те же, знаки поменяются перед слагаемыми с нечётными степенями k:
$$(a+b)^7 = a^7+7a^6 b+21a^5 b^2+35a^4 b^3+35a^3 b^4+21a^2 b^5+7ab^6+b^7$$
Коэффициенты по модулю те же, знаки поменяются перед слагаемыми с нечётными степенями b:
Пример 2. Упростите выражение:
$-(x^4-4x^3 y+6x^2 y^2-4xy^3+y^4 ) = 8x^3 y+8xy^3$
$-(x^5-5x^4 y+10x^3 y^2-10x^2 y^3+5xy^4-y^5 ) = 10x^4 y+20x^2 y^3+2y^5$
$+(x^5-5x^4 y+10x^3 y^2-10x^2 y^3+5xy^4-y^5 ) = 2x^5+20x^3 y^2+10xy^4$
Бином Ньютона и треугольник Паскаля
Вот и всё. На этом можно было бы закончить, но есть одно но: большинство начинающих учеников не понимают эту формулу, не умеют пользоваться её, а уж чтобы доказать её — об этом даже речи не идёт.
Сегодня мы всё это исправим. Вы узнаете буквально всё, что нужно знать про Бином Ньютона:
Материала много, но всё будет максимально понятно и — главное — чрезвычайно полезно. Погнали!
1. Постановка задачи
Спасибо, кэп. Теперь вспомним формулы сокращённого умножения. Квадрат суммы:
Видим, что с ростом степени растёт и количество слагаемых-одночленов: их всегда на одно больше, чем степень. Но это не проблема. Проблема в другом: у этих одночленов появляются некие коэффициенты, принцип вычисления которых не ясен. Пока не ясен.
Именно для нахождения этих коэффициентов придумали бином Ньютона.
2. Бином Ньютона
Сегодня мы решим все эти проблемы. Начнём со знака суммы.
3. Знак суммы
Знак суммы — это краткая запись суммы нескольких однотипных слагаемых:
\[\sum\limits_
Более привычный формат:
То же самое с индексами:
Кроме того, полезно потренироваться и с обратным переходом — от полной записи к краткой:
В приложении к уроку — куча задач для самостоятельной тренировки.
Но вернёмся к биному Ньютона. Распишем его без знака суммы:
4. Биноминальные коэффициенты
У факториалов много интересных свойств. Чуть позже мы рассмотрим их и даже введём более корректное определение самого факториала. А пока просто потренируемся считать биноминальные коэффициенты.
Пример. На пруду плавают 5 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Пример. На пруду 150 уток. Сколькими способами можно выбрать 2 из них, чтобы покормить?
Видим, что факториалы образуют «длинные хвосты» в числителе и знаменателе, которые легко сокращаются. Однако для корректной работы с биномом Ньютона нам потребуется расширить определение факториала.
4.1. Новое определение факториала
Стандартное определение мы уже привели выше:
Но как посчитать, например, факториал нуля? И как сокращать «длинные хвосты», не расписывая факториалы? Здесь нам поможет более грамотное определение.
\[n!=\left\ < \begin
А вот ещё парочка весёлых примеров:
5. Треугольник Паскаля
\[\begin
Получили треугольник, который в народе называют «Треугольник Паскаля»: по бокам единицы, а внутри каждое число равно сумме двух ближайших, стоящих этажом выше:
И это не случайность. Перед нами важнейшее свойство биноминальных коэффициентов, которое мы оформим в виде теоремы и докажем.
Теорема. Биноминальные коэффициенты вычисляются по формуле
Распишем доказательство детально:
Заметим, что по определению факториала
\[\begin
Поэтому знаменатели биноминальных коэффициентов можно переписать:
Приведём к общему знаменателю:
Теорема доказана. Теперь мы знаем, как формируется треугольник Паскаля. Осталось доказать сам Бином Ньютона.
6. Доказательство Бинома Ньютона
Итак, нужно доказать, что
Будем доказывать по индукции.
6.1. База индукции
6.2. Индуктивное предположение
6.3. Индуктивный переход
Для этого сначала заметим, что
\[\left[ \begin
В итоге последняя сумма перепишется так:
Объединяем суммы вместе:
Такие суммы можно записать под единым знаком:
Выражение под знаком суммы легко раскладывается на множители:
Здесь в последнем шаге мы использовали свойство биноминальных коэффициентов, доказанное выше:
Или, что то же самое
Таким образом, всю сумму можно переписать более компактно, а затем внести под знак суммы первое и последнее слагаемое:
Сопоставляя исходное выражение и конечное, получим
Именно это и требовалось доказать. Следовательно, исходная формула Бинома Ньютона верна.
Бином Ньютона
В художественной литературе бином Ньютона часто упоминается, когда речь идет о чем-либо сложном. Автор этой формулы — великий физик и математик Исаак Ньютон. Дело не только в том, что формула кажется сложной. Изучение ее то включали в программу средней школы, то выводили за рамки основного курса, но в серьезных вузах экзаменаторы спрашивали и продолжают спрашивать о биноме Ньютона.
Бином Ньютона — формула разложения произвольной натуральной степени двучлена в многочлен. Каждый из нас знает наизусть формулы квадрата суммы, но при увеличении показателя степени возникают трудности с определением коэффициентов при членах многочлена. Чтобы не совершить ошибку, можно применять формулу бинома Ньютона:
Левое число — степень n, справа — значения соответствующих биномиальных коэффициентов.
Все очень просто и запоминается на всю жизнь. Кстати, самостоятельно вспомнить и вывести формулу бинома Ньютона, нарисовав треугольник Паскаля, тоже намного проще.
Ряд историков науки приписывают Паскалю авторство не только треугольника, позволяющего находить биномиальные коэффициенты, но и самой формулы бинома. Они считают, что Паскаль вывел ее несколько раньше Ньютона, а тот лишь обобщил формулу для разных показателей степеней.